On the Number of Limit Cycles in Small Perturbations of a Piecewise Linear Hamiltonian System with a Heteroclinic Loop∗
2016-06-07FengLIANGMaoanHAN
Feng LIANG Maoan HAN
1 Introduction and Main Results
A large number of problems in mechanics,electrical engineering and the theory of automatic control are described by non-smooth systems(see[1–3]and the references therein).The basic methods of the qualitative theory were established or developed by Filippov in[4].Due to the variety of the forms of non-smoothness,piecewise smooth systems exhibit not only all kinds of bifurcations that occur in smooth systems,but also complicated nonstandard bifurcation phenomenon that are unique to piecewise smooth ones including grazing(see[5–6]),sliding effects(see[7]),border collision(see[8]),etc.For limit cycle bifurcations of piecewise smooth planar systems with two regions,Han and Zhang[9]proved that linear systems can have two limit cycles near a focus of either the focus-focus,focus-parabolic or the parabolic-parabolic type(see[10]for the definition).In[11–12],the authors constructed two different classes of piecewise smooth quadratic planar systems with a focus of the focus-focus type,and showed that 5 and 9 limit cycles can respectively appear in Hopf bifurcation.In[13],Liu and Han considered a piecewise polynomial system of the form
whereare also arbitrary polynomials of degreen(n≥1).For the unperturbed system of the above,there exists a family of the periodic orbits between the origin which is an elementary center of parabolic-focus type and a compound homoclinic loop around the origin having a saddle at(1,0).We obtained that there exist systems of the form(1.1)having at leastlimit cycles forεsmall,and gained an upper boundof the number of limit cycles for this system up to the first order inε.
However,so far there have been few papers studying heteroclinic bifurcations inside the class of piecewise polynomial differential systems in the literature obtained.In this paper,we study this problem by using the first Melnikov function of piecewise near-Hamiltonian systems.
First,we recall the first-order Melnikov function for piecewise smooth near-Hamiltonian systems deduced in[13].Consider a general form of a piecewise near-Hamiltonian system on the plane

Suppose that(1.2)|ε=0has a family of periodic orbits around the origin and satisfies the following two assumptions.
Assumption(I):There exists an intervalJ=(α,β)and two pointsA(h)=(0,a(h))andA1(h)=(0,a1(h))such that forh∈J,

Assumption(II):The subsystemhas an orbital arcstarting fromA(h)and ending atA1(h)defined byH+(x,y)=h,x≥0;the subsystemhas an orbital arcstarting fromA1(h)and ending atA(h)defined by
Under assumptions(I)and(II),has a family of piecewise smooth periodic orbitsLhorientated anticlockwise with(see Figure 1).

Figure 1 The closed orbits of
Lemma 1.1(see[13])Under the assumptions(I)and(II),for the first order Melnikov function of system(1.2),we have
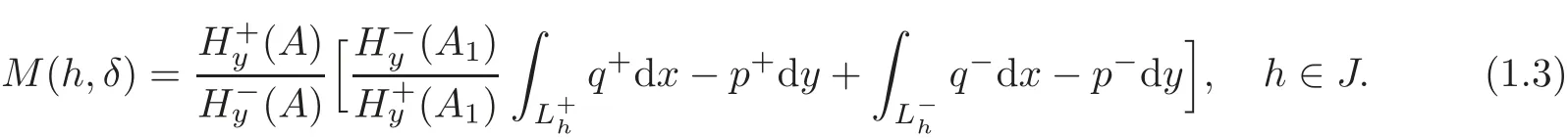
Further,if for some h0∈J,then for ε>0small,(1.2)has a unique limit cycle near Lh0.If h0is a zero of M(h)having an odd multiplicity,then for ε>0small,(1.2)has at least one limit cycle near Lh0.Also,if M(h)has at most k zeros in h on theinterval J,then(1.2)has at most k limit cycles bifurcating from the open annulus


When(1.4)and(1.5)hold,the system(1.2)has the form
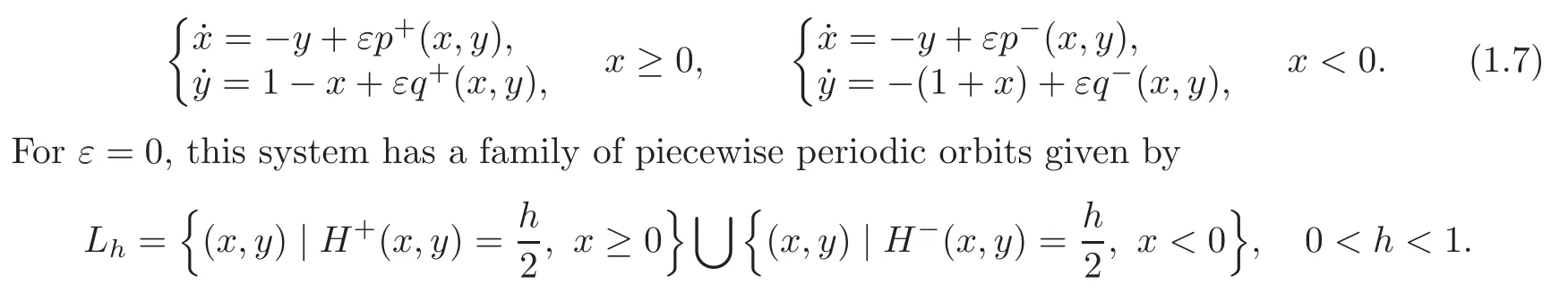
For the sake of convenience,here we useinstead ofh.The limitL0ofLhash→0 is a compound heteroclinic loop with two saddlesS1(−1,0)andS2(1,0).And ifh→1,Lhapproaches the origin which is an elementary center of parabolic-parabolic type(see[9–10]for the definition).See Figure 2.
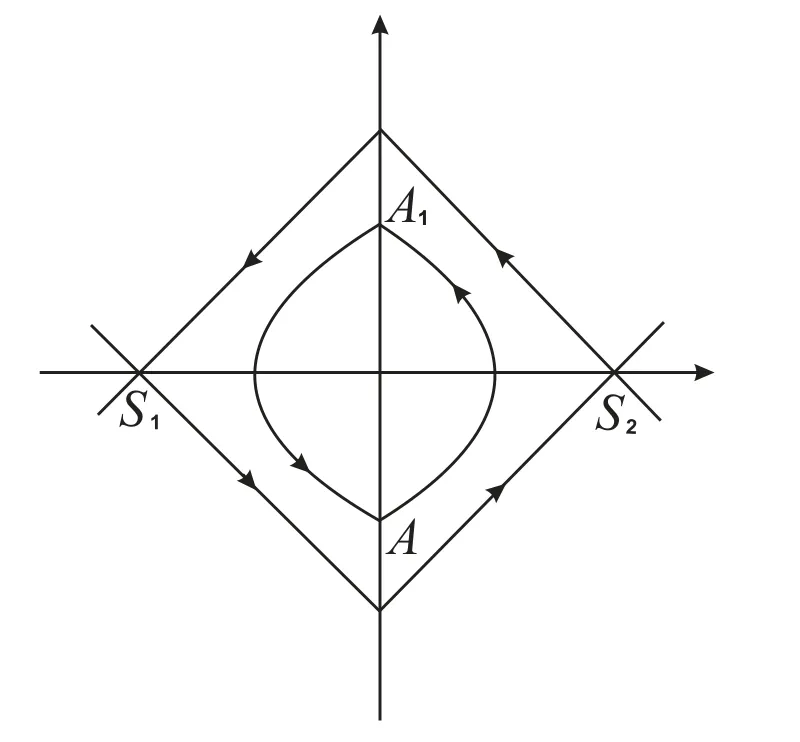
Figure 2 Phase portrait of system
Noticingfor−1<y<1,we have by Lemma 1.1 that the first-order Melnikov function of system(1.7)satisfies


LetZ(n)denote the maximal number of zeros of the non-zero functionon the open interval(0,1)for all possiblepandqsatisfying(1.6),which is the maximal number of limit cycles of(1.7)bifurcating from the periodic annulusfor all possiblepandqsatisfying(1.6).LetNHopf(n)andNheteroc(n)denote respectively the maximal number of limit cycles bifurcated in Hopf bifurcation near the origin and in heteroclinic bifurcation nearL0for all possiblepandqsatisfying(1.6).Then our main results can be stated as follows.
Theorem 1.1For any n≥1we have
(1)NHopf(n)≥n.
(2)Nheteroc(n)≥n.
Theorem 1.2For n=1,2,3,4,we have Z(n)=n.
Theorem 1.3For any n≥5we have n≤Z(n)
We conjecture thatZ(n)=nfor alln≥5.
2 Preliminary Lemmas
In this section,we give an expression of the first-order Melnikov functionin(1.8)for 0<h<1,and provide two expansions ofnear the origin and the heteroclinic loopL0respectively.By(1.8)we set for 0<h<1,


whereandare similar toμjandφiin(2.2),i=1,2.Hence,from(2.2)and(2.4)we obtain the following lemma.
Lemma 2.1For the system(1.7),the first-order Melnikov function has the following form:

whereare polynomials in u of degrees
In the following we study the expansions ofnearh=0,1.By(2.2)and(2.4),the lemma below holds immediately.
Lemma 2.2For the system(1.7),the first-order of Melnikov functionhas the following expansion:for0<h≪1

whereφ3(u)∈Cwatu=0.Then by(2.5)and Lemma 2.1,we have the following lemma.
Lemma 2.3For the system(1.7),the first order of Melnikov functionhas the following expansion:for0<1−h≪1,
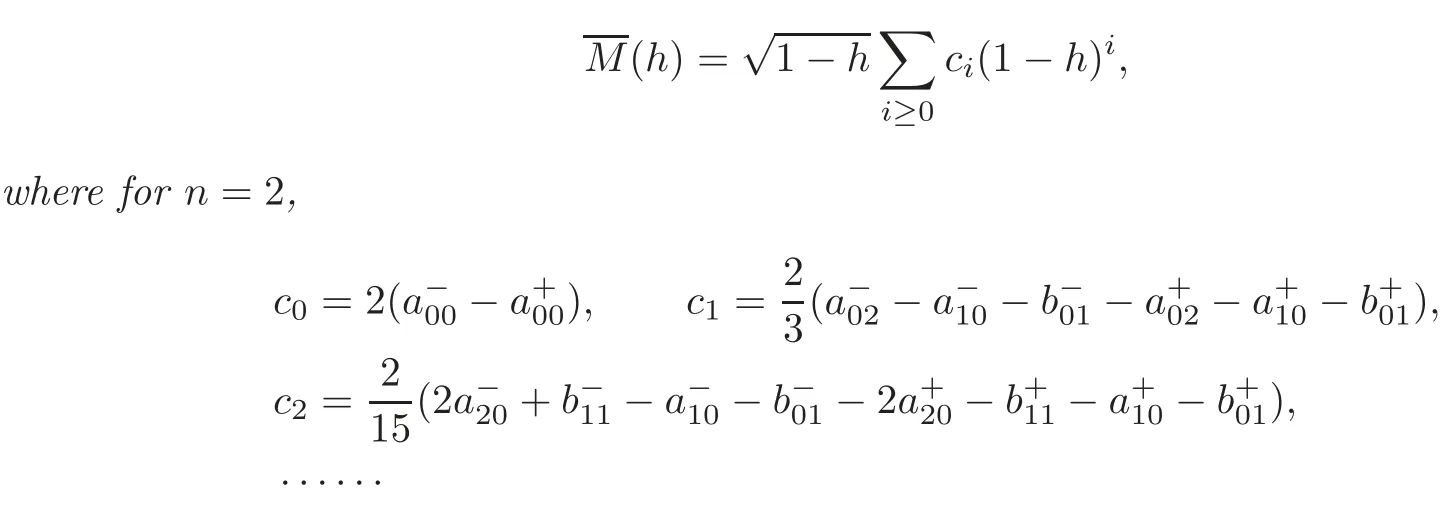
The following definition and lemma will be used in the proof of Theorem 1.2 in Section 3.
Definition 2.1(see[15])Let f0,f1,···,fm−1be analytic functions on an open interval L ofR.
(a)(f0,f1,···,fm−1)is said to be a Chebyshev system,provided that any nontrivial linear combination

3 Proof of the Main Results
Proof of Theorem 1.1(1)For simplicity,we letp±andq±in(1.6)satisfy


where p+(x,y)is independent of y.By Lemma 2.3,the first-order Melnikov function M(h)has the following expansion:Since the rank of this matrix is n+1,we can choose cj,0≤j≤n as free parameters such that 0< |c0|≪ |c1|≪ ···≪ |cn|≪ 1 and cici+1< 0,0≤ i≤ n−1.Then by(3.2),M(h)has n positive simple zeros satisfying 0<1−h≪1.Consequently,system(1.7)can have n limit cycles near the origin,which means NHopf(n)≥n.
(2)Here,we suppose that p±and q±in(1.6)satisfy


ifnis odd.Thus by(3.6),hasnpositive simple zeros nearh=0.This means that the system(1.7)can havenlimit cycles near the heteroclinic loopL0.That is,The proof ends.
Proof of Theorem 1.2 By the proof of Theorem 1.1,it suffices to prove thatforn=1,2,3 and 4.
First,forn=1,by Lemma 2.1 and(2.3),


Hence,by Lemma 2.4 and(3.9),has at most 3 zeros in the interval(0,1)for this case.It follows thatZ(3)≤3.
Forn=4,by using the same method as above,we have

Then,byM7(0)=0 andM8(0)=0,it is clear thatW[f0,f1,f2,f3,f4]<0.Thus,(f0,f1,f2,f3,f4)is also an extended complete Chebyshev system on(0,1).Therefore,by Definition 2.1(c)and(3.10),has at most 4 zeros in the interval(0,1),which yieldsZ(4)≤4.The proof ends.
Proof of Theorem 1.3 Following Theorem 1.1,we only need to proveSimilar to the method used in[19]for instance,we give the proof bellow.By(2.3)and Lemma 2.1,it follows that

AcknowledgementThe authors would like to thank the reviewers for their valuable comments and suggestions.
[1]di Bernardo,M.,Budd,C.J.,Champneys,A.R.and Kowalczyk,P.,Piecewise-Smooth Dynamical Systems,Theory and Applications,Springer-Verlag,London,2008.
[2]Andronov,A.A.,Khaikin,S.E.and Vitt,A.A.,Theory of Oscillators,Pergamon Press,Oxford,1965.
[3]Kunze,M.,Non-smooth Dynamical Systems,Springer-Verlag,Berlin,2000.
[4]Filippov,A.F.,Differential Equations with Discontinuous Righthand Sides,Kluwer Academic,Netherlands,1988.
[5]Bernardo,M.D.,Budd,C.J.and Champneys,A.R.,Grazing,skipping and sliding:Analysis of the nonsmooth dynamics of the DC/DC buck converter,Nonlinearity,11,1998,859–890.
[6]Budd,C.J.,Non-smooth dynamical systems and the grazing bifurcation,Nonlinear Mathematics and Its Applications,Cambridge Univ.Press,Cambridge,1996.
[7]Bernardo,M.D.,Kowalczyk,P.and Nordmark,A.B.,Sliding bifurcations:A novel mechanism for the sudden onset of chaos in dry friction oscillators,Internat.J.Bifur.Chaos Appl.Sci.Engrg.,13(10),2003,2935–2948.
[8]Nusse,H.E.and Yorke,J.A.,Border-collision bifurcations including “period two to period three” for piecewise smooth systems,Physica D,57(1–2),1992,39–57.
[9]Han,M.and Zhang,W.,On Hopf bifurcation in nonsmooth planar systems,J.Differential Equations,248,2010,2399–2416.
[10]Coll,B.,Gasull,A.and Prohens R.,Degenerate Hopf bifurcations in discontinuous planar systems,J.Math.Anal.Appl.,253(2),2001,671–690.
[11]Gasull,A.and Torregrosa,J.,Center-focus problem for discontinuous planar differential equations,Int.J.Bifur.Chaos,13(7),2003,1755–1765.
[12]Chen,X.and Du,Z.,Limit cycles bifurcate from centers of discontinuous quadratic systems,Comput.Math.Appl.,59(12),2010,3836–3848.
[13]Liu,X.and Han,M.,Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems,Internat.J.Bifur.Chaos Appl.Sci.Engrg.,20(5),2010,1–12.
[14]Liang,F.,Han,M.and Romanovski,V.G.,Bifurcation of limit cycles by perturbing a piecewise linear Hamiltonian system with a homoclinic loop,Nonlinear Analysis,75(11),2012,4355–4374.
[15]Karlin,S.and Studden,W.,TchebycheffSystems:With Applications in Analysis and Statistics,Interscience Publishers,New York,1966.
[16]Du,Z.and Zhang,W.,Melnikov method for homoclinic bifurcation in nonlinear impact oscillators,Comput.Math.Appl.,50(3–4),2005,445–458.
[17]Battelli,F.and Fe˘ckan,M.,Bifurcation and chaos near sliding homoclinics,J.Differential Equations,248(9),2010,2227–2262.
[18]Llibre,J.and Makhlonf,A.,Bifurcation of limit cycles from a two-dimensional center insideRn,Nonlinear Analysis,72(3–4),2010,1387–1392.
[19]Llibre,J.,Wu,H.and Yu,J.,Linear estimate for the number of limit cycles of a perturbed cubic polynomial differential system,Nonlinear Analysis,70(1),2009,419–432.
[20]Han,M.,On Hopf cyclicity of planar systems,J.Math.Anal.Appl.,245(2),2000,404–422.
[21]Han,M.,Chen,G.and Sun,C.,On the number of limit cycles in near-Hamiltonian polynomial systems,Internat.J.Bifur.Chaos Appl.Sci.Engrg.,17(6),2007,2033–2047.
[22]Wu,Y.,Cao,Y.and Han,M.,Bifurcations of limit cycles in az3-equivariant quartic planar vector field,Chaos,Solitons&Fractals,38(4),2008,1177–1186.
[23]Yang,J.and Han,M.,Limit cycle bifurcations of some Li´enard systems with a cuspidal loop and a homoclinic loop,Chaos,Solitons&Fractals,44(4–5),2011,269–289.
[24]Han,M.and Chen,J.,On the number of limit cycles in double homoclinic bifurcations,Sci.China,Ser.A,43(9),2000,914–928.
[25]Han,M.,Cyclicity of planar homoclinic loops and quadratic integrable systems,Sci.China,Ser.A,40(12),1997,1247–1258.
杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- On Unitary Invariant Weakly Complex Berwald Metrics with Vanishing Holomorphic Curvature and Closed Geodesics∗
- Witten’s D4Integrable Hierarchies Conjecture∗
- A Note on the Maximal Functions on Weighted Harmonic AN Groups
- Gröbner-Shirshov Basis for Degenerate Ringel-Hall Algebras of Type
- Fixed Point Theorems for(p,q)-Quasi-Contraction Mappings in Cone Metric Spaces
- Approximate Representation of Bergman Submodules∗
