基于逆运动学的6-UPS并联机构运动学参数辨识方法

赵海波，李巍，王一建

（中国科学院长春光学精密机械与物理研究所，长春　130033）



基于逆运动学的6-UPS并联机构运动学参数辨识方法

赵海波，李巍，王一建

（中国科学院长春光学精密机械与物理研究所，长春130033）

摘要：为了提高6-UPS并联机构的定位精度，研究了一种基于逆运动学的6-UPS并联机构运动学参数辨识方法。首先基于逆运动学建立了6-UPS并联机构的运动学参数辨识模型，然后通过Levenberg-Marquardt最小二乘法对模型进行求解，最后对该算法进行了仿真验证。结果表明该算法可以很快收敛，在测量设备没有测量误差的理想状态下，参数辨识精度达到10-10mm。在测量设备存在1μm、1″的误差状态下，参数辨识精度达到10-3mm，足以满足大部分应用场合下6-UPS的位姿精度要求。

关键词：6-UPS并联机构；逆运动学；运动学参数辨识；最小二乘法

6-UPS并联机构具有刚度大、运动精度高、动态性能优越、实时控制简易等优点，在精密定位领域有着重要应用［1，2］。位姿调节精度是6-UPS并联机构的关键指标［3］，该机构的制造和装配误差会对其定位精度造成很大影响，进而影响其工作性能。为提高6-UPS并联机构的性能，就必须减小其位姿误差，提高定位精度，对于定位精度要求极高的6-UPS并联机构，仅靠提高加工制造精度来达到其定位精度的要求，目前的加工装配水平是无法实现的。相比而言，通过参数辨识进而对误差进行补偿的方法来提高6-UPS并联机构的精度是十分可行的。

1　运动学参数辨识

运动学参数辨识，又称精度补偿，是提高并联机构精度的有效手段［4，5］。根据并联机构的机构特点，确定其参数辨识具体参数，建立参数辨识模型，利用测量工具对并联机构的位姿进行测量，构造机构位姿与参数辨识参数之间的关系方程，利用参数辨识算法进行辨识，根据辨识的结果修改控制系统的模型控制参数，进行误差补偿。

目前，并联机构的参数辨识方法按照测量方法的不同主要分为自参数辨识法和外参数辨识法两种［6］。利用自参数辨识法进行参数辨识时需要利用内部观测器获取信息，其一般需要在铰链处安装传感器［7］。这种方法在实际应用中往往受到传感器种类和尺寸的限制，不能辨识机构所有的几何参数。利用外参数辨识法进行参数辨识时需要利用外部测量工具来测量运动平台的位姿信息。该方法可以辨识并联机构所有的几何参数。6-UPS并联机构需要辨识的几何参数一共42项，参数较多，故选择外参数辨识方法，用外部测量设备测量动平台的位姿。

另外，按照运动学模型的不同，并联机构的参数辨识方法又可以分为基于正运动学的参数辨识法和基于逆运动学的参数辨识法两种。6-UPS并联机构的正运动学求解是一个迭代求解过程，算法较为复杂，耗时较长，而逆运动学求解过程则不需要迭代求解，耗时短，效率高，因此，本文决定以逆运动学算法为基础构建6-UPS并联机构的运动学辨识模型。

2　6-UPS并联机构的逆运动学

6-UPS并联机构的结构如图1所示，由六根可自由伸缩的支杆通过虎克铰和球铰将动平台和定平台连接在一起。以定平台中心为坐标原点建立定坐标系｛B｝，其z轴垂直定平台；以动平台的旋转中心为坐标原点建立动坐标系｛P｝，ri为虎克铰中心Ai在定坐标系｛B｝中的位置矢量；Pi为球铰中心Bi在动坐标系｛P｝中的位置矢量。6-UPS并联机构的逆运动学：已知动平台位姿P和机构的几何参数u，求解六支杆长度l。

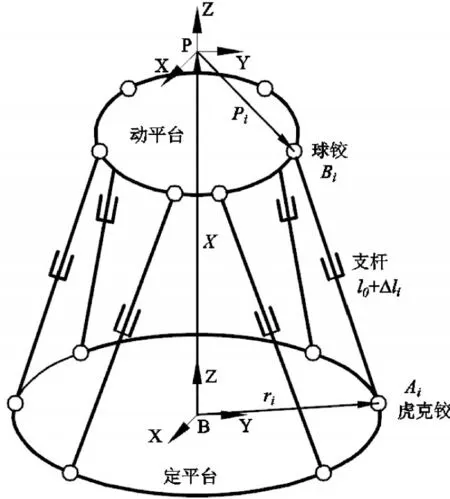
图1　6-UPS并联机构结构示意图

由图1中的矢量关系可得：

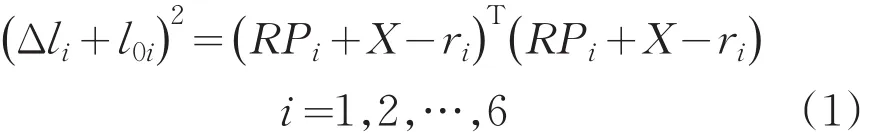
式中：

Δli-第i个支杆长度变化量；

l0i-第i个支杆在初始零位的长度；

R -坐标系｛P｝到坐标系｛B｝的旋转变换矩阵；

X -坐标系｛P｝原点在坐标系｛B｝中的位置矢量。

3　6-UPS并联机构参数辨识模型

由6-UPS并联机构的逆运动学可知，给定动平台的位姿［R，X］T，以及6-UPS并联机构的几何参数：ui=［ri，Pi，l0i］T，即可求得各个支杆长度变化量Δli，i =1，2，…，6；6-UPS并联机构的参数辨识是指已知动平台的真实位姿［Rj，Xj］T和各个支杆长度变化量Δli，j（i =1，2，…，6；j =1，2，…，m；m为测得的位姿数）情况下，求6-UPS并联机构的几何参数：ui=［ri，Pi，l0i］T，共42个参量。

3.16-UPS并联机构参数辨识模型的构建

根据式（2）所示的残差函数fi，j，可构建6-UPS并联机构参数辨识模型，即支杆长度变化量残差平方的和C：

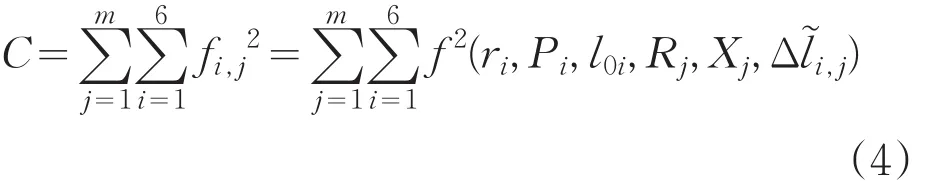
若6-UPS并联机构几何参数的辨识结果与实际值越接近，其由运动学逆解计算得到的支杆长度变化量与测得的支杆长度变化量的差值越小，支杆长度变化量残差平方的和C越接近于零，当C= 0时，辨识的机构几何参数值等于其实际值。6-UPS并联机构的参数辨识问题转化为最优化问题，即为求解使式（3）中的C值最小机构的42个几何参数。

3.26-UPS并联机构参数辨识模型的雅克比矩阵

对6-UPS并联机构的运动学逆解式（1）等式两边微分可得：

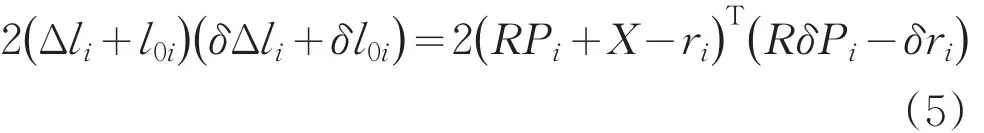
化简得：

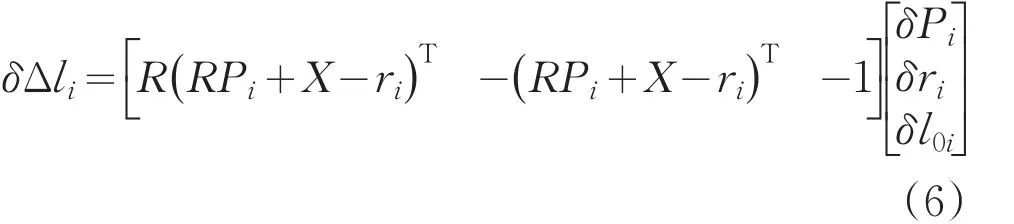
所以，6-UPS并联机构单杆参数辨识模型的雅克比矩阵为：

由单杆参数辨识模型的雅克比矩阵可得6-UPS并联机构整体参数辨识模型的雅克比矩阵：

4　参数辨识模型求解算法

由6-UPS并联机构的参数辨识模型可知，共有42个需要辨识的几何参数，而其动平台的每个位姿包含6个相互独立的变量，因此，最少需测量7组位姿，为使辨识的结果具有良好的鲁棒特性，应选取不少于20个位姿构造一个超定残差方程。具体的解法，本文选用最小二乘法［8］。最小二乘法中最常用的是Guss-Newton法，但是该方法的迭代公式中需要对矩阵求逆，容易出现奇异性导致求解失效，而且，当其探索方向与该点处的负梯度方向正交或者接近正交时，Guss-Newton法收敛速度会减慢，甚至会出现假收敛。Levenberg-Marquardt方法可以很好的解决以上问题，不会出现奇异性并且收敛速度快。

采用Levenberg-Marquardt算法求解6-UPS并联机构的参数辨识模型的步骤如下所示：

（1）选取初始几何参数u0，给定初始参数α0，放大因子β，以及允许误差ε，k =0；

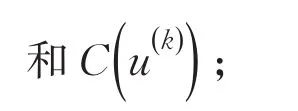
（3）检查是否满足终止准则：若C（u（k））≤ε，则终止迭代，u（k）为最终所辨识的几何参数；否则，下一步；

（6）放大参数：αk=βαk，返回步骤（4）；

（7）缩小参数：αk=αk/β，u（k）=u（k）+sk， k=k+1，返回步骤（2）；

Levenberg-Marquardt算法流程图如图2所示：

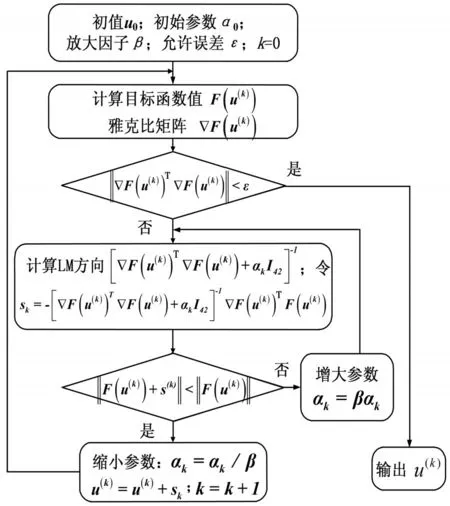
图2　Levenberg-Marquardt算法流程图

5　仿真实验

5.1设定初始参数

给定6-UPS并联机构的设计参数如下：

表1　6-UPS并联机构初始设计参数

表1中，Ru、Rd分别表示动平台、静平台铰链中心所在分布圆的半径，φu、φd分别表示动平台、静平台两个相邻铰链在分布圆上的夹角的一半，h、H分别表示动平台旋转中心与动平台、静平台铰链中心所在平面的初始距离。通过上述6个名义上的结构参数可以计算出6-UPS并联机构名义上的42个运动学参数。实际加工装配后的6-UPS并联机构必然存在误差，假定其真实误差如表2所示。但实际上，真实误差难以直接测量，需要通过实际测量的动平台的姿态进行求解，不断使42个参数逼近真实值。为使辨识的参数具有良好的鲁棒特性，本次仿真实验在6-UPS并联机构的工作空间内均匀的选取20组测量的位姿（通过正运动学仿真生成）作为动平台的实际位姿。

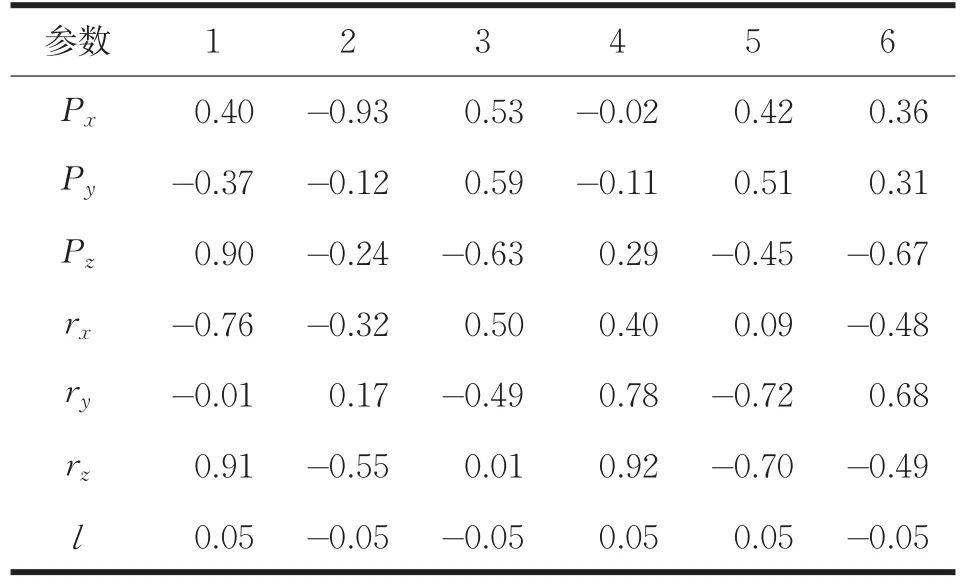
表2　假定6-UPS并联机构的运动学参数误差（mm）

5.2参数辨识结果

将5.1小节所述的平台真实位姿数据代入6-UPS并联机构的运动学辨识模型中，通过Levenberg-Marquardt算法对辨识模型进行求解，我们可以得到其参数辨识效果。其杆长变化量残差函数的变化曲线分别如图3所示。由图3可知，该算法可以迅速收敛，在迭代10次之后残差即可小于10-9mm。

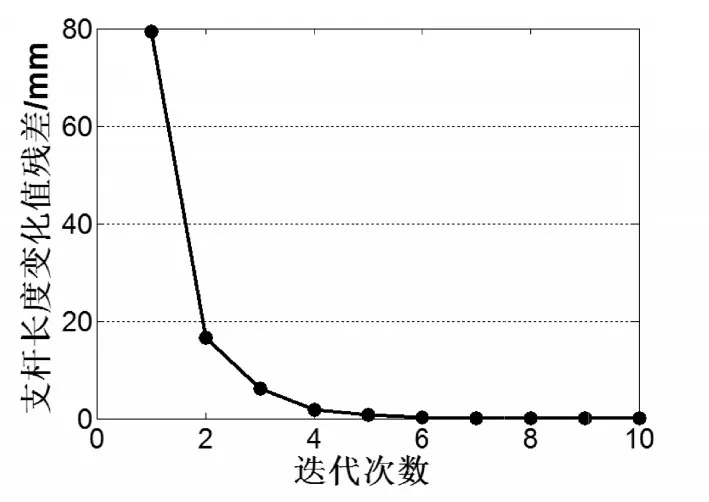
图3　杆长变化量残差变化曲线图

图4所示为参数辨识前6-UPS并联机构的运动学参数误差，量级在1mm以内。图5则表示在假设测量设备和支杆长度传感器均无误差的情况下，参数辨识后6-UPS并联机构的运动学参数误差。由图5可知，根据本文所构建的6-UPS并联机构的运动学参数辨识方法基本可以使各个参数的辨识误差接近为零（10-10mm），运动学参数辨识结果基本与实际值相同。但是实际测量设备不可能没有误差，假设测量设备的误差为±1μm和±1″，其参数辨识结果如图6所示。由图6可知，当存在误差时，6-UPS并联机构的运动学参数辨识精度有所下降，达到10-3mm，基本与外部测量设备的精度在同一数量级，可以通过6-UPS并联机构所要求的精度指标得知测量设备和测量方法所需的精度。

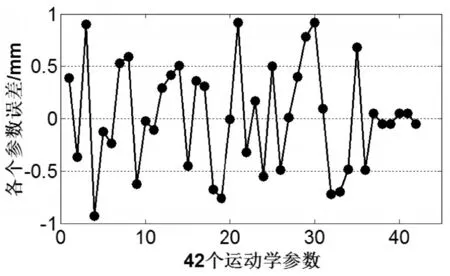
图4　辨识前的42个运动学参数误差

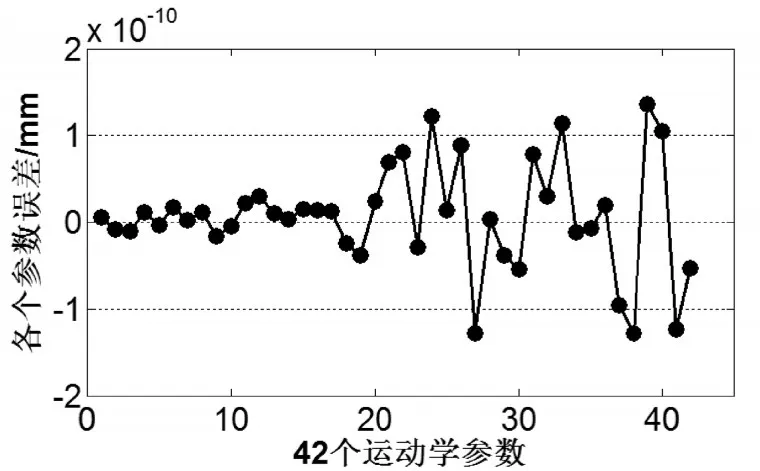
图5　测量设备无误差的情况下，辨识后的42个运动学参数误差

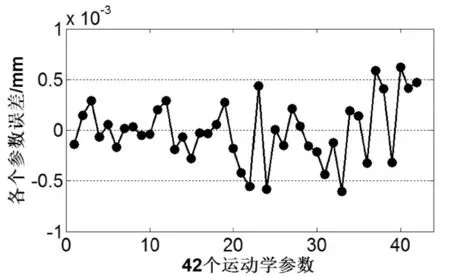
图6　测量设备存在误差的情况下，辨识后的42个运动学参数误差

6　结论

本文构建了一种基于逆运动学分析的6-UPS并联机构运动学参数辨识模型，采用Levenberg-Marquardt最小二乘法求解辨识模型，并且设计了仿真实验。结果表明，该模型可以快速收敛。在测量设备没有误差的理想状况下，参数辨识精度可以达到10-10mm，在测量设备存在±1μm和±1″的测量误差时，其参数辨识精度也可以达到10-3mm，可以满足大部分应用场合下的6-UPS的精度要求。另外，在设备有测量误差的状况下，其参数识别误差基本与测量设备在同一数量级上，据此可以为测量方法和测量设备的选择提供一定依据。

参考文献

［1］陈文家.典型并联机构的演化关系及其分类研究［J］.机械设计，2004，21（5）：1-3.

［2］张宇深，张立中，孟立新，等.六自由度摇摆台检测方案设计［J］.长春理工大学学报：自然科学版，2015，38（3）：55-59.

［3］裴葆青，陈五一，王田苗.6-UPS并联机构铰链间隙误差的标定与精度分析［J］.机械设计与研究，2006，22 （4）：35-38.

［4］李树祥.6_THRT并联机器人的标定研究［D］.南京：南京理工大学，2004.

［5］汪劲松，黄田.并联机床——机床行业面临的机遇与挑战［J］.中国机械工程，1999，10（10）：1103-1107.

［6］耿争言.Stewart平台位姿误差与标定研究［D］.西安：西安电子科技大学，2014.

［7］Takeda Y，Shen G，Funabashi H. A DBB-based kinematic calibration method for in-parallel actuated mechanisms using a fourier series［J］.Journal of Mechanical Design，2004，126（5）：856-865.

［8］罗马诺夫.误差理论与最小二乘法［M］.北京：高等教育出版社，1995：52-106.

A Method of Kinematic Parameter Identification for 6-UPS Parallel Robot Using the Inverse Kinematics Algorithm

ZHAO Haibo，LI Wei，WANG Yijian
（Changchun Insitute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033）

Abstract：A method of kinematic parameter identification for 6-UPS parallel robot using the inverse kinematics algorithm was proposed in order to improve the positioning accuracy of the 6-UPS parallel robot.Firstly，a model of kinematic parameter identification for 6-UPS parallel robot using the inverse kinematics algorithm was built.Then the model was solved by the least square method of Levenberg-Marquardt.Finally，a simulation experiment for this method was conducted.The result of the simulation experiment shows that the algorithm can converge rapidly.The identification precision of 10-10mm can be implement under the ideal condition that the measure instruments have no error.And the identification precision is 10-3mm under the condition that the measure instruments have the position error of 1micron and the gesture error of 1 arcsecond. The identification precision can meet the majority applicable situation of using the 6-UPS parallel robot.

Key words：6-UPS parallel robot；inverse kinematics；kinematic parameter identification；the least square method

中图分类号：TP242

文献标识码：A

文章编号：1672-9870（2016）02-0073-04

收稿日期：2015-10-30

作者简介：赵海波（1989-），男，硕士，研究实习员，E-mail：zhaohaibo07@sina.com