高岭土结构的多磁场27Al NMR 波谱和ab initio量子理论计算研究

苏绍明, 邹 珍

(中国冶金地质总局 中南地质勘查院，湖北 武汉 430081)

高岭土结构的多磁场27Al NMR 波谱和ab initio量子理论计算研究

苏绍明, 邹 珍

(中国冶金地质总局 中南地质勘查院，湖北 武汉 430081)

自上世纪80年代以来,试图使用魔角旋转固体核磁共振(MAS NMR)波谱来分辨高岭土结构两个不同27Al结晶位置的多次尝试均未获成功,所以本次研究试图通过结合量子理论计算和多场MAS NMR和MQMAS波谱再次尝试分辨出高岭土结构中的不同27Al位置。超高场如21 T所引起的高各向异性化学位移作用(CSA)可能会超过四极核作用(QI),这对于具较小Cq的27Al位置(如高岭土结构)而言尤为如此。而低场如4.68 T中,QI则是主宰的核磁共振作用,但是,由于高岭土结构中两个27Al位置的环境很相似,所以,通常27Al MAS NMR也无法分辨出这两个27Al 位置。结合完全势能线型增广平面波(FP LAPW)+局域轨道法(lo)、分子轨道(MO)的abinitio量子理论计算,从多量子魔角旋转波谱、卫星跃迁波谱中可得到高岭土结构中两个27Al位置的准确核磁共振参数如Cq、η、CSA 和δiso等。

高岭土;27Al MAS NMR;MQMAS;SATRAS;FP LAPW理论计算模型;CASTEP;分子轨道计算模型

1 概述

固体魔角旋转核磁共振 (MAS NMR)波谱能提供各向同性化学位移 (δiso)、各向异性 (CSA),偶极相互作用(DD)和四极核作用 (QI)等信息。这些核磁共振参数能对应着结构特征如键长、键角、配位类型、聚合度和原子间的替换[1-3],所以MAS NMR可以提供矿物在原子、分子尺度上的精细局域结构信息。例如,铝硅酸盐的27Al NMR参数与配位数、多面角畸变和聚合度间的相关性已经被成功建立[4]。但是,矿物中的多结构位置、原子间的替换所造成的无序性常造成NMR谱峰的叠合,从而降低波谱分辨率、无法得出准确的各种NMR参数。

由于非球形分布的核电荷,自旋数I>1/2的四极核拥有四极核动量(eQ)[5]。eQ与原子核所在位置的电场梯度(EFG)间的静电作用导致四极核作用,可用两个参数来描述这样的作用,即四极耦合常数(Cq)和非对称参数(η),这两个参数可以通过原子核所在位置的EFG张量来计算:

Cq=eVzzQ/h

(1)

(2)

式中:Vzz、Vxx、Vyy是主轴坐标系统(PAS)的EFG 分量,e是电子电荷单位;h普朗克常数除以2π;Q是核四极动量 (27Al 四极动量是14.6 fm2)。 QI作用常导致很宽的线型和很低的分辨率,对多位置叠合峰尤为如此。

高岭土结构已被详细研究[6-10],但是MAS NMR波谱一直没能分辨出其结构中两个不同的27Al结晶位置[11-14]。 本文试图使用多场NMR波谱并结合量子理论计算,来分辨出这两个不同Al结晶位置,如仍不能分辨,则将试图解释NMR波谱缺乏分辨率的原因。这些NMR实验包括MAS NMR、多量子魔角旋转(MQMAS)NMR、卫星跃迁(SATRAS)NMR,希望这些实验能够减弱二阶QI和其它引起线宽的因素,从而提高NMR波谱分辨率、有助于提取准确的Cq,η和δiso等参数[15-20]。完全势能线性增广平面波法(FP LAPW)和分子轨道模型(MO)将用于计算和预测结构的NMR参数,并能用来优化结构、归属NMR谱峰等。

1.1 理论计算

FP LAPW计算模型基于周期性晶体结构的对称和晶胞内原子分布,通过密度函数(DFT)来处理晶体内复杂多体电子体系的交换和相关作用,而晶胞内势能通过 Muffin-Tin 模型来模拟：即晶胞中势能分布可划分成两种区域,一种是围绕每个原子的球形势能区,而球间区域则是类似平面的势能面。 随后,由于晶体的周期性结构特征,使用Bloch原理和公式、选择完全和有效的基函数(平面波函数或球面函数)张成基底,并通过Kohn-Sham (KS)公式将晶体的多体问题简化成单体问题,经过自洽方法最终解出薛定谔方程,得到晶体波函数[21],从而可以计算出晶体的各种物理化学性质(如电子结构Cq和η),可通过软件WIEN2k来实施这样的计算[22-26]。

FP LAPW计算模型对晶胞内原子位置十分敏感,所以,通过调整晶体XRD结构的原子坐标直至晶体系统能量和或原子所受作用力达最低,此时晶体结构即达到平衡态,如此即可优化、精修晶体XRD结构[27-29]。NMR实验结果如QI参数可证实优化的精修结构。

CASTEP也是一种abinitio量子计算软件,可以计算和预测周期性结构的NMR参数[30-33]。

对于有着无序特征的晶体结构,可使用分子轨道(MO)模型来计算结构的物理、化学特性 。对晶体MO计算模型而言,首先选择目标原子如Al,在目标原子一定距离范围之内的原子组成分子族,设定收敛条件后,使用MO计算该分子族的波函数,从而可计算出相应的物理、化学性质[34]。同样地,可以使用多种方法来近似原子族内电子间的交换、相关作用如Hartree-Fock (HF)和密度函数[35]。

1.2 高岭土晶体结构

通过XRD、中子散射确定和精修了高岭土结构,并且最低能量模型也给出了结构中H原子的位置[36-37]。高岭土晶体结构空间群是C1,晶胞参数分别为a=5.153 5(3)Å,b=8.941 9(5)Å,c=7.390 6(4)Å,α=91.926(6)°,β=105.046(2)°,γ=89.797(2)°,晶胞体积V=328.70(5)Å3。高岭土具有序的中性1∶1 片层结构,片层由Al(O,OH)6八面体和SiO4四面体所组成,片层通过氢键连接在一起。

2 实验方法

2.1 试验样品

两个高岭土样品均为白色粉末状,粉晶XRD 实验证实了两个高岭土样品的纯度。室温下高岭土样品粉末XRD数据由计算机控制的ADP-2衍射仪采集,使用 CuKα 作为射线源,2的步长为0.02°、变化范围是10°～70°,每步计数时间为5 s。

2.227Al MAS NMR

所有27Al波谱均以 [Al(H2O)6]3+定标。最低场27Al MAS NMR 实验使用4.68 T、7 mm探头的Tegmac-200 谱仪,Si3N4转子、转速为8 kHz,激发脉冲宽度为 1 μs (18°)、扫描次数为 8、d1时间为0.5 s、系统死时间是 8 μs、1H去偶功率为 50 kHz。最高磁场NMR实验使用21.06 T的Bruker Avance II 900 NMR谱仪,样品转速15 kHz。在21.06 T谱仪上使用标准3QMAS脉冲序列来采集MQMAS波谱,这样的脉冲序列由两个硬脉冲及其后的z-filter脉冲所组成,3Q激发脉冲宽度是4.5 μs、3Q转换1Q的脉冲宽度1.5 μs、中心跃迁选择脉冲宽度是12.5 μs。21.06 T场1H去偶功率为100 kHz。

在7.1 T、9.4 T 和14.04 T场的Varian INOVA谱仪上运行了1H-去偶27Al MAS NMR实验,使用Si3N4转子、12 kHz转速、1 kW的去偶功率。在Varian INOVA-300谱仪上使用z-filter脉冲序列也采集了3QMAS波谱[38-43]。3Q激发和3Q-1Q转换脉冲宽度分别是4.0和1.0s,B1场强是60 kHz,90°选择脉冲宽度是20s、d1为 0.5 s。共采集128次t1增量、480 次扫描。

2.3 波谱拟合程序

DMFIT用于拟合 21T场的MAS NMR波谱和MQMAS切面波谱。δiso、Cq和η参数由手动输入直到拟合波谱与实验波谱相吻合。

2.4 FP LAPW计算

高岭土结构的晶胞参数、晶胞内原子坐标、空间群是FP LAPW WIEN2k计算的输入参数。计算使用cutoff值6.5、200 k点,在没有电荷泄露的前提下能高效运行FP LAPW计算的Al、O、Si、H原子球半径Rmt分别是1.8、1.6、1.4和 0.7 a.u.,原子球内波函数包含了高达l=12的角动量组分。采用了并行式超算模式,FP LAPW计算自洽收敛条件为 0.0001 Ry,且为非自旋极化计算模式。

2.5 CASTEP计算

使用Bish(1993)的高岭土结构,基于密度函数理论,在Materials Studio 4.3环境下使用CASTEP NMR模块计算NMR参数,并使用超软膺势、平面波基函数(cut-off值500 eV)、PBE泛函近似电子间的交换—相关作用,计算的化学屏蔽值为绝对值。

3 结果

粉晶XRD揭示高岭土样品中只有微量杂质相(<0.2 wt %),这些杂质不会干扰样品的NMR波谱。

在最低场4.68 T中,高岭土中心跃迁(CT)的27Al MAS NMR 实验波谱为半高宽约75×10-6、重心(CG)约-12.5×10-6、高场位置有肩部的非对称谱峰线型(图1-a)。在7.1 T中,CT 线型(CG 约-4.0×10-6)半高宽减小到30×10-6,但仍保持一些非对称特征,仍有高场方向的肩部 (图1-b)。11.7 T场CT线型的CG已至0.5×10-6,且线型更加平滑。14.04 T场时,CT线型(CG约4.8×10-6)就变成没有特征的Gaussian线型(图1-c)。21.06 T时,CT谱峰为很窄(半高宽5×10-6)的Gaussian线型,且CG也移至6.2×10-6(图1-d)。

图1 高岭土多场27Al MAS NMR波谱Fig.1 27Al MAS NMR spectra of kaolinite(a).4.68 T(CG=-12.5×10-6);(b).7.10 T (CG=-4.0×10-6);(c).14.04 T(CG=4.8×10-6);(d).21.06 T(CG=6.2×10-6)。

图2 高岭土27Al 卫星跃迁MAS NMR实验波谱Fig.2 27Al SATRAS spectra acquired by MAS NMR(a).21T场、15 kHz 转速;(b).11.7T场、12 kHz转速。 插图为(*±1/2～±3/2、**±3/2～±5/2)的旋转边带放大图。

11.7 T场中(图2)使用DMFIT拟合的高岭土1H去偶27Al MQMAS NMR结果列入表1,其中27Al(1)位置的δiso、Cq分别是(7.55±0.5)×10-6、3.6 MHz;27Al(2)位置则为9.0×10-6、(4.0±0.1)MHz。27Al(1)位置的η是0.57,但27Al(2)位置的η因不同拟合而给出分别为0.42和1.00不同的结果。而21 T场MQMAS波谱切面拟合的Cq和η平均值分别约1.7 MHz和0.6,这样的拟合结果与同场 MAS波谱的拟合结果相差较大。

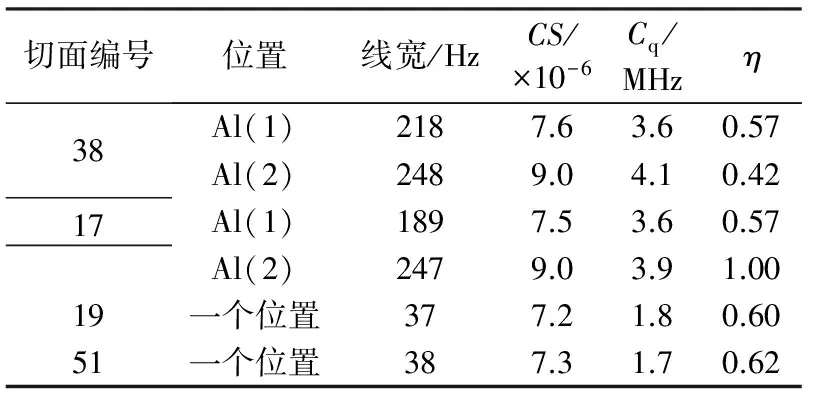
表1 11.7 T场高岭土1H去偶27Al MQMAS 波谱切面使用DMFIT拟合结果

4.68、7.1、9.4、11.04和 21 T场卫星跃迁的MAS波谱每条旋转边带可分辨出一对谱峰(图 2-a,图2-b),但7.1 T 和 21 T 场的27Al MQMAS (3Q)NMR 仍没能分辨出不同Al位置 (图3)。

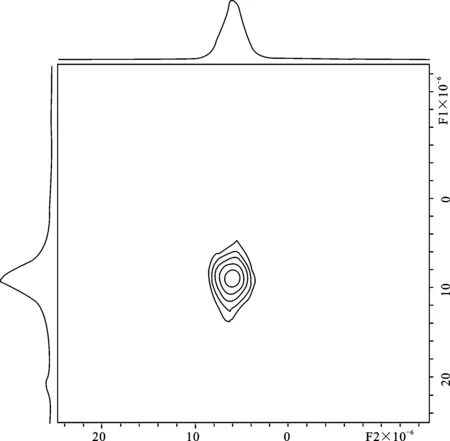
图3 21T高岭土样品1H去偶 27Al 3QMAS NMR波谱(转速15 kHz)Fig.3 1H-decoupled 27Al 3QMAS NMR spectrum at 21T with spinning speed of 15 kHz

使用WIEN2k 的FP LAPW 计算给出27Al(1)、27Al(2)位置Cq和η分别为-3.15 MHz、0.55和2.14 MHz、0.98(表2)。高岭土中两种Al位置的各向同性化学位移(δiso)、各向异性化学位移(δσ)及其对称参数(ησ)的CASTEP计算结果也列入表2。

表2 高岭土中两个Al位置使用CASTEP计算的化学位移(δiso)、各向异性化学位移参数(δσ)和对称参数(ησ),以及FP LAPW的QI参数计算值(Cq、ηQ)

4 结论

虽然XRD和中子散射识别出高岭土中两个不同Al结晶位置,但27Al NMR波谱仍没能令人信服地分辨出这两个位置[44-45]。

FP LAPW 和CASTEP 计算使用Bloch定理来考虑和处理晶体周期性结构特征和边界,使用DFT来近似体系内电子间复杂的相互作用,并通过Kohn-Sham公式将多体问题转化为单体问题,这样,FP LAPW 和 CASTEP 模型能给出具周期性结构的固体最准确的EFG、NMR等物理化学特性的理论计算结果[46]。

高岭土的27Al 每条旋转边带的两个峰(图2-a和图2-b)可能源自内、外卫星跃迁,即±5/2↔±3/2 和±3/2↔±1/2,也可能来自高岭土结构中的两个不同Al位置。由于高岭土中两个Al位置的原子数之比为1∶1,且理论计算的Cq和η结果也十分相似,所以如果每条边带中的两个谱峰源自这两个不同Al位置,那么这两个峰的宽度、强度应该类似,但是每条边带中谱峰对宽度、强度的巨大差别排除了这种可能性,所以作者支持Rocha & Pedrosa de Jesus(1994)的分析,每条边带的谱峰对应该源自卫星跃迁,而非由不同Al位置所致。对I=5/2四极核而言,外部(±5/2↔±3/2)和内部(±3/2↔±1/2)卫星跃迁的宽度和四极化学位移分别为中心跃迁的1/3和1/9[47],这就解释了每条边带的谱峰对的宽度、强度、位置对比。

如果引起线宽的因素如CSA、DD和QI 被MAS完全去除而仅留下δiso,那么这两个Al位置就可能被NMR波谱分辨出来。MQMAS NMR实验就是通过操纵多量子相互干涉、多量子转移途径,来试图去除二阶QI,并抑制 CSA和 DD 作用,从而在F1维上只留下δiso信息,F2维度仍是通常的 MAS NMR波谱。但是,高岭土中很强的同核和异核DD 作用在MQMAS实验过程中将被乘以量子干涉阶数[48],从而会降低27Al MQMAS 波谱的分辨率。高岭土中两个Al位置δiso的相似性、高场中极强的 CSA作用也会降低MQMAS波谱的分辨率。所以,高岭土的27Al MQMAS 波谱均未能分辨出不同的Al位置(图3)。

Bish (1993)指出,高岭土中可能存在H 原子站位的无序性,如此,类似于zunyite 的F/OH无序性,这也将是造成27Al MAS NMR CT谱峰叠合,引起NMR谱宽和缺乏典型QI线型[49]。

总之,由于高岭土中两个Al位置的相似性,很强的剩余CSA和DD作用,以及可能的 H 无序性,二阶QI线型特征被覆盖,导致高场中波谱无特征的Gaussian线型,从而造成需要使用很大的线宽因子(LB)来拟合27Al CT 波谱线型,这就导致了拟合过程对η和Cq变化的敏感度降低。所以,高岭土二阶CT MAS波谱和MQMAS切面波谱的拟合Cq和η值之间,以及与理论计算值存在着不一致性(表1、表2)。

然而,根据下列关系式,多场27Al MAS NMR能够为提取较为准确的NMR参数提供限制条件[50-51]：

(3)

(4)

(5)

(6)

因此,通过测量不同场中27Al MAS NMR谱峰中心 (δmcg),然后对场强因子Cm/VL2投点,使用公式(5)就能够获得参数SOQE和δiso。由于高岭土结构中两个Al位置的相似性,使用4.68、7.1、9.4、11.7、14.04和21.06 T场中CT平均δ1/2cg值与C1/2/VL2投点(图4),投点图的最小二乘法分别给出斜率和截距值-8.84和6.25,最小二乘法的相关系数高达0.998(图4)。由于斜率和截距分别对应着-SOQE2和δiso值(公式(5)),所以这两个Al位置的平均Cq值2.89 MHz,与FC LAPW理论计算值2.65 MHz十分吻合(表2),而截距6.25×10-6(δiso)也与实验化学位移和理论计算结果很接近(表1、表2),并与21 T的CT谱峰CG值几乎完全一致。这进一步证实在超高场中,高岭土QI作用降至次要地位、四极化学位移对各向同性化学位移的移动几乎可以忽略。

图4 4.68、7.1、9.4、14.04和21.06场CT NMR波谱的CG (10-6)与C1/2/VL2投点图Fig.4 Centers of gravity (CG in ×10-6)for the NMR central transitions at 4.68,7.1,9.4,14.04 and 21.06 T magnetic fields plotted against C1/2/VL2

SATRAS旋转边带总体外形(图2)也可为提取NMR参数提供进一步的限制,从而得出更为准确的结果,这是因为卫星跃迁主要受QI影响,Cq仅与SATRAS边带覆盖范围同步变化,因此可以通过SATRAS 所有边带的覆盖频率范围来估算Cq(≈ 3Cq/2I)。这种估算方法对较小Cq如高岭土中Al位置更为重要,因为较小Cq往往不能给出可供拟合的典型QI线型。 通过类比已经准确测定27AlCq的Al-F矿物如cryolithionite、cryolite的SATRAS边带所覆盖的频率范围,高岭土中27AlCq被限制在2.83～3.30 MHz间;另一方面,所有边带总体外形对η很敏感,据此高岭土中27Alη被限制在 0.7～0.9间,均与理论计算十分吻合。

因此,虽然NMR波谱没能直接分辨出高岭土中两个不同的Al晶格位置,但通过理论计算和多种NMR实验方法,高岭土中 Al 位置的NMR参数被准确测算,这种方法可应用推广至其他固体精细局域结构的研究之中。值得一提的是这项研究表明,对固体、尤其是矿物NMR而言,并非场强越高,精度和分辨率也随之越高,必须在分析固体中各种NMR作用如QI、CSA,根据这些作用对场强的响应特性,选取最优场强以获得最高分辨率和精度的NMR波谱。

[1] Smith M.E..Application of27Al NMR techniques to structure determination in solids [J].Appl.Magn.Reson.,1993,4,1-64.

[2] Ashenhurst J.,Gang Wu,G.,Wang S..Syntheses,Structures,Solution,and Solid-State27Al NMR Studies of Blue Luminescent Mononuclear Aluminum Complexes:Al(7-azain)2(7-azain-H)(CH3),Al(7-azain)3(7-azain-H),and Al(7-azain)(7-azain-H)(OCH(CF3)2)2(7-azain-H = 7-azaindole) [J].J.Am.Chem.Soc.,2000,122:2541-2547,

[3] Liu Y.,Tossell J.,Nekvasil H..A theoretical study on structural factors correlated with23Na NMR parameters [J].Amer.Mineral.,2004,89:1314-1322.

[4] Kirkpatrick R.J.,Phillips B.L..27Al NMR spectroscopy of minerals and related materials [J].Appl.Magn.Reson.,1993,4:213-236.

[5] Slichter C.P..Principles of Magnetic Resonance [M].Belin:Springer-Verlag,1992.

[6] Rocha J.,Klinowski J..The rehydration of metakaolinite to kaolinite [J]. J.Chem.Soc.Chem.Commun.,1991,3:582-584.

[7] MacKenzie K.J.D.,Meinhold R.H.,White G.V.,Sheppard C.M.,Sherriff B.L..Carbothermal formation of β-sialon from kaolinite and halloysite studied by29Si and27Al solid state NMR [J].J.Mater.Sci,1994,29:2611-2619.

[8] Rocha J..Single and triple quantum27Al MAS NMR study of the thermal transformation of kaolinite [J].J.Phys.Chem.B.,1999,103:9801-9804.

[9] Ashbrook S.E.,McManus J.,Mackenzie K.J.D.,Wimperis,S..Multiple-quantum and cross-polarized27Al MAS NMR of mechanically treated mixtures of kaolinite and gibbsite [J].J.Phys.Chem,2000,104:6408-6414.

[10] Massiot D.S.,Dion P.,Alcover J.F.,Bergaya F..27Al and29Si MAS NMR study of kaolinite thermal decomposition by controlled rate thermal analysis [J].J.Amer.Ceramic Soc.,1995,78:2940-2944.

[11] Meinhold R.H.,Mackenzie K.J.D.,Brown I.W.M..Thermal reactions of kaolinite studied by solid state 27-Al and 29-Si NMR [J]. J.Mater.Sci,1985,4:163-166.

[12] Watanabe T.,Shimizu H.,Nagasawa K.,Masuda A.,Saito H..29Si-and27Al-MAS/NMR study of the thermal transformations of kaolinite [J].Clay Minerals,1987,22:37-48.

[13] Sanz J.,Madani A.,Serratosa J.M.,Moya J.S.,Aza S..Aluminum-27 and Silicon-29 Magic-Angle Spinning Nuclear Magnetic Resonance study of the kaolinite-Mullite transformation [J].J.Amer.Ceramic Soc.,1988,71:C418-C421.

[14] Lambert J.F.,Millman W.S.,Fripiat J.J..Revisiting kaolinite dehydroxylation:A29Si and27Al MAS NMR study [J].J.Am.Chem.Soc.,1989,111:3517-3522.

[15] Wu Y.,Chmelka,B.F.,Pines A.,Davis M.E.,Grobet P.J.,Jacobs P.A..High-resolution27Al NMR spectroscopy of the aluminophosphate molecular sieve VPI-5 [J].Nature.,1990a,346:550-552.

[16] Wu Y.,Sun B.Q.,Pines A.,Samoson A.,Lippmaa,E..NMR experiments with a new double rotor [J].J.Magn.Reson.,1990b,4:203-211.

[17] Müeller K.T.,Sun B.Q.,Chingas C.G.,Zwanziger J.W.,Terao T.,Pines A..Dynamic-angle spinning of quadrupolar nuclei [J].J.Magn.Reson.,1990,84:470-487.

[18] Müeller K.T.,Wooten E.W.,Pines A..Pure-absorption-phase dynamic-angle spinning [J].J.Magn.Reson.,1991,92:620-627.

[19] Xu Z.,Sherriff B.L..27Al double-rotation NMR study of Al2SiO5polymorph minerals [J].Appl.Magn.Reson.,1993,4:203-211.

[20] Xu Z.,Sherriff B.L..23Na27Al9Be29Si solid state NMR study of tugtupite [J].Can.Mineral,1994,32:935-943.

[21] Kohn W.,Sham L.J..Self-consistent equation including exchange and correlation effects [J].Phys.Rev.,1965,140(4A):1133-1138.

[22] Blaha P.,Schwarz K.,Herzig P..First-principles calculation of the electric filed gradient of Li3N [J].Phys.Rev.Lett.,1985,54:1192-1195.

[23] Blaha P.,Schwarz K.,Dederichs P.H..First-principles calculation of the electric-field gradient in hcp metals [J].Phys.Rev.,1988,B37:2792-2796.

[24] Blaha P.,Schwarz K.,Sorantin P..Full potential linearized augmented plane wave programs for crystalline systems [J].Comp.Phys.Comm.,1990,59:39-415.

[25] Blaha P.,Singh D.J.,Sorantin P.I.,Schwarz K..Electric-field-gradient calculations for systems with large extended-core-state contributions [J].Phys.Rev.,1992,B46:1321-1325.

[26] Blaha P.,Schwarz K.,Madsen G.K.,Kvasnicka D.,Luitz J..WIEN2k,an augmented plane wave+local orbitals program for calculating crystal properties[M].Wien:Karlheinz Schwarz,Techn.Universität,2001.

[27] Bryant P.L.,Harwell C.R.,Wu K.,Fronczek F.R..Single-Crystal27Al NMR of Andalusite and Calculated Electric Field Gradients:the First Complete NMR Assignment for a 5-Coordinate Aluminum Site [J].J.Phys.Chem.,1999,103:5246-5252.

[28] Zhou B.,Giavani T.,Bildsoe H.,Skibsted J.,Jakobsen H..Structural refinement of CsNO3(II) by coupling of14N MAS NMR experiments with WIEN2k DFT calculations [J].Chem.Phys.Lett.,2005,402:133-137.

[29] Zhou B.,Sherriff B.,Hartman J.S.,Wu W..27Al and23Na NMR spectroscopy and Structural modeling of aluminofluoride minerals [J].Am.Mineral,2007,92:34-43.

[30] Profeta M.,Mauri F.,Pickard C.J..Accurate First Principles Prediction of17O NMR Parameters in SiO2:Assignment of the Zeolite Ferrierite Spectrum [J].J.Am.Chem.Soc.,2003,125:541.

[31] Clark S.J.,Segall M.D.,Pickard C.J.,Hasnip P.J.,Probert M.J.,Refson K.,Payne M.C..First principles methods using CASTEP [J].Zeitschrift fuer Kristallographie,2005,220:567-570.

[32] Pickard C.J.,Mauri F..All-electron magnetic response with pseudopotentials:NMR chemical shifts [J].Phys.Rev.,2001,245(B63):101.

[33] Yates J.R.,Pickard C.J.,Mauri F..Calculation of NMR Chemical Shifts for extended systems using Ultrasoft Pseudopotentials [J].Phys.Rev.,2007,24(B76):401.

[34] Foresman J.B.,Frisch A..Exploring chemistry with electronic structure methods,2ndEdition [M].Pittsburgh:Gaussian,Inc.,1996.

[35] Richards W.G.,Horsley J.A..AB Initio Molecular Orbital Calculations for Chemists [M].Oxford:Clarendon Press,1970.

[36] Collins D.R.,Catlow C.R..Energy-minimized hydrogen-atom positions of kaolinte [J].Acta Cryst.,1991,B47:678-682.

[37] Bish D.L..Rietvveld refinement of the kaolinite structure at 1.5 K [J].Clays and Clay Minerals,1993,41:738-744.

[38] Wu G.,Rovnyak D.,Sun B.,Griffin G..High-resolution multiple quantum MAS NMR spectroscopy of half-integer quadrupolar nuclei [J].Chem.Phys.Lett.,1995,249:210-217.

[39] Wu G.,Rovnyak,Griffin G..Quantitative multiple-quantum magic-angle-spinning NMR spectroscopy of quadrupolar nuclei in solids [J].J.Am.Soc.,1996,118:9326-9332.

[40] Wu G.,Rovnyak D.,Huang P.C.,Griffin G..High-resolution oxygen-17 spectroscopy multiple-quantum magic-angle-spinning [J].Chem.Phys.Lett.,1997,277:79-83.

[41] Amoureux J.P.,Fernandez C.,Steuernagel S..Z Filtering in MQMAS NMR [J].J.Magn.Reson.,1996,A123:116-118.

[42] Amoureux J.P,Pruski M.,Lang D.P.,Fernandez C..The effect of RF power and spinning speed on MQMAS [J].J.Magn.Reson.,1998,131:170-175.

[43] Amoureux J.P,Huguenard C.,Engelke F.,Taulelle F..:Unified representation of MQMAS and STMAS NMR of half-integer quadrupolar nuclei [J].Chem.Phys.Lett.,2002,356:497-504.

[44] Rocha J.,Pedrosa de Jesus J.D..27Al satellite transition MAS-NMR spectroscopy of kaolinite [J].Clay Minerals,1994,29:287-291.

[45] Newman R.H.,Childs C.W.,Churchman G.J..Aluminium coordination and structural disorder in halloysite and kaolinite by27Al NMR spectroscopy [J].Clay Minerals,1994,29:305-312.

[46] Zhou B.,Sherriff B.L..Quantum calculations of the electronic structure and NMR quadrupolar interaction parameters for tugtupite [J]. Am.Mineral,2004,89:377-381.

[47] Jäger C..How to get more from27Al MAS NMR by high-speed satellite-transition spectroscopy [J].J.Magn.Reson.,1992,99:353-362.

[48] Lacassagne V.,Florian P.,Montouillout V.,Gervais C.,Babonneau F.,Massiot D..Resolution enhancement in solid-state MQ-MAS experiments achieved by composite decoupling [J].Magn.Reson.Chem.,1998,36:956-959.

[49] Zhou B.,Sherriff B.L.,Taulelle F.,Wu G..Nuclear Magnetic Resonance Study of Al:Si and F:OH order in Zunyite [J].Can.Mineral,2003,41:891-903.

[50] Samoson A..Satellite transition high-resolution NMR of quadrupolar nuclei in powders [J].Chem.Phys.Lett.,1985,119:29-32.

[51] Skibsted J.,Nielsen N.,Bildsøe H.,Jakobsen H.,Satellite transitions in MAS spectra of quadrupolar nuclei [J].J.Magn.Reson.,1991,95:117-132.

(责任编辑：陈文宝)

Calculation study of27Al NMR Spectrum in Muti-magietic Field with KaoliniteStructure and ab initio Quantum Theory

SU Shaoming, ZOU zhen

(CentralSouthInstituteofGeologicalExploration,ChinaGeneralBureauofMetallurgyGeology,Wuhan,Hubei430081)

Many unsuccessful attempts have been made to resolve the two different Al sites in kaolinite by magic angle spinning nuclear magnetic resonance (MAS NMR) spectroscopy since the early 1980’s. This study attempted to resolve these sites and explain the reasons for the lack of separation by combining NMR spectroscopy at various fields with ab initio quantum modeling. Ata high field such as 21.06 T, large chemical shift anisotropy (CSA) and dipolar effects (DD) can overwhelm the quadrupolar (QI) effects for sites with relatively smallCqvalues such as the two Al sites in kaolinite, so the spectra display featureless line-shapes lacking the typical QI singularities and shoulders. At lower fields such as 4.68 T, the QI effects become dominant but due to the similarity of the two Al environments in kaolinite, the27Al MAS NMR peaks could not be separated either. Theoretical ab initio quantum modeling using Full Potential Linearized Augmented Plane Wave (FP LAPW) and Molecular Orbital (MO) allowed experimental27Al MAS NMR, multiple quantum (MQ) MAS and satellite transition (SATRAS) spectra to be interpreted.Cq,η, CSA andδisofor the two Al sites were obtained with high accuracy by simulating these spectra, while constraining the QI parameters.

Kaolinite;27Al MASNMR; MQMAS; SATRAS; Calculation model of FP LAPW; CASTEP; Calculation model of molecular orbital

2015-05-07;改回日期:2016-03-21

本文得到湖北省国土资源厅(编号为ETZ2015A05)科研项目的资助。

苏绍明(1965-),男,高级工程师,矿产普查与勘探专业,从事地质找矿工作。E-mail:78737567@qq.com

O641

A

1671-1211(2016)02-0211-06

10.16536/j.cnki.issn.1671-1211.2016.02.017

数字出版网址:http://www.cnki.net/kcms/detail/42.1736.X.20160303.1642.038.html 数字出版日期:2016-03-03 16:42