公交乘客满意度相关因素的影响程度分析

欧阳剑，胡郁葱，李橘云，李健行

1)广州市交通规划研究院技术咨询所，广东广州 510030； 2)华南理工大学土木与交通学院，广东广州 510640



公交乘客满意度相关因素的影响程度分析

欧阳剑1，胡郁葱2，李橘云1，李健行1

1)广州市交通规划研究院技术咨询所，广东广州 510030； 2)华南理工大学土木与交通学院，广东广州 510640

摘要：通过大量乘客满意度问卷调查，利用朴素贝叶斯分类法，建立候车时间、步行时间和乘车环境满意度等9个属性与乘客总体满意度之间的满意度模型，该模型预测精度达79.9%．结果表明，候车时间与乘客总体满意度之间呈非线性关系，当乘客候车时间<5 min的比例<33.8%时，候车时间<5 min的比例每增加1%，乘客总体满意度增加0.07%；当乘客候车时间<5 min的比例>33.8%时，候车时间<5min的比例每增加1%，乘客总体满意度增加0.04%．

关键词：交通运输系统工程；常规公交；乘客满意度；候车时间；朴素贝叶斯；非线性关系

公共交通是城市公共基础设施之一，是城市政治、经济及文化生活不可或缺的纽带．对常规公交而言，服务水平评价有利于及时发现公交系统中的薄弱环节，有利于改善城市公交客运服务水平，甚至可为提高公共交通综合服务水平提供依据．目前，对公交服务水平的研究主要利用客观指标进行综合评价．武荣桢等[1]运用层次分析法从线网布局和客运能力水平方面对咸阳市公共交通进行评价；徐兵[2]从平均站距和满载率等方面建立公交服务水平评价体系，采用灰色关联分析法对沈阳市公共交通进行分析；孙慧娟[3]从方便、安全及舒适等方面，运用粗糙集决策分析法对济南市快速公交系统(bus rapid transit，BRT)进行评价．由于利用客观性能指标得出的服务水平评价，容易造成设计人员的主观臆想，导致评价与实际公交乘客的感知存在差距，因此，需要注重乘客感觉的主观因素分析．该方面研究在国内较少，主要因乘客满意度调查操作比较困难，且花费的人力和财力较大．Gabral等[4]研究了乘客对于公交服务的态度，表明公交感知服务质量对乘客使用公交出行相关性很大；Hiroyuki等[5]通过对洛杉矶公交停靠站乘客满意度调查，发现乘客满意度很大程度受车头时距、步行时间及车辆运行可靠性影响，而与站点物理设施关系不大；刘建荣等[6-7]利用联合分析法对乘客偏好进行研究，表明可靠性对乘客偏好影响较大，而步行环境、站台环境对乘客偏好影响较小，其后又运用结构方程模型探索了乘客满意度、乘客期望、感知质量、公交形象和乘客忠诚等之间的因果关系，其结论表明每提升1单位的感知质量，乘客满意度提高0.81单位，但该模型假设各因素之间为线性相关．目前大多研究只对公交服务水平进行综合评价，有关服务水平改善措施对公共交通总体满意度提升的定量分析研究相对较少，事实上改善措施与公交服务水平并不一定呈线性相关．

本研究基于广州市对2011—2012年新开100条公交线路的乘客满意度问卷调查[8]，针对乘客主观感受所得大量离散、有序及有限的问卷数据，利用朴素贝叶斯方法建立适用该调查结果的乘客满意度模型，并利用该模型对提升新开100条公交线路服务水平的建议措施进行效果预测，得到了候车时间与乘客满意度的非线性关系．

1朴素贝叶斯方法

1.1贝叶斯基本理论

(1)

1.2朴素贝叶斯分类技术

设一个数据样本有n个属性，以n维向量 x={x1,x2,…,xn}表示n个属性的取值；假设所有数据样本归属于m个类别，以m维向量 c={c1,c2,…,cm}表示所有类别，贝叶斯分类过程就是判断这些样本分别属于哪个类别．

朴素贝叶斯基于这样一个假设，即当给定分类变量时，属性变量之间条件独立[9]，即在给定实例的目标值情况下，观察到联合x1,x2,…,xn的概率正好是对每个单独属性的概率乘积，即要满足

(2)

因此，根据贝叶斯公式(1)及式(2)，可推断某一样本x={x1,x2,…,xn}属于各个类别cj的概率，具体过程为

朴素贝叶斯分类是找到这一样本数据x具有最大概率的类别cMAP， 即

j∈(1,2,…,m)}

(3)

(4)

(5)

其中， N为样本数据中的总样本数； sj为样本数据中属于cj类别的样本数； sji为样本数据中属于cj类别且含有xi的样本数．

2贝叶斯乘客满意度模型

2.1数据来源

2012年，广州市对新开的100条公交线路进行运营评估，这些公交线路主要是市中心区外围的短途公交线和连接中心区与郊区的接驳线．该评估主要是对这100条线路跟车满意度进行问卷调查，在高峰时段共发放问卷8 640份，回收8 184份，平均每条线路回收问卷80余份，有效率为94.7%，总体的问卷抽样率为4.2%，包含了不同年龄段及职业等的乘客，认为样本有效可靠，具有较好的代表性．

问卷主体设计包括两大部分：出行特征，包括步行到达公交站点时间(5个选项)及公交站点候车时间(5个选项)；满意度评价，包含线路走向、站点设置、发车频率、准点率、候车环境、车型、乘车环境及对总体满意度进行满意度评价，每个调查项提供满意、比较满意、一般和不满意4个选项供被调查者选择．

2.2模型建立

相关朴素贝叶斯分类技术独立性假设研究表明：朴素贝叶斯分类模型的表现和独立性假设是否满足没有必然联系[10-11]．根据乘客满意度调查问卷的构成可知，步行时间和候车时间等相当于贝叶斯模型中的状态属性 x， 乘客总体满意度相当于分类属性 c， 各属性取值如表1．根据离散属性相关性分析[12]，状态属性中候车时间与发车频率相关度最大，采用交叉验证法测试，是否删除发车频率对预测乘客总体满意度的影响不大，准确率误差平均约2%．因此，本研究案例同样认为独立性假设对本次研究影响不大．

表1　乘客满意度模型属性构成

在对“比较年新开的100条线路”问卷调查中，实际回收8 000多份问卷，在本模型中，为便于计算，对填写不完整的问卷暂时不予考虑，因此，本模型实际利用的数据样本容量为7 011份．

朴素贝叶斯分类模型通常将样本数据分为训练集与测试集．首先，基于训练集根据式(4)与式(5)得出相关参数；其次，基于测试集中的状态属性根据式(3)得出分类属性的预测值；最后，对比分析分类属性预测值与调查得到的分类属性值获取模型的准确率．

本研究运用交叉验证法划分训练集与测试集，即训练模型3次，第1次选取每条线路前1/3的样本作为测试集，后2/3的样本作为训练集(事先对每份问卷进行编号)；第2次选取每条线路中间1/3的样本作为测试集，前1/3与后1/3的样本作为训练集；第3次选取每条线路的后1/3样本作为测试集，每条线路的前2/3样本作为训练集．最后3次试验取平均，作为本模型的准确率．

依据式(4)和式(5)，以第1次训练情形为例，在计算先验概率时，训练样本总数为4 674份，分类属性乘客总体满意度为满意的样本数为914份，故乘客总体满意度为“满意”的先验概率为0.196；在计算条件概率时，假设计算在乘客总体满意度为“满意”的基础上，步行时间为“一般”，此时样本数为530份，故其条件概率为0.580，其他依此类推．基于Matlab编程测算[13]，模型试验结果如表2，模型准确率仅有63.5%，精度不高，经探究发现，预测时分类属性满意与比较满意之间容易误判，即满意的容易预测为比较满意，比较满意容易预测为满意．事实上，当交通管理人员去评估乘客总体满意度时，认为比较满意已到达较高水平，此时不区分满意与比较满意已能满足评估需要．故对满意与比较满意不进行区分，均认为其满意，此时模型分类属性变为满意、一般和不满意3个类别，重新对模型进行标定与测算，获取改进模型的预测准确率达79.9%，预测精度拥有较大幅度的提高，能较准确的预测相关改善公交服务水平措施所能提升的乘客总体满意度．

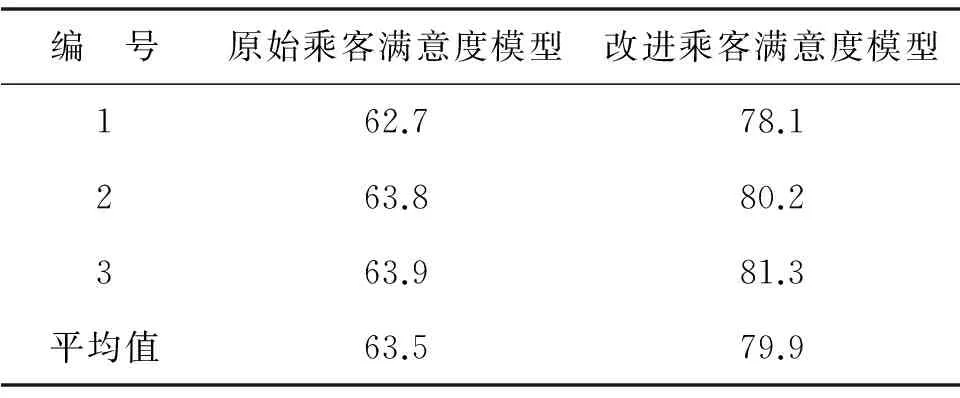
表2　试验结果(准确率)

3乘客满意度改善措施效果评价

对各属性与乘客总体满意度进行相关性分析，乘客候车时间与总体满意度的相关性最大，在问卷调查中，高峰期乘客候车时间在10 min之内的仅占60%多，同时也是各属性满意度评分最低的指标[8]，因此，选取乘客候车时间作为影响乘客总体满意度的一大重要因素．

本研究模拟实施改善候车时间措施后(如加大发车频率等)，乘客候车时间有所下降，此时在原有调查问卷的基础上，调查问卷候车时间发生如表3的改变，共模拟了6种情形，即在现状候车时间基础上，原先候车时间为6～10、11～15、16～20及>20 min中的乘客各有10%、20%、30%、50%和100%的乘客变为<5、6～10、11～15和16～20 min，以及全部乘客的候车时间均在5 min以内，见表3，其余属性不变，基于改进乘客满意度模型对乘客总体满意度进行预测．具体过程为：

第1步．获取改进乘客满意度模型参数值．通过总计的7 011份问卷来进行训练．

第2步．获取实施改善措施后再次调查可能获取的样本．首先对现有样本按候车时间的属性值进行排序，利用交叉验证法获取改善措施实施后再次调查可能得到的问卷结果，如改善情形1，将会出现10种可能的问卷结果(事实上可能存在无数多种情况，由于均是随机调查和随机排序，本研究认为采用交叉验证法能获取具有典型代表性的可能样本)，具体过程类似于训练集与测试集的划分，其他情形依此类推．

第3步．获取乘客总体满意度预测值．根据不同情形获取的样本进行预测，当可能样本出现多个时(如改善情形1—4)，取预测值的平均值为该情形的总体满意度预测值．

表3　改善措施实施后乘客可能候车时间构成

图1　乘客总体满意度与候车时间关系Fig.1　The relationship between passenger satisfactions and waiting time

候车时间不同改善水平同乘客总体满意度的关系如图1，候车时间<5 min的比例越大，乘客满意度越大，但并不成线性关系，具体为：当乘客候车时间<5 min的比例<33.8%时，候车时间<5 min的比例每增加1个百分点，乘客总体满意度增加0.07个百分点；当乘客候车时间<5 min的比例>33.8%时，候车时间<5 min的比例每增加1个百分点，乘客总体满意度增加0.04个百分点，以图1虚线为界．

结语

本研究基于朴素贝叶斯方法，建立公交乘客满意度模型，经验证模型预测精度较高，且运用候车时间的改善对提升公交服务水平做了预测，给出候车时间与总体满意度之间的关系．本研究仅呈现一种主要因素与乘客总体满意度之间的关系，且未考虑相关改善措施所需的资金投入，下一阶段拟从资金投入，多措施组合改善着手，提出改善公交满意度水平更有效、更经济的建议方案．同时，该模型对总体满意度为满意与较满意的辨别能力较差，后续研究将结合“互联网+”的盛行，从模型构建开展深入研究．

参考文献/References：

[1] 武荣桢, 翟栋栋, 郗恩崇, 等. 城市公共交通服务满意度评价模型[J]. 交通运输工程学报, 2009, 9(4): 65-70.

Wu Rongzhen, Zhai Dongdong, Xi Enchong, et al. Evaluation model of satisfaction degree for urban public transit service[J]. Journal of Traffic and Transportation Engineering, 2009, 9(4): 65-70.(in Chinese)

[2] 徐兵. 城市公交服务水平评价研究[D]. 长春: 吉林大学, 2011.

Xu Bing. Research on service level evaluation of public transportation[D]. Changchun: Jilin University, 2011.(in Chinese)

[3] 孙慧娟. 城市快速公交服务水平评价研究[D]. 成都: 西南交通大学, 2009.

Sun Huijuan. The evaluation of the service level for BRT[D]. Chengdu: Southwest Jiaotong University, 2009.(in Chinese)

[4] Beirão G, Cabral J A S. Understanding attitudes towards public transport and private car: a qualitative study[J]. Transport Policy, 2007(24): 478-489.

[5] Iseki H, Taylor B D. Style versus service? An analysis of user perceptions of transit stops and stations[J]. Journal of Public Transportation, 2010, 13(3): 39-63

[6] 刘建荣, 邓卫, 张兵. 基于联合分析的公交服务质量研究[J]. 交通运输系统工程与信息, 2011, 11(4): 97-102.

Liu Jianrong, Deng Wei, Zhang Bing. Conjoint analysis based transit service quality research[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(4): 97-102.(in Chinese)

[7] 刘建荣. 公交通行能力及服务水平研究[D]. 南京: 东南大学, 2011.

Liu Jianrong. Transit capacity and service quality analysis[D]. Nanjing: Southeast University, 2011.(in Chinese)

[8] 胡郁葱, 陈海伟, 欧阳剑，等. 2012年广州市新开公交线路客流特征及满意度评价研究报告[R]. 广州市交通委员会,2012:5-9,13-15.

Hu Yucong, Chen Haiwei, Ouyang Jian, et al. A study report of Guangzhou new bus lines passenger flow characteristics and satisfaction evaluation in 2012[R]. Guangzhou Transport Planning Board, 2012:5-9, 13-15.(in Chinese)

[9] 米切尔, 曾华军. 机器学习[M]. 北京：机械工业出版社, 2003:127.

Mitchell T, Zeng Huajun. Machine learning[M]. Beijing: Mechanical Industry Press, 2003:127.(in Chinese)

[10] Hand D J，Yu K. Idiot’s Bayes-not so stupid after all?[J]. International Statistical Review，2001(69)：388-369.

[11] 范金金, 刘鹏. 朴素贝叶斯分类器的独立性假设研究[J]. 计算机工程与应用, 2008, 44(34): 139-141.

Fan Jinjin, Liu Peng. Research on Naive Bayesian classifier’s independence assumption[J]. Computer Engineering and Applications, 2008, 44(34): 139-141.(in Chinese)

[12] 张静，王建民，何华灿. 基于属性相关性的属性约简新方法[J].计算机工程与应用，2005，41(28)：55-57.

Zhang Jing, Wang Jianmin, He Huacan. A novel feature reduct algorithm based on feature correlation[J]. Computer Engineering and Applications, 2005, 41(28):55-57.(in Chinese)

[13] 梅志红, 杨万. MATLAB程序设计基础及其应用[M]. 北京：清华大学出版社有限公司, 2005:193-200.

Mei Zhihong, Yang Wan. MATLAB programming foundation and its application[J]. Beijing: Tsinghua University Press, 2005:193-200.(in Chinese)

【中文责编：方圆；英文责编：木南】

Influence analysis of the factors related to bus passenger gross satisfaction

Ouyang Jian1, Hu Yucong2, Li Juyun1†, and Li Jianxing1

1) Technical Consultation Department, Guangzhou Transport Planning Research Institute,Guangzhou 510030, Guangdong Province, P.R.China 2) School of Civil Engineering and Transportation, South China University of Technology,Guangzhou 510640, Guangdong Province, P.R.China

Abstract：On the basis of a large number of questionnaires, a model is proposed to describe the relationship between passenger gross satisfaction (PGS) and nine properties such as passenger waiting time, walking time, travel conditions and so on by using the Naive Bayes classifier. The model achieves the prediction accuracy of 79.9%. The results show that the relationship between PGS and bus waiting time is nonlinear. If the proportion of bus waiting time, which is less than 5 min (PBWT5), increases by 1 percent, the PGS will increase by 0.07 percent when PBWT5 is less than 33.8%. However, when PBWT5 is over 33.8%, if PBWT5 increases by 1 percent, the PGS will increase by 0.04 percent.

Key words：transportation system engineering; regular public transit; passenger gross satisfaction; waiting time; Naive Bayes; non-linear relationship

基金项目：国家自然科学基金资助项目(61174188)

作者简介：欧阳剑(1988—)，男，广州市交通规划研究院助理工程师. 研究方向：数据挖掘分析. E-mail：1131551023@qq.com

中图分类号：U 491

文献标志码：A

doi：10.3724/SP.J.1249.2016.03288

【交通物流 / Transportation Logistics】

Received：2015-12-14；Accepted：2016-03-02

Foundation：National Natural Science Foundation of China (61174188)

† Corresponding author：Senior engineer Li Juyun. E-mail: 27469198@qq.com

Citation：Ouyang Jian，Hu Yucong, Li Juyun, et al. Influence analysis of the factors related to bus passenger gross satisfaction[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(3): 288-292.(in Chinese)

引文：欧阳剑，胡郁葱，李橘云，等. 公交乘客满意度相关因素的影响程度分析[J]. 深圳大学学报理工版，2016，33(3)：288-292.