需求分布未知下含数量折扣的多产品库存与定价

张文思，李金林，王建才，冉伦



需求分布未知下含数量折扣的多产品库存与定价

张文思，李金林，王建才，冉伦

（北京理工大学管理与经济学院，北京 100081）

考虑需求分布未知情况下含数量折扣的多产品库存与定价联合问题，建立混合整数非线性规划模型，假设已知信息为随机需求扰动的均值和方差，通过引入最大化最坏情况下利润的max-min准则给出期望利润的下界。在此基础上，利用拉格朗日对偶处理约束条件，根据成本折扣区间将原问题分解为若干个子问题；证明了拉格朗日松弛问题的目标函数为关于库存因子的凹函数和关于定价的拟凹函数，并给出最优定价和最优订货量的表达式，设计启发式算法对模型进行求解。最后通过数值算例对算法的鲁棒性和有效性加以说明，并分析了参数变化对最优解的影响。

需求分布未知；多产品；库存；定价；数量折扣

0 引言

报童问题是经典的单周期库存问题，考虑了随机不确定需求下寻求使得期望利润最大化的产品最优订购量问题[1]。随着顾客需求多样化的增加和市场需求不确定性的增高，越来越多的研究学者在经典报童问题基础上对运作管理相关问题展开分析。Khouja对报童问题的研究进行了全面回顾，并将对经典报童问题的扩展研究分为11个类别，其中包括存在资源约束的多产品报童问题、库存与定价联合模型、供应商提供数量折扣的报童问题以及不同需求信息情形的报童问题[2]。

当零售商销售多种产品时，其决策可能会受到多种资源约束条件的限制，如资金预算存在上限的成本约束、仓库容量有限的库存约束等，忽略资源约束条件会产生非可行解，因此零售商需决定如何分配有限的资源以最大化期望利润。含有资源约束的多产品报童问题已经取得了广泛的研究成果。Hadley和Whitin首先考虑了含有单个约束条件的多产品报童问题，并利用拉格朗日乘子、莱布尼兹法则、动态规划等方法求解[3]；此后，Lau和Lau进一步地将研究推广到了存在多个约束条件的情形[4]。Abdel-Malek和Montanari分别研究了含有一个约束条件和两个约束条件的多产品报童问题的解空间[6,7]。随着生产技术的进步和销售环境的复杂化，多产品报童模型被更多的研究者关注，越来越多的研究方法如二次规划、近似、二分算法等被用来处理含有约束条件的多产品报童问题，相关研究包括Abdel-Malek和Areeratchakul[8]、Niederhoff[9]、Zhang等[10]。

早期有关报童问题的研究往往假设价格为外生变量，即需求是不依赖于市场价格的随机变量，因而忽略了价格因素对产品需求的影响。Whitin最早建立了考虑价格影响需求的报童模型，模型通过假设需求分布依赖于单位销售价格，将销售价格由外生参数转变成为决策变量，并得到了最优订货量关于销售价格的函数表达式，相应的，最优销售价格也可以表示成最优订货量的函数[11]。随后，Lau和Lau、Polatoglu探讨了需求随机且价格弹性的报童问题订购与定价联合决策问题[12],[13]，Petruzzi和Dada在全面回顾单周期随机库存研究的基础上，完善了将销售价格视作内生变量的报童模型理论框架，并分别研究了需求关于销售价格的加法函数形式与乘法函数形式，证明了最优解及其存在条件，丰富了报童问题的研究成果[14]。上述研究均针对单产品进行展开，Murra等将研究扩展到了存在预算约束时的多产品库存与定价联合模型，且假设产品需求之间存在交叉弹性，即某一产品的需求依赖于其他产品的需求[15]。

在实际操作中，供应商普遍通过提供价格折扣促使零售商订购更多数量的产品。对零售商来说，产品订单数量越大，单位采购成本就越低。供应商提供的折扣形式多样，被广泛采用的主要是全量折扣（all-units discount）和增量折扣（incremental discount）[16]。对于存在产品数量折扣的库存问题，Pantumsinchai和Knowles 建立了存在数量折扣的单周期库存模型[17]，Khouja研究了利用多等级折扣出售剩余库存的报童问题[18]， Khouja和Mehrez进一步分析了多产品、多价格折扣的报童问题[19]。Zhang考虑了同时存在资源约束和供应商提供数量折扣的多产品报童问题，建立混合整数非线性规划并提出拉格朗日松弛算法对该问题进行求解，并通过大规模算例对算法有效性加以说明[20]。Shi和Zhang在此工作的基础上，考虑价格为决策变量，研究了需求关于销售价格的加法函数形式下的多产品报童问题[21]。

经典随机库存理论假设需求分布信息已知，即决策者在假定的需求分布条件下求解随机优化问题；而在实际中，决策者很难根据需求样本判断出其精确的分布形式，仅能通过样本信息获得需求分布的部分信息。基于此，Scarf通过给出期望利润函数的下界值，对仅知均值和方差的随机需求进行了确定性近似；这种近似保证了即使在最坏分布情况下决策者也能获得收益[22]。这种基于鲁棒优化思想的方法在随后的研究中获得了广泛的应用。Perakis和Roels对部分需求分布信息（均值、方差、对称性等）下的报童问题进行研究，利用最小化最大后悔值模型给出了最优订货量，并证明了该方法的鲁棒性[23]。Qiu等考虑了决策者为风险规避时，已知部分需求信息的库存问题[24]。Raza研究了分布未知情况下的库存与定价联合模型，给出了已知需求期望和方差时的目标函数下界值，证明了该下界关于价格和订货量为联合凹函数；指出通过这种方法可以得到最优定价和订货量的闭式解[25]。

表1 报童问题扩展研究

对部分现有成果进行归纳可以发现，目前对报童问题的扩展研究往往只针对上述提到的其中几个方面展开，见表1。本研究拟在Zhang[20]、Shi和Zhang[21]以及Raza[25]的研究基础上，利用Scarf[22]提出的信息不完全时的最大化最坏情况下的期望利润，即max-min决策准则，综合考虑需求分布信息未知情况下的多产品报童库存与定价联合问题，建立混合整数非线性规划模型，利用拉格朗日松弛得到存在数量折扣和单个约束条件下最优订货量和最优定价的表达式，并设计算法进行求解，通过数值算例对决策准则的鲁棒性进行说明，并给出参数变化对最优解的影响。本文其余部分组织如下：第1节给出符号说明及多产品库存与定价联合问题的基本描述，并给出max-min准则下的目标函数下界；在第2节利用拉格朗日松弛对模型进行求解，给出每个产品在不同折扣区间的最优定价与最优订货量的表达式，并设计启发式算法获得问题的最优解；第3节在1、2节的基础上，通过算例分析对最坏情况下的最优解的有效性和鲁棒性进行验证，并分析参数变化对最优解影响；最后结论将在第4节给出。

1 问题描述与模型假设

指标

参数

根据上述符号描述，对于存在数量折扣的多产品报童问题，我们有：

决策变量

因此，最大化期望利润的目标函数及其约束条件可写为：

(1)

s.t.(2)

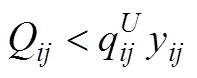
(4)

(5)

(7)

(8)

(10)

根据(9)和(10)，可将(1)中的期望利润函数改写为：

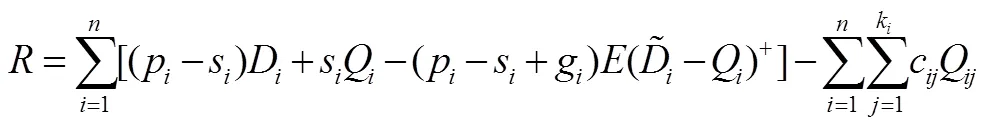
(11)

证明可参见Gallego和Moon[33]。

可以看出，(11)式给出了原问题的下界，即乘法需求模式下最坏情况下的期望收益函数：

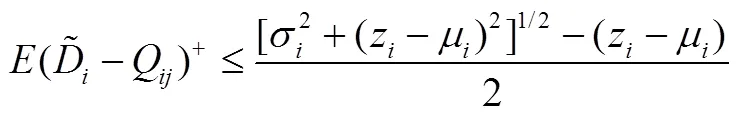
可得加法需求下，最坏情况时的期望收益函数：

由此，原问题转化为求解最坏情况下的最优期望利润，使得其满足约束条件(2)-(8)，其中乘法需求下，；加法需求下。

2 求解方法

对于上述混合整数线性规划问题，可通过将各产品各折扣区间进行组合，并采用分支定界法进行求解；然而基于原问题的复杂性，通过枚举所有组合情形会降低求解效率。下面提出基于拉格朗日松弛的启发式算法对该问题进行求解。

2.1 拉格朗日松弛

由于资源约束的存在，原问题相当于求解一个含有约束的非线性优化问题，因此可通过引入拉格朗日乘子，对约束条件(2)进行松弛，可得如下拉格朗日对偶问题：

LD:

满足约束条件(3)-(8)。

RP:

满足约束条件(3)-(8)。

，

上述松弛问题可分解为如下个子问题SPi，每个子问题对应一种产品。

SPi:(15)

s.t.(16)

(18)

(19)

(21)

SPij:(22)

s.t.(23)

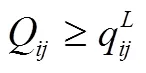
其中乘法需求模式下

，

加法需求模式下

，

相应的，加法需求模式下有：

，，

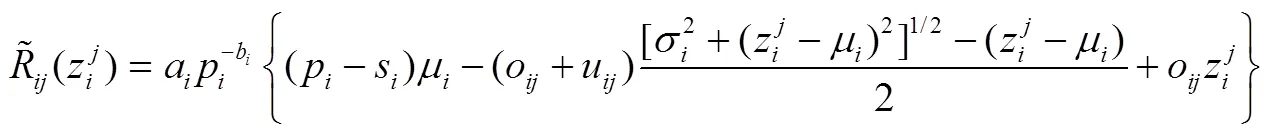
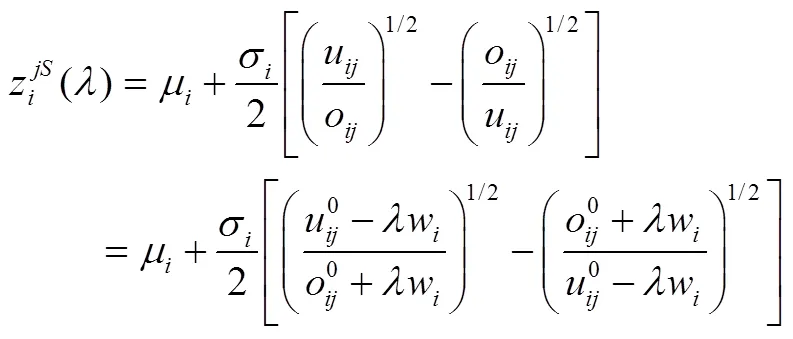
等价地，

。

同理可证得加法需求模式下仍有上述结论成立。□

，

，

。

，

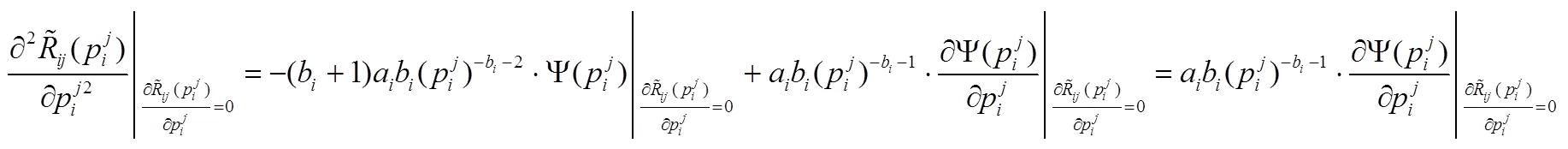
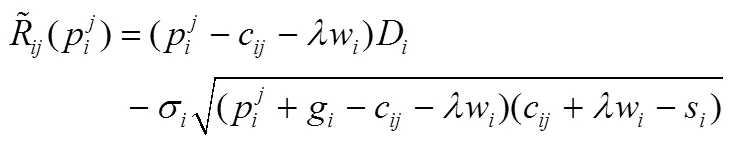
由Raza[25]，满足一阶条件的价格存在且唯一，因此对于部分信息的多产品数量折扣报童问题，max-min准则下最优定价应满足：

算法A（求解子问题SPij）

其中，乘法需求模式下

加法需求模式下

。

Step 2.确定max-min准则下的最优订货量。

其中乘法需求模式下

加法需求模式下

,

证明：

(1) 显然。

算法B（求解子问题SPi）

Step 2.利用算法A计算无约束下子问题SPij的最优鲁棒价格和订货量。

其中乘法需求模式下，

。

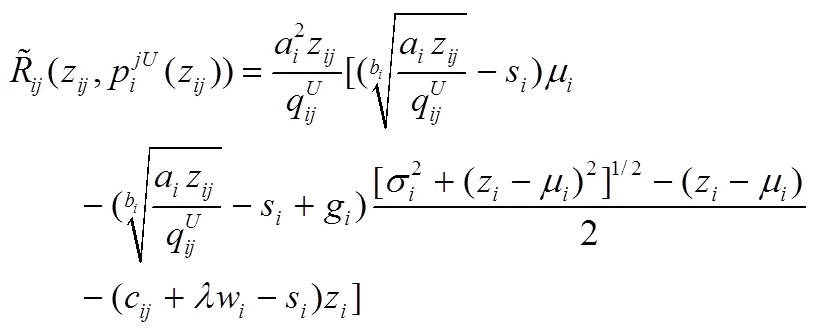
加法需求模式下，

。

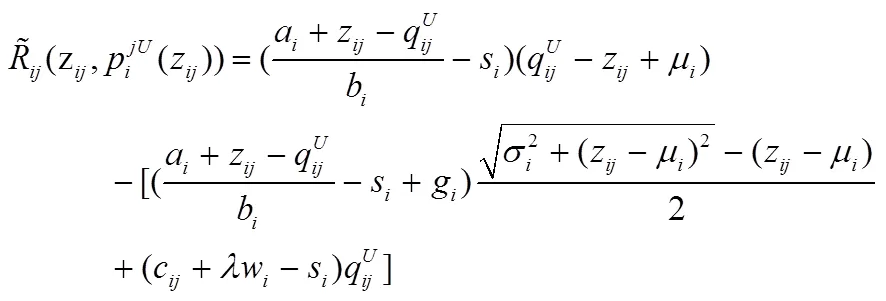
其中乘法需求模式下

，

加法需求模式下

命题2算法B得到的解是子问题SPi的最优解。

(25)

算法从最低的成本价格开始计算，当获得第一个满足最优性条件的订货量时停止迭代，下面我们说明这一算法的可行性。不失一般性，假设产品在第个折扣成本区间订货量满足最优性条件，根据(25)式，无须对的子问题SPij进行求解。

2.2 求解拉格朗日对偶问题

算法C（二分法迭代寻找最优拉格朗日乘子）

2.3 构造可行算法

即，

(27)

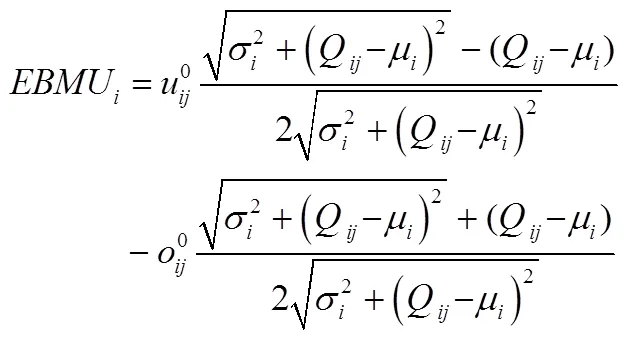
算法D（调整非可行解，改进可行解）

3 数值算例

下面通过设计数值算例说明上述方法的有效性。为更好的说明数值结果，采用Shi和Zhang[21]的数据参数并与其结果进行对比。假定某零售商需采购5种产品，资源约束条件采用成本约束，其中总成本预算上限()为125,000，产品随机需求为加法需求模式，5种产品的随机扰动因子相互独立，且服从均值为0的正态分布。每种产品有三个成本折扣区间，各产品的参数由表2给出。

为说明在部分需求信息下本文所采用max-min准则的有效性，表3对比了实际分布为正态分布时已知全部信息的情形下的最优解（参见Shi和Zhang[21]）、决策者仅知随机需求扰动项均值和方差的情形下利用Scarf[22]提出的max-min准则求得的最优解以及实际分布为正态分布而决策者利用均匀分布求解获得的最优解。从结果中可以看出，max-min方法获得的结果要优于采用均匀分布获得的结果，且与需求分布已知情形下获得的最优期望差距较小，因此可以从一定程度上说明max-min准则在已知部分需求信息情形下具有较好的鲁棒性。表3还给出了已知部分需求信息时供应商不提供数量折扣（即所有产品的采购成本固定）的最优解和最优值，通过对比可以发现，当供应商提供数量折扣时，决策者的订货量会增加，而最优定价则会降低。这说明，供应商提供数量折扣会促进零售商订购更多的产品，而成本的降低也会使零售商选择降低售价来增加产品需求，因此供应商和零售商都可以从数量折扣中获得收益。

表2 算例参数

表3 部分需求信息下求解方法有效性对比

下面分析参数变化对最优解的影响。图1分别给出了成本约束的变化在需求分布已知[21]、部分需求信息以及无数量折扣情形下对决策者最优期望利润的影响，从图中可以看出来，随着成本预算上限的增加，最优期望利润增加，最终趋于平稳。这是由于当成本预算增加时，带来订购量增加从而导致利润增加的边际效应减小，当达到某一临界值后若继续增加订购量带来的库存过剩成本高于增加订购量带来的利润。同时结果也表明，随着成本约束的增加，利用max-min方法所得的期望利润与需求分布已知情况下获得的期望利润差距逐渐缩小，这也可以说明随着约束成本的增加，max-min准则的鲁棒性也越来越好。此外，与不存在产品数量折扣的情形比较，供应商提供产品数量折扣可带来零售商期望利润的增加。

图1 成本约束变化对最优期望利润的影响

再来看产品需求波动性对最优解的影响。当需求分布信息已知时，Shi和Zhang[21]指出，当产品1需求方差增大时，产品1的最优订货量增大，产品2、3的最优订货量减少；随着产品需求波动性增大，当产品1订货量增大至下一个折扣区间时，订货成本的降低会带来产品1定价减少。图2和图3分别给出了仅知部分需求信息时，产品1方差变化对所有产品最优订货量和最优定价的影响。从图2可以看出，随着产品1需求波动性的增大，该产品的最优订货量逐渐增加，以此减弱需求不确定性对最优期望利润的影响。同时由于约束条件的存在，其他产品的最优订货量会相应有减少，但减少幅度小于产品1订货量的增加；对比图2和图3，可发现与需求分布信息已知的情形类似，当在800到1400之间时，产品1的定价波动较大，且出现了最优定价的减少，这是由于在这一方差波动范围内，产品1的订货量出现了折扣区间的变化，从而导致产品1订购成本的变化。这说明仅知部分需求信息时，产品需求波动性的变化带来各产品最优定价和最优订货量的变化趋势与已知全部需求信息的最优定价和最优订货量的变化趋势是一致的。

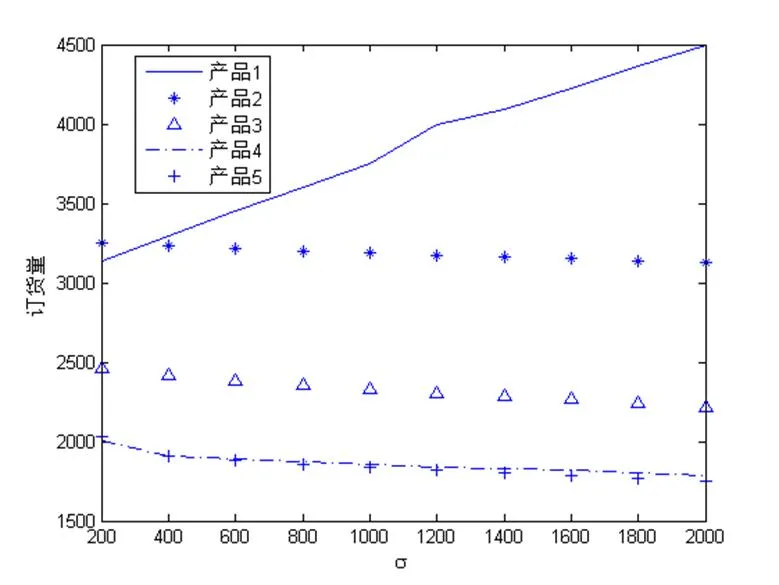
图2 产品1需求标准差变化对订货量的影响

图3 产品1需求标准差变化对定价的影响

4 结论及展望

本文研究了在需求分布未知情况下，存在资源约束和数量折扣的多产品报童模型的库存与定价联合问题，分别考虑了加法需求模式和乘法需求模式两种情况，建立了混合整数非线性规划模型，根据折扣区间限制将问题分解为若干个子问题，针对每一个子问题，利用拉格朗日松弛对约束条件进行处理，证明了目标函数为关于库存因子的凹函数，关于定价的拟凹函数，并得出最优定价和订货量的表达式，在此基础上设计算法对问题进行求解。此外，考虑了需求具体分布未知而仅知随机需求扰动项的均值和方差的情形，利用Scarf[22]提出的最大化最坏情况下利润的max-min准则，求解最坏分布下的最优期望利润。数值算例表明，在需求分布未知的情况下采用max-min准则与利用非实际分布估计得到的最优解相比，具有更好的鲁棒性。供应商提供数量折扣也会带来零售商订货量的增加，而采购成本的降低也会促使零售商选择较低的售价来增加消费者需求，因此供应商和零售商均可从产品数量折扣中获益。此外，提高成本约束会带来期望利润的增加，但边际效应逐渐减弱；产品波动性的增大会导致订货量的增加，当订货量数量增加至下一个折扣区间时，在一定范围内会带来最优定价的减少。

本文的研究仅限于单约束的情况，后续研究可将模型拓展到多个约束条件的情形，并考虑其他更一般的分布，对max-min准则的鲁棒性加以进一步的说明。此外，还可通过设计大规模算例对算法的效率进行评价。

[1] 周永务, 王圣东. 库存控制理论与方法[M]. 北京: 科学出版社, 2009.

[2] Khouja M. The newsboy problem with multiple discounts offered by suppliers and retailers[J]. Decision Sciences, 1996, 27(3): 589-599.

[3] Hadley G, Whitin TM. Analysis of inventory systems[M]. NJ: Prentice Hall, 1963.

[4] Lau HS, Lau AHL. The multi-product multi-constraint newsboy problem: Applications, formulation and solution[J]. Journal of Operations Management, 1995, 13(2): 153-162.

[5] Lau HS, Lau AHL. The newsstand problem: A capacitated multiple-product single-period inventory problem[J]. European Journal of Operational Research, 1996, 94(1): 29-42.

[6] Abdel-Malek LL, Montanari R. An analysis of the multi-product newsboy problem with a budget constraint[J]. International Journal of Production Economics, 2005a, 97(3): 296-307.

[7] Abdel-Malek LL, Montanari R. On the multi-product newsboy problem with two constraints[J]. Computers & Operations Research, 2005b, 32(8): 2095-2116.

[8] Abdel-Malek LL, Areeratchakul N. A quadratic programming approach to the multi-product newsvendor problem with side constraints[J]. European Journal of Operational Research, 2007, 176(3): 1607-1619.

[9] Niederhoff JA. Using separable programming to solve the multi-product multiple ex-ante constraint newsvendor problem and extensions[J]. European Journal of Operational Research, 2007, 176(2): 941-955.

[10] Zhang B, Xu X, Hua Z. A binary solution method for the multi-product newsboy problem with budget constraint[J]. International Journal of Production Economics, 2009, 117(1): 136-141.

[11] Whitin TM. Inventory control and price theory[J]. Management Science, 1955, 2(1): 61-68.

[12] Lau AH, Lau HS. The newsboy problem with price-dependent demand distribution [J]. IIE Transactions, 1988, 20(2): 168-175.

[13] Polatoglu LH. Optimal order quantity and pricing decisions in single-period inventory systems[J]. International Journal of Production Economics, 1991, 23(1): 175-185.

[14] Petruzzi N, Dada M. Pricing and the newsvendor problem: A review with extensions [J]. Operations Research, 1999, 47(2): 184-194.

[15] Murray CC, Gosavi A, Talukdar D. The multi-product price-setting newsvendor with resource capacity constraints[J]. International Journal of Production Economics, 2012, 138(1): 148-158.

[16] Snyder LV, Shen ZJM. Fundamentals of supply chain theory[M]. NJ: John Wiley & Sons, 2011.

[17] Pantumsinchai P, Knowles TW. Standard container size discounts and the single-period inventory problem[J]. Decision Sciences, 1991, 22(3): 612.

[18] Khouja M. The newsboy problem under progressive multiple discounts[J]. European Journal of Operational Research, 1995, 84(2): 458-466.

[19] Khouja M, Mehrez A. A multi-product constrained newsboy problem with progressive multiple discounts[J]. Computers & Industrial Engineering, 1996, 30(1): 95-101.

[20] Zhang G. The multi-product newsboy problem with supplier quantity discounts and a budget constraint[J]. European Journal of Operational Research, 2010, 206(2): 350-360.

[21] Shi J, Zhang G. Multi-product budget-constrained acquisition and pricing with uncertain demand and supplier quantity discounts[J]. International Journal of Production Economics, 2010, 128(1): 322-331.

[22] Scarf H. A min-max solution of an inventory problem[A]. In: Arrow KJ, Karlin S and Scarf H, editors, Studies in Mathematical Theory of Inventory and Production[C], CA: Stanford University Press, 1958: 201-209.

[23] Perakis G, Roels G. Regret in the newsvendor model with partial information[J]. Operations Research, 2008, 56(1): 188-203.

[24] Qiu R, Shang J, Huang X. Robust inventory decision under distribution uncertainty: A CVaR-based optimization approach[J]. International Journal of Production Economics, 2014, 153: 13-23.

[25] Raza SA. A distribution free approach to newsvendor problem with pricing[J]. 4OR, 2014, 12(4): 335-358.

[26] Moon I, Gallego G. Distribution free procedures for some inventory models[J]. Journal of the Operational Research Society, 1994, 45(6): 651-658.

[27] Khouja M. The newsboy problem with multiple discounts offered by suppliers and retailers[J]. Decision Sciences, 1996, 27(3): 589-599.

[28] Vairaktarakis GL. Robust multi-item newsboy models with a budget constraint[J]. International Journal of Production Economics, 2000, 66(3): 213-226.

[29] Moon I, Silver EA. The multi-item newsvendor problem with a budget constraint and fixed ordering costs[J]. Journal of the Operational Research Society, 2000, 51(5): 602-608.

[30] Godfrey GA, Powell W B. An adaptive, distribution-free algorithm for the newsvendor problem with censored demands, with applications to inventory and distribution[J]. Management Science, 2001, 47(8): 1101-1112.

[31] Abdel-Malek L, Montanari R, Morales LC. Exact, approximate, and generic iterative models for the multi-product newsboy problem with budget constraint[J]. International Journal of Production Economics, 2004, 91(2): 189-198.

[32] Chen M, Chen ZL. Recent developments in dynamic pricing research: multiple products, competition, and limited demand information[J]. Production and Operations Management, 2015, 24(5): 704-731.

[33] Gallego G, Moon I. The distribution free newsboy problem: review and extensions[J]. Journal of the Operational Research Society, 1993, 44(8): 825-834.

The Distribution-Free Multi-Products Ordering and Pricing Problem with Quantity Discounts and Resource Constraint

ZHANG Wen-si, LI Jin-lin, WANG Jian-cai, RAN Lun

(School of Management and Economics, Beijing Institute of Technology, Beijing 100081, China)

As a building block of stochastic inventory theory, the newsvendor model has been extensively studied in recent years. The common variants of the classical newsvendor model include multi-products newsvendor problem with recourse constraint, joint ordering and pricing issue, problem with supplier providing quantity discounts, etc. Most of these studies assume that a decision maker understands distribution information of customer demand while making decision. However, this assumption may not be always true. It is more likely to access to limited information of stochastic demand distribution based on historical data. Therefore, newsvendor issue with partial demand information is worth dealing with.

This paper investigates a distribution-free, multi-products ordering and pricing newsvendor problem with suppliers providing all unit quantity discounts. This paper assumes that the expected demand is a decreasing function of the selling price and the only information of stochastic demand shock that the newsvendor can obtain are its mean and variance. The objective of this problem is to find the optimal ordering quantity and selling price for each product in order to maximize the total expected profit and meet with resource constraint. Since the stochastic demand depends on the selling price, two types of demand functions, additive and multiplicative, are taken into consideration, in order to facilitate our analysis.

Firstly, a mixed integer non-linear programming (MINLP) model is developed to formulate the original problem. Since only mean and variance of demand shock are accessible, we can derive the worst case given order quantity for each product, i.e., the lower bound of the expected profit. Then, we employ the max-min criterion to obtain the optimal order quantity by maximizing the lower bound, which are subject to resource constraint.

The existence of resource constraint motivates us to consider the dual problem of the original that involves Lagrange multipliers for the constraint. For a given value of Lagrange multiplier, the Lagrange relaxation method can provide an upper bound for the original problem. In order to obtain the optimal solution, the problem is decomposed into sub-problems according to discount segments of different products. The solution shows that the objective function is concave with respect to the stocking factor and quasi-concave with respect to selling price, and the expression of optimal solution is easily deduced. Bisection iteration algorithm is used to find the optimal Lagrange multiplier. In view of the possible non-optimality of the obtained solutions, a feasibility algorithm is designed to adjust the solutions until the constraint is tight.

Finally, numerical results demonstrate that the robustness and effectiveness of the max-min criterion. What’s more, the results also indicate the quantity discounts provided by supplier can lead to higher ordering quantity of retailer. The retailer will choose a lower selling price after the purchase cost decreases. This study is concluded with a sensitivity analysis of constraint and demand variance as well as their economic implication and managerial insight.

distribution-free; multi-products; ordering; pricing; quantity discount

中文编辑：杜 健；英文编辑：Charlie C. Chen

C931.1, O227

A

1004-6062(2016)04-0210-11

10.13587/j.cnki.jieem.2016.04.027

2015-12-16

2016-01-24

国家自然科学基金重点资助项目（71432002）；国家自然科学基金资助项目（71172172，71272058）；高等学校博士学科点专项科研基金资助项目（20121101110054）

张文思（1990—），女，山东德州人；北京理工大学管理与经济学院博士研究生，研究方向：服务运营管理，库存管理。