激光模式的分类
2016-06-05文伟邓晓鹏施振刚
文伟,邓晓鹏,施振刚
(怀化学院机械与光电物理学院,湖南怀化418008)
激光模式的分类
文伟,邓晓鹏,施振刚
(怀化学院机械与光电物理学院,湖南怀化418008)
由于激光光学的快速发展,激光场的模式被深入的研究,由此产生了众多的激光束.本文总结了这些激光束的命名方法,提出可从四个方面进行归类:用描述光场结构的数学函数来命名的、唯象的用其横模场的形状命名的、用光束的显著特性命名以及用光束的调控手段命名.我们的模式分类尝试对学习和研究激光光学的学生和科研工作者掌握复杂多样的激光横向模式有一定的启发作用.
激光束;横向模式;分类
1 引言
光学历史悠久,光辐射的存在要早于原子、分子、凝聚体等物质.人类出现后,光辐射为人类的一切活动提供能量,是我们体验这个世界的基础.1960年,美国科学家梅曼在爱因斯坦、汤斯和肖洛等人理论的基础上发明了世界上第一台光激射器[1],这之后光学发展进入了新阶段,一般称之为现代光学时期.
激光光学是现代光学很重要的分支,主要研讨激光束在谐振腔、光学系统和其他介质中的传输变换规律[2].在激光光学发展初期,主要是研究光强度呈高斯正态分布的激光束在各种光学系统及其他介质中的传输与变换规律.后来,随着激光传输理论的快速发展,人们希望能准确地描述光场的存在形式,以便更精确的实现对激光的控制和利用.多年来,科研工作者提出了诸多模型来描述各种不同的激光场模式,具有新颖空间分布特性的光场也越来越多.目前,还没有统一的标准对这些新颖光场进行命名,因而各种称谓混杂.
2 激光横向模式的分类
麦克斯韦方程组是电磁统一的标志性成果.光本质上是一种电磁波,因此所有的光学现象都可以用麦克斯韦方程组来统治.由麦克斯韦方程组结合物质方程,可以得到对光辐射其主要作用的亥姆霍兹方程,该方程是光波传播的基本微分方程,它建立了空间某一点的光场与其附近光场之间的关系.高斯光束即为亥姆霍兹方程在缓变振幅近似下的一个特解,也是一般激光器出射光场很好的近似.后来,基于不同的边界条件,人们得到了各种各样区别于高斯光束的激光模式.下面我们试图将这些激光光场模式的命名做一个简单的归类,以期为学习和研究激光光学的学生和科研工作者厘清众多的激光横向模式提供借鉴.
综合诸多文献,我们认为激光光场的模式大致从以下几个方面来命名:
2.1 用描述光场结构的数学函数来命名
除了高斯光束外,厄米-高斯光束[3]和拉盖尔-高斯光束[4]也是傍轴波动方程的正交本征解,分别对应于腔反射镜为矩形(轴对称)和圆形(旋转对称)的情况.厄米-高斯光束可简单的表述为:
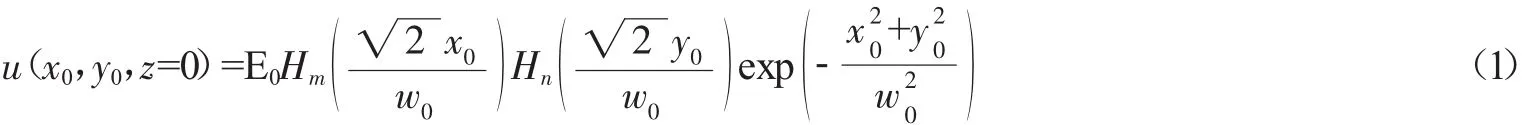
式中Hm(·)即为厄米多项式.而拉盖尔-高斯光束则可简单的表述为:

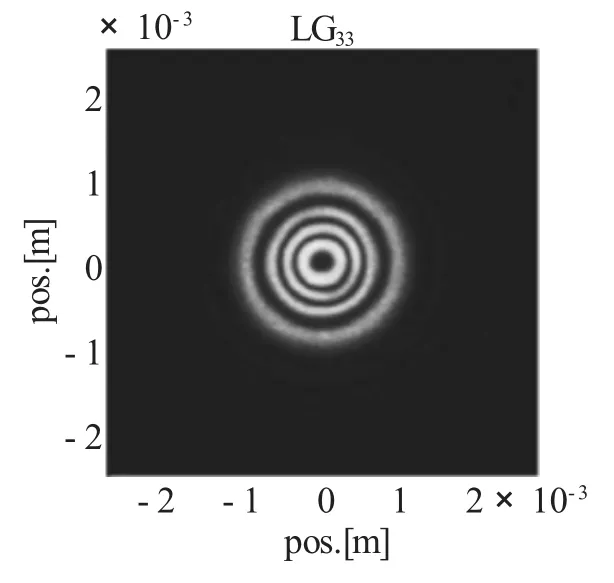
图1 拉盖尔-高斯光束的光场分布

图2 自加速Airy光束的二维(a)及三维图像(b)
1992年,荷兰莱顿大学的L.Allen等人意识到光涡旋携带轨道角动量,随及引发光学界的广泛关注并促使涡旋光场成为光学前沿之一.
最近比较令人关注的以数学函数命名的结构光场是艾里光束[5],其数学表述为:

式中Ai(·)即为特殊函数艾里函数.二维和三维艾里光束的光场分布如图2所示.
除了以上典型的以数学函数命名的激光模式外,其他还有诸多模式,例如:贝塞尔[6]及贝塞尔-高斯光束[7]、厄米-正弦-高斯[8]类光束(包括双曲余弦高斯及余弦-高斯光束)、超高斯光束,马丢[9]及马丢高斯光束、因斯光束、亥姆霍兹-高斯及广义亥姆霍兹-高斯光束、拉普拉斯高斯光束、洛伦兹光束[10]、超几何及超几何高斯光束、笛卡尔光束、Pearcey光束、瓦尼尔-斯塔克光束及厄米-拉盖尔-高斯光束[11]等等.
2.2 唯象的用其横模场的形状命名
有一些激光束模式的场分布不适合简单的用某一个数学函数来表述.比如在惯性约束聚变实验中,为有效抑制高温等离子体的瑞利-泰勒不稳定性,要求入射的激光对特定的靶面区域辐照的光强分布尽可能均匀,因此人们提出了平顶光束的模式分布.在理论研究中,研究者提出了多种数学表述方法,他们都统一的称其为平顶光束,因为这样更简单.用这种方法命名的至少还包括:六边形光束、花瓣状光束[12]及四花瓣光束、狭缝状光束、空心光束(也称暗中空光束)家族[13](包括面包圈光束、中空高斯光束、环形光束及异常空心光束等)、菊花图案光束、叉形光束[14]、瓶状光束[15]、锥形光束[16]、抛物线光束[17]及正多边形光束[18]等等;
2.3 用光束的显著特性命名
空间有限大小的激光模式,由于携带了各个角度的传播分量,在真空或均匀介质中线性传播时能量总是趋于发散分布,称为光束的衍射.然而,1987年美国科学家却提出了无衍射激光束的概念,引起了人们极大的关注.该光束模式实际上就是我们前面提到的贝塞尔光束,它是自由空间标量波动方程的一组特殊解,其场分布具有第一类零阶贝塞耳函数的形式,光场结构与传输距离无关,因此传输中光场结构不变.显然,贝塞尔光束的称谓生僻拗口,而无衍射光束的命名更容易被人们接受.后来,有学者为了避免该称谓与光的衍射本性的冲突提出传输不变光束的概念[19],我们认为更合理.借鉴该方法命名的还包括:自加速光束[5]、自聚焦光束[20]、牵引光束[21-23]以及自相似光束[24、25]等等.这些激光模式的命名往往能激发人们无限的遐想,从而也会推动相关研究工作的快速发展.比如说牵引光束的命名就很能吸引人们的眼球.牵引光束实际上是一种行波,通过光力可以牵引粒子朝向光源运动,实现微粒的长距离逆光传输,其原理现在已经基本得到科学家的共识.但要实现像《星际迷航》和其他影片中显示的那样利用光束牵引飞船和其他大型物体,恐怕还有相当长的路程.图3为假想的利用激光束牵引物体的示意图.

图3 牵引光束假想示意图
2.4 用光束的调控手段命名
比如:调控位相的涡旋光束[4]、调控相干性的部分相干光束(包括高斯-谢尔模光束[26]与各种特殊关联光束[27])以及调控偏振态的矢量光束[28、29](包括径向偏振光[30]和角向偏振光[31]等)等等.
3 结语
以上我们从四个方面对激光束进行了简单分类.当然,以上命名手段不是独立的,比如无衍射光束主要就是指贝塞尔光束或者马丢光束.同时,还有一些是综合命名的,这里不一一列举.
以上激光模式中,我们认为最具代表性的主要有三种:(一)1992年,荷兰科学家L.Allen等发现拉盖尔高斯光束具有轨道角动量,这是光场调控历史上的一个突破性进展,光轨道角动量及光学涡旋产生的力学效应加速了光镊技术的发展,产生的大量的实际应用;(二)1987年美国科学家提出的无衍射贝塞尔光束,在激光精密加工、切片、微调、成像和生物领域有众多的应用;(三)2007年美国科学家提出的自加速激光束,它在光学清扫、等离子体科学、电子加速和微粒操控等领域有重要应用.
各种不同的激光模式在科学发展和技术应用中都不断发挥着重要作用,其产生的新效应和新应用已经在通信、军事、医学等领域产生了深远影响.比如2012年,美国科学家J.N.Clark用相干调控光场进行衍射成像,得到的图像比完全相干的激光成像图像清晰[32].美国中佛罗里达大学的科学家将相干调控光场用于贝尔测量[33]. 2013年,英国格拉斯哥大学的迈尔斯·帕吉特领导的小组发明了利用涡旋位相调控技术检测自旋目标物体的方法[34].美国波士顿大学的科学家发现涡旋位相调控的扭曲光束可以用来编码信息,从而有效地缓解网络拥堵等等[35].2014年,德国科学家将偏振调控光场用于微纳结构中光场振幅和相位的重构[36].最近发现贝塞尔光束即使是在空气或真空中传播时,光速也低于通常认为的299792458米/秒[37],这让我们得以用一种全新的方式思考这些特殊的激光模式的特性.可见,对激光模式的研究具有重要的理论和实用价值,是蓬勃发展的研究领域.
[1]T.H.Maiman.Stimulated optical radiation in ruby[J].Nature,1960,187:493-494.
[2]吕百达.激光光学:光束描述、传输变换与光腔技术物理[M].北京:高等教育出版社,2003.
[3]A.E.Siegman.Hermite-Gaussian functions of complex argument as optical-beam eigenfunc-tions[J].J.Opt.Soc.Am,1973,63(9):1093-1094.
[4]L.Allen,M.W.Beijersbergen,R.J.C.Spreeuw,et al.Orbital angular momen-tum oflight and the transformation ofLaguerre-Gaussian laser modes[J].Phys.Rev.A.,1992,45(11):8185-8189.
[5]G.A.Siviloglou,J.Broky,A.Dogariu,et al.Observation of Accelerat-ing Airy Beams[J].Phys.Rev.Lett,2007,99(21):213901.
[6]J.Durnin,Jr.J.J.Miceli,and J.H.Eberly.Diffraction-free beams[J].Phys.Rev.Lett,1987,58(15):1499-1501.
[7]F.Gori,G.T.Guattari,and C.Padovani.Bessel-gaussian beams[J]. Opt.Commun,1987,64(6):491-495.
[8]L.W.Casperson and A.A.Tovar.Hermite-sinusoidal-Gaussian beams in complex optical systems[J].J.Opt.Soc.Am.A,1998,15(4):954-961.
[9]J.C.Gutiérrez-Vega,M.D.Iturbe-Castillo and S.Chávez-Cerda.Alternative formulation for invariant optical fields:Mathieu beams[J].Opt.Lett,2000,25(20):1493-1495.
[10]O.El Gawhary and S.Severini.Lorentz beams and symmetry properties in paraxial optics[J].J.Opt.A:Pure Appl.Opt,2006,8(5):409-414.
[11]D.Dengand Q.Guo.Elegant Hermite-Laguerre-Gaussian beams [J].Opt.Lett,2008,33(11):1225-1227.
[12]G.Grynberg,A.Maitre,and A.Petrossian.Flowerlike patterns generated by a laser beam transmitted through a rubidium cell with single feedback mirror[J].Phys.Rev.Lett.,1994,72(15):2379-2382.
[13]J.Yin,W.Gao and Y.Zhu.Generation of dark hollow beams andtheir applications[J].Prog.Opt.,2003,45:119-204.
[14]P.Saari and K.Reivelt.Evidence of X-shaped propagationinvariant localized light waves[J].Phys.Rev.Lett.,1997,79(21):4135-4138.
[15]J.Arlt and M.J.Padgett.Generation of a beam with a dark focus surrounded[J].Opt.Lett.,2000,25(4):191-193.
[16]A.V.Shchegrov and E.Wolf.Partially coherent conical beams[J]. Opt.Lett.,2000,25(3):141-143.
[17]M.A.Bandres and J.C.Gutiérrez-Vega.Parabolic nondiffracting optical wave fields[J].Opt.Lett.,2004,29(1):44-46.
[18]S.Barwick.Accelerating regular polygon beams[J].Opt.Lett.,2010,35(24):4118-4120.
[19]J.Turunen and A.T.Friberg.Propagation-invariant optical fields [J].Prog.Opt.,2010,54:1-88.
[20]N.K.Efremidis and D.N.Christodoulides.Abruptly autofocusing waves[J].Opt.Lett.,2010,35(23):4045-4047.
[21]J.Chen,J.Ng,Z.Lin,and C.T.Chan.Optical pulling force[J].Nat. Photon.,2011,5(9):531-534.
[22]A.Novitsky,C.-W.Qiu and H.Wang.Single gradientless light beam drags particles as tractor beams[J].Phys.Rev.Lett.,2011,107(20):203601.
[23]D.B.Ruffne and D.G.Grier.Optical conveyors:a class of active tractor beams[J].Phys.Rev.Lett.,2011,109(16):163903.
[24]G.P.Karman,G.S.McDonald,G.H.C.New,et al.Laser optics:Fractal modes in unstable resonators[J].Nature,1999,402:138.
[25]N.Gao and C.Xie.Free space self-similar beams[J].Opt.Lett.,2015,40(7):1216-1219.
[26]E.Wolf and E.Collett.Partially coherent sources which produce the same far-field intensity distribution as a laser[J].Opt. Commun.,1978,25(3):293-296.
[27]Y.Cai,Y.Chen and F.Wang.Generation and propagation of partially coherent beams with nonconventional correlation functions:a review[J].J.Opt.Soc.Am.A,2014,31(9):2083-2096.
[28]Q.Zhan.Cylindrical vector beams from mathematical concepts to applications[J].Adv.Opt.Photon.,2009,1(1):1-57.
[29]X.-L.Wang,J.Chen,Y.Li,etal.Opticalorbitalangular mo-mentum from the curl of polarization[J].Phys.Rev.Lett.,2010,105(25):253602.
[30]R.Dorn,S.Quabis and G.Leuchs.Sharper focus for a radially polarized light beam[J].Phys.Rev.Lett.,2003,91(23):233901.
[31]K.S.Youngworth and T.G.Brown.Focusing of high numerical aperture cylindrical-vector beams[J].Opt.Express,2000,7(2):77-87.
[32]J.N.Clark,X.Huang,R.Harder,et al.High-resolution threedimensional par-tially coherent diffraction imaging[J].Nat. Comumn.,2012,3(8):993.
[33]K.H.Kagalwala,G.D.Giuseppe,A.F.Abouraddy,et al.Bell's measure in clas-sical optical coherence[J].Nat.Photon.,2013,7(1):72-78.
[34]M.P.J.Lavery,F.C.Speirits,S.M.Barnett,et al.Detection of a spinning object using light’s orbital angular momentum[J]. Science,2013,341:537-540.
[35]N.Bozinovic,Y.Yue,Y.Ren,et al.Terabit-scale orbital angular momentum mode division multiplexing in fibers[J].Science,2013,340:1545-1548.
[36]T.Bauer,S.Orlov,U.Peschel,P.Banzer,et al.Nanointerferometric amplitude and phase reconstruction of tightly focused vector beams[J].Nat.Photon.,2013,8(1):23-27.
[37]D.Giovannini,J.Romero,V.Potocˇek,et al.Photons that travel in free space slower than the speed of light[J].Science,2015,347:857-860.
Investigation on the Classification of Laser Modes
WEN Wei,DENG Xiao-peng,SHI Zhen-gang
(School of Mechanical,Optics and Physics,Huaihua University,Huaihua,Hunan 418008)
Due to the rapid development of laser optics,laser field modes are in-depth researched and many laser beams are dis-covered.There are four classifications for those laser field modes:the laser beams were named for the mathematical function which describes the structure of the light field.The laser beams were named for the shape of the light field,the laser beams were named for the distinctive character of the light field and the laser beams were named for the manipulation ways of the light field.Our results may be useful for the students and researchers who study and research laser optics to grasp the complicated laser modes.
laser beam;transverse laser-mode;classification
0436
A
1671-9743(2016)11-0035-04
2016-06-04
国家自然科学基金(No.11474120;11374222);湖南省教育厅一般项目(No.14C0896).
文伟,1978年生,湖南张家界人,博士,副教授,研究方向:激光束的传输与调控,统计光学,大气光学等.
