孤立波对直立防波堤波浪渗流作用的解析计算*

莫弼川，周文丰，黄 华，詹杰民，朱梦华

(中山大学工学院，广东 广州 510275)

孤立波对直立防波堤波浪渗流作用的解析计算*

莫弼川，周文丰，黄 华，詹杰民，朱梦华

(中山大学工学院，广东 广州 510275)

浅水波浪在一定条件下可能以孤立波形态与近岸海工设施产生相互作用。该文基于水波反射理论和波浪渗流的Biot固结理论，应用特征函数法，推导了孤立波作用下直立防波堤的反射波速度势和波浪引起的海床内渗流压力分布的解析表达式，并据此计算了作用于直立防波堤底部的由孤立波渗流压力所致浮托力和倾覆力矩。计算结果表明海况与海床条件以及防波堤几何条件等因素的变化对孤立波引起的渗流浮托力和倾覆力矩均有一定影响。在一定条件下，对防波堤的孤立波渗流作用与孤立波直接作用量级相近。与微幅波理论相比，孤立波理论有效反映了浅水波非线性特征的影响。

孤立波；直立防波堤；波浪反射；波浪力；渗流浮托力和倾覆力矩

防波堤在港口和海岸防中应用得十分广泛，其主要功能是防御波浪对港口的侵袭和破坏，从而保证水面平稳，改善船舶停泊和作业条件[1]。常见的防波堤形式有直立式，斜坡式，浮式，圆顶和圆弧式等，其中直立重力式结构是最常用的形式之一。其稳定性不仅取决于自身的重量和波浪力的冲击力，还与可渗透弹性海床上渗流作用产生的浮托力和倾覆力矩密切相关。

实际工程中，直立式防波堤主要用于浅水区域。在浅水区，波浪的波高和水深之比和波长和水深之比增大导致波浪非线性程度增加，继续使用线性Airy波模型将产生一定的误差。因此在浅水波波长充分大的时候，需要引入孤立波模型对波浪荷载作用进行描述。Isaacson[2]采用孤立波模型对墩柱进行绕射问题的研究。苏铭德等[3]对孤立波对柱群的绕射作用进行了分析。刘长根等[4]就孤立波与不同淹没深度水平圆柱体的相互作用问题展开了相关研究。缪国平等[5]对二维浮体上孤立波透射与反射进行了解析研究。Zhong等[6]推广了Isaacson的方法，研究了孤立波对透空圆环柱的作用效果。Williams等[7]研究了线性Airy波和透空柱群的相互作用情况。

另一方面，当防波堤固立于可渗透海床上时，波浪将在海床内产生往复的波浪水压力，使得海床内土体超静空隙水压力上升乃至液化，形成海床内渗流压力场。所以除考虑波浪直接作用外，一般还需要考虑波浪引起的渗流对防波堤的作用力[8]。孙昭晨等[9]给出了固立于有限厚度海床上的圆墩柱的波浪渗流压力分布解析解。李奇等[10-11]研究了椭圆余弦波和孤立波引起的对固立墩柱底部的波浪渗流作用。黄华等[12-13]研究了二层海洋中大直径密实柱和透空圆环柱底部的波浪渗流作用效果。邹志利等[14]采用Airy波模型对直立式防波基底堤进行了波浪渗流解析研究。Zhu等[15]进一步研究了透空直立防波堤在二层海洋条件下的渗流作用。

本文将孤立波模型引入到对直立防波堤波浪渗流作用的研究之中，首先对直立防波堤的孤立波反射波浪场进行了解析分析，推导给出了孤立波反射波势与波浪压力算式。进一步将波浪渗流问题的Biot固结理论推广应用于孤立波作用问题，推导了由孤立波引起的对应有限厚度直立防波堤的海床内渗流压力分布解。并据此对波浪渗流浮托力和倾覆力矩进行了实算，从而揭示了对应防波堤的孤立波波浪渗流作用的各种变化规律。相关结果对于近岸海工固立结构的波浪渗流作用的深入研究以及对防波堤的设计与应用均具有理论和实际的参考价值。

1 孤立波对防波堤的反射问题解

对于大尺度直立防波堤，边界层厚度较小，海水可视为无粘流体，且运动无旋，波浪对密实防波堤的影响主要为水波的反射作用。进一步考虑防波堤固立于可渗透弹性海床上，根据Biot固结理论和相关假设[8]，可以设定立于海床上结构与海床间无相对滑动，海床内土体各向同性、可渗透且具有弹性性质，而海床底部不可渗透和无变形。由于一般情况下海床的渗流速度远小于海底波浪场的水流速度，故在孤立波反射波浪场求解中可以不考虑海床对其的影响。

如图1所示，设z为垂直方向变量，x为水平方向变量，o为坐标原点，水深为d，海床厚度为h，直立防波堤厚度为b，另设波高为H。图1中波浪场记为Ω1，对应的防波堤底部海床渗流压力场可划分为V1，V2和V3三个区域。

图1 固立于海底可渗透弹性海床上的直立防波堤Fig.1 Vertical breakwater resting on the permeable elastic seabed

首先对浅水波KdV方程进行求解，可得入射孤立波自由波面表达式[2]：

(1)

式中η为入射孤立波自由表面波，c为孤立波波速，t为时间。考虑孤立波理论上的传播范围为x∈(-∞,+∞)，故可将η函数按变量x作傅里叶积分变换，相应η函数的傅立叶积分逆变换表达式为[2]:

(2)

式中，A(k)为关于孤立波波面的傅立叶积分正变换象函数，k为象函数自变量。设u为入射水波质点的一阶水平方向速度，由浅水波近似理论，可得：

(3)

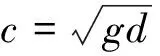
(4)

取Φi=Re(φi)，则有:

(5)

(6)

应用特征函数法，可推得孤立波反射波势为：

(7)

相应总波势为Φ=Re(φ)，其中

(8)

(9a)

(10a)

对比式(1)和式(2)，又可写为：

(9b)

(10b)

2 孤立波引起的渗流作用问题解

将海床内渗流区域划分为为V1，V2和V3三个区域(如图1所示)。设Pw为孤立波引起的海底处的总动水压力，有Pw=Re(pw)，其中pw=pi+pr，pi和pr分别对应入射波动压和反射波动压，且有：

coskxe-ikctd(kb)

(11)

再设海床内渗流区域V1，V2和V3对应的孤立波渗流压力解为：P(j)=Re(p(j))(j=1,2,3)，引入Biot波浪渗流固结理论[8]，渗流场压力对应的边值问题提法为：

(12)

(13)

(14)

(15)

(16)

推广应用特征函数法，对应各区的波浪渗流压力解可取为：

(17)

(18)

(19)

(20)

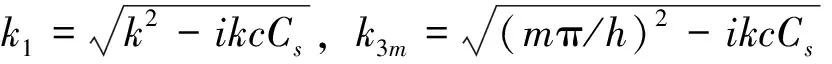
利用渗流区域交界面处匹配条件：

(21)

(22)

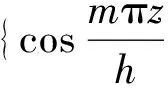
进一步设直立防波堤受到的波浪渗流浮托力和倾覆力矩为Fv=Re(fv)和Mv=Re(mv)，推导可得：

(23)

(24)

(25)

(26)

3 算例与分析

图2和图3描述了直立防波堤所受孤立波波浪力和力矩随相对时间的变化状况。如图所示，随着参数β的增大，水波非线性特征趋强，孤立波波浪力和力矩的时间脉冲变化随之明显趋强，力和力矩在峰值出现的相对时间点附近产生急剧变化。而对应不同参数β，波浪力和力矩峰值保持不变。

图2 无量纲波浪力随相对时间的变化Fig.2 Temporal variation of dimensionless wave force

图4和图5分别给出孤立波渗流引起的作用于直立防波堤底部的浮托力和倾覆力矩随相对时间的变化趋势。由图可见，与水平波浪力和力矩的变化状态相比，随着参数ξ的增大，浮托力和倾覆力矩峰值有所减小，而变化形态相近且相对平缓。相对于倾覆力矩，浮托力随ξ的变化程度更为明显一些。

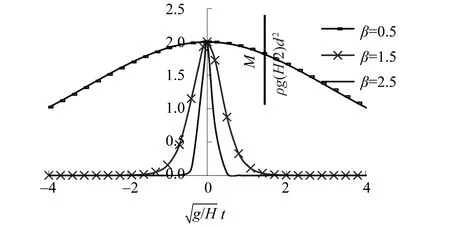
图3 无量纲波浪力矩随相对时间的变化Fig.3 Temporal variation of dimensionless wave moment

图4 无量纲浮托力随相对时间的变化(b/d=2,b/h=1,Cs=0)Fig.4 Temporal variation of dimensionless uplift force

图5无量纲倾覆力矩随相对时间的变化(b/d=2,b/h=1,Cs=0)Fig.5 Temporal variation of dimensionless overturning moment

图6和图7表示在不同综合特性系数Cs的取值下浮托力和倾覆力矩随时间的变化情况。由图可知，随着Cs的增大，浮托力和倾覆力矩的峰值大小有所降低，且峰值对应的相对时间点出现一定程度的延迟。当Cs≠0时，随相对时间变化的振荡态势不再对称。相对于倾覆力矩，浮托力随Cs的变化程度更大。

图6 无量纲浮托力随相对时间的变化(b/d=2,b/h=1,ξ=1)Fig.6 Temporal variation of dimensionless uplift force

图7 无量纲倾覆力矩随相对时间的变化(b/d=2,b/h=1,ξ=1)Fig.7 Temporal variation of dimensionless overturning moment

图8和图9表示了浮托力和倾覆力矩幅值随综合特性系数Cs的变化状况。由图可见，随着Cs值的减小，无量纲浮托力和倾覆力矩幅值均随之增大，Cs为零对应最大渗流力和力矩幅值。由此说明在需要考虑孤立波渗流作用的防波堤实际设计中，按照工程安全规则，可取Cs=0，即不考虑土介质的变形和孔隙水的压缩性。这与微幅波渗流理论的相关结论趋于一致[8]。

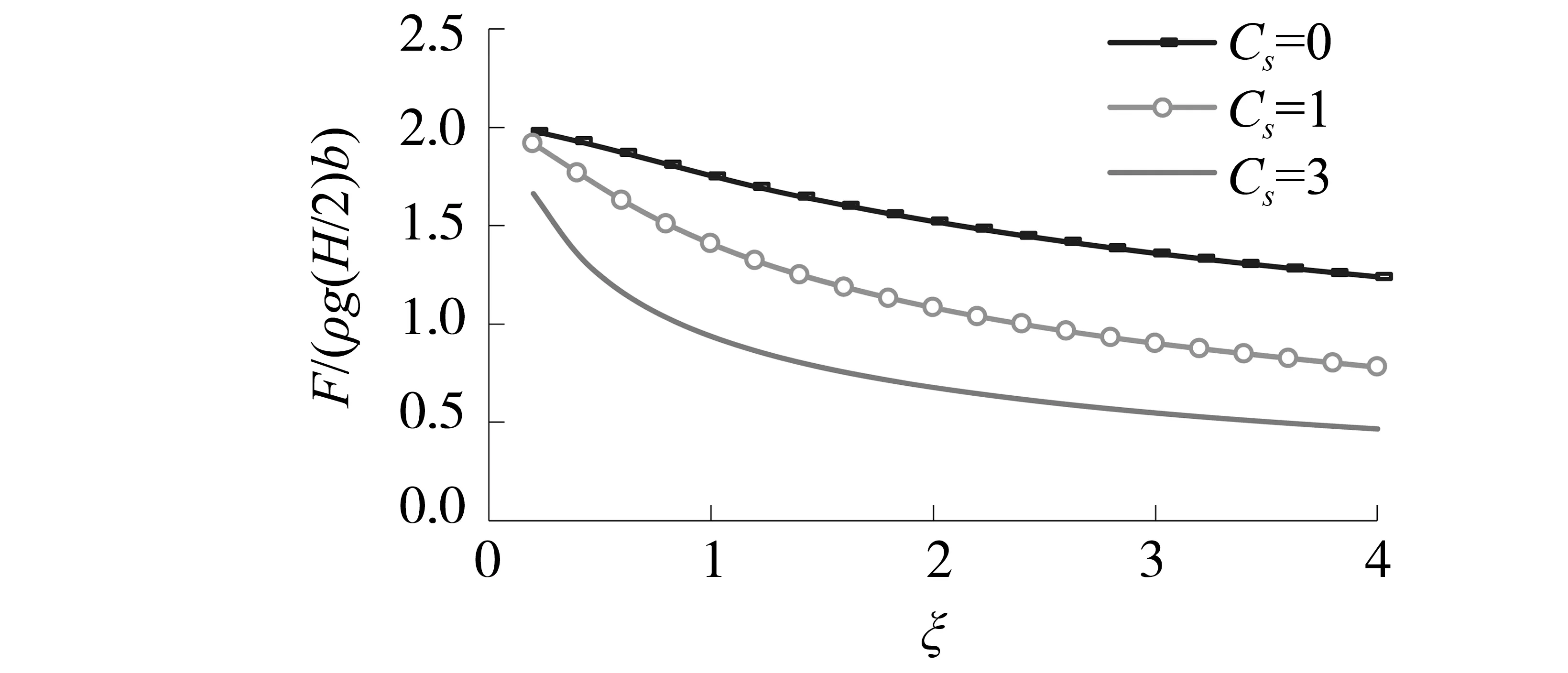
图8 无量纲浮托力幅值随Cs的变化(b/d=2,b/h=1)Fig.8 Comparison of uplift force for differentCs

图9 无量纲倾覆力矩幅值随Cs的变化(b/d=2,b/h=1)Fig.9 Comparison of overturning moment for different Cs

图10至图13为Cs=0时波浪力和浮托力幅值以及波浪力矩和渗流倾覆力矩幅值的对比图。由图可知，随着无量纲参数ξ的增大，浮托力和倾覆力矩幅值均呈现出平稳下降的趋势，而波浪力和波浪力矩幅值保持不变。进一步可见，随着参数b/d的增大，渗流浮托力与倾覆力矩幅值可以分别接近甚至超过水平波浪力与波浪力矩幅值，说明在一定的浅水和海床条件下，孤立波引起的对防波堤底部的渗流作用不容忽视。

图10无量纲波浪力与浮托力幅值的比较 (b/d=2,b/h=1,Cs=0)Fig.10 Comparison of dimensionless wave force and uplift force

图11 无量纲波浪力矩和倾覆力矩幅值的比较(b/d=2,b/h=1,Cs=0)Fig.11 Comparison of dimensionless wave moment and overturning moment

图12 无量纲波浪力与浮托力幅值比较(b/d=3,b/h=1,Cs=0)Fig.12 Comparison of dimensionless wave force and uplift force

图13 无量纲波浪力矩和倾覆力矩幅值的比较(b/d=3,b/h=1,Cs=0)Fig.13 Comparison of dimensionless wave moment and overturning moment

图14和图15反映了无量纲浮托力和倾覆力矩幅值随参数h/b的变化状况。由图可见，随着参数h/b增大，无量纲浮托力和倾覆力矩幅值均呈现轻微的减小。说明一定范围内，海床厚度对渗流作用的影响相对较小

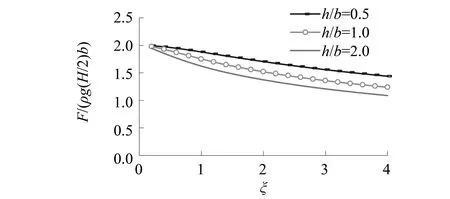
图14 无量纲浮托力幅值随h/b的变化(Cs=0)Fig.14 Comparison of dimensionless uplift force for different h/b

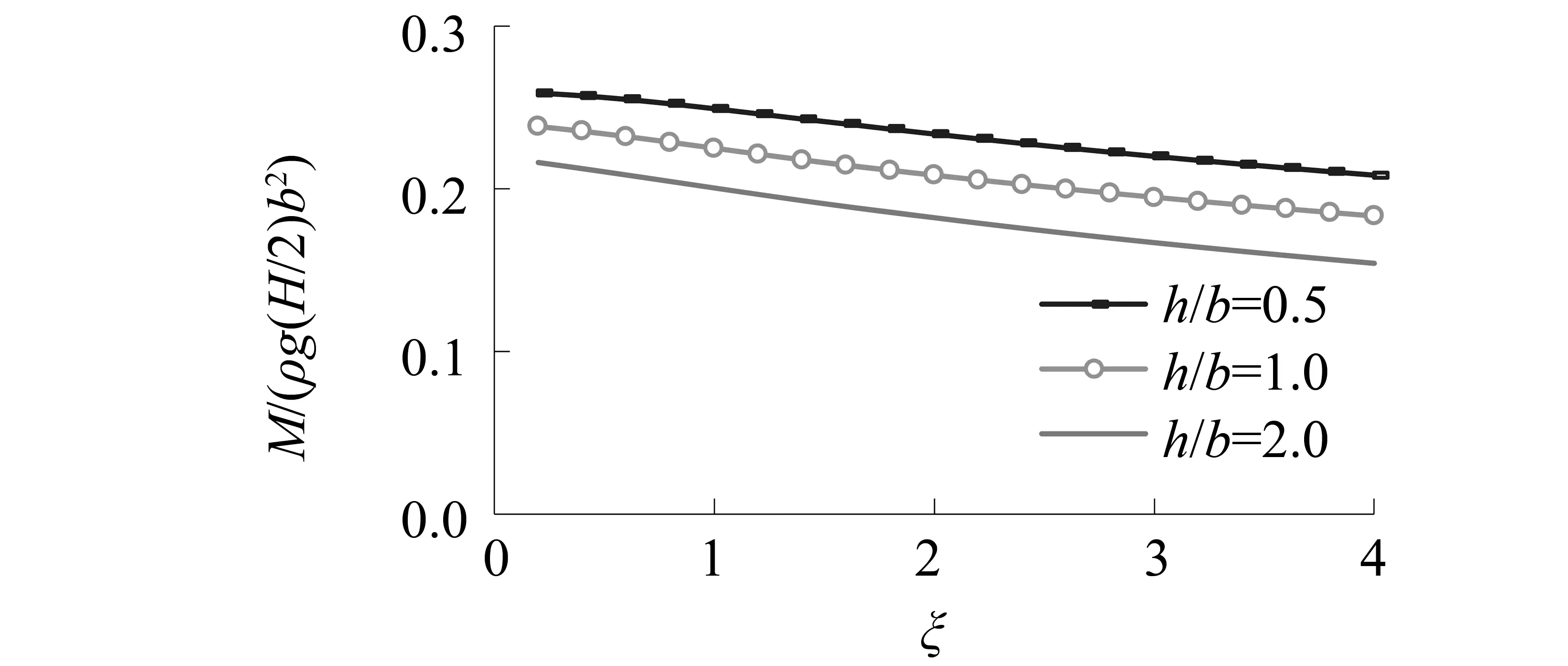
图15 无量纲倾覆力矩幅值随h/b的变化(Cs=0)Fig.15 Comparison of dimensionless overturning moment for different h/b

图16和图17为Cs=0时按Airy微幅波理论对无量纲浮托力和倾覆力矩幅值的计算结果。其中当kd较小时即为浅水条件下Airy微幅波的作用效果。

图16 Airy波无量纲波浪力和浮托力比较(b/d=3,b/h=1,Cs=0)Fig.16 Comparison of dimensionless Airy wave force and uplift force

图17 Airy波无量纲波浪力矩和倾覆力矩比较(b/d=3,b/h=1,Cs=0)Fig.17 Comparison of dimensionless Airy wave moment and overturning moment

将图12与图16，以及图13与图17进行对比，可以发现，在浅水相似条件下，防波堤所受孤立波直接作用和波浪渗流作用均明显大于Airy波理论对应的估值。对此，可据图举例说明。取波高H=2.6m，水深d=6.5m，另取b/d=3，b/h=1，相应有H/d=0.4(符合浅水波一般条件)，ξ=1.9。依据图12与图13以及图16与图17，对应的孤立波作用结果为：最大单位宽水平波浪力约为3.4×105N，最大单位宽水平波浪力矩约为1.1×106N·m；最大单位宽渗流浮托力约为3.9×105N，最大单位宽渗流倾覆力矩约为1.0×106N·m。该结果再次说明，在一定的条件下，孤立波对防波堤的直接作用与波浪渗流作用可能具有相同量级。再依据图16和图17，按Airy微幅波理论，设浅水线性长波波长为L=205m，相应参数kd=0.2(符合Airy浅水波一般条件)，对应结果为：最大单位宽水平波浪力约为1.7×105N，最大单位宽水平波浪力矩约为5.5×105N·m；最大单位宽渗流浮托力约为2.5×105N，最大单位宽渗流倾覆力矩约为5.8×105N·m。该结果与前述结果相比，可见在浅水条件下，按Airy微幅波理论得到的结果相对于孤立波理论将低估约50%，这说明在一定浅水条件下，线性波理论可能不再适用于对防波堤所受波浪作用和渗流作用的预测。

4 结 论

本文将Airy微幅波水波反射理论和Biot波浪渗流固结理论有效加以推广，应用特征函数法，解析推导了孤立波对直立防波堤的反射波势解以及波浪引起的对应可渗透海床内的渗流压力解，并据此对作用于直立防波堤上的波浪力、波浪力矩以及渗流浮托力和倾覆力矩进行了实算，得出如下主要结论：

1)波浪渗流作用随时间的变化关系与波浪直接作用随时间的变化关系存在一定差异。相关参数ξ对渗流载荷的影响明显小于相关参数β对波浪直接作用的影响。随着β的增大，孤立波波浪力和力矩在峰值出现的相对时间点附近产生急剧变化，而渗流浮托力与倾覆力矩不存类似的变化形态。此外，随着综合特性系数Cs的增大，浮托力和倾覆力矩峰值对应的相对时间点将出现一定程度的延迟。

2)在一定的海况条件和防波堤几何条件下，防波堤所受直接波浪力和力矩幅值与波浪渗流引起的浮托力和力矩幅值可以具有相同量级，说明当防波堤需要引入孤立波理论对波浪直接载荷预测时，根据当地海底地质条件，可能还需要对孤立波引起的作用于防波堤底部的渗流载荷加以预测。

3)随着Cs由零逐步增大，无量纲浮托力和倾覆力矩幅值随之减小，说明在实际防波堤渗流作用的计算中，取Cs=0是趋于安全的。

4) 对比孤立波理论和Airy微幅波理论在相同或相似的浅水条件、渗流条件和结构几何条件下的波浪与波浪渗流载荷幅值的计算结果，可以发现：微幅波理论估值明显低于孤立波理论估值，即孤立波理论较好地反映了浅水波的非线性特征，也由此说明一定条件下选取孤立波理论对防波堤进行波浪作用预测更为合理可靠。

[1] 张磊. 直立式防波堤的可靠性分析[D]. 青岛：中国海洋大学, 2011.

[2]ISSACSONMdeStQ.Solitarywavediffractionaroundlargecylinder[J].JournalofWaterwayPortCoastal&OceanEngineering, 1983, 109(1):121-127.

[3] 苏铭德, 潘宇. 浅水中群桩受力状况的理论研究[J]. 应用数学和力学, 1987(4):367-376.

[4] 刘长根, 陶建华. 孤立波与不同淹没深度水平圆柱体的相互作用[J]. 水动力学研究与进展(A辑), 2006, 21(2): 155-160.

[5] 缪国平, 刘应中. 二维浮体上孤立波透射与反射的解析解[J]. 海洋工程, 1992, (3):19-32.

[6]ZHONGZ,WANGKH.Solitarywaveinteractionwithaconcentricporouscylindersystem[J].OceanEngineering, 2006, 33(7): 927-949.

[7]WILLIAMSAN,LIW.Waterwaveinteractionwithanarrayofbottom-mountedsurface-piercingporouscylinders[J].OceanEngineering, 2000, 27(8): 841-866.

[8] 邱大洪，孙昭晨. 波浪渗流力学[M]. 北京: 国防工业出版社, 2006: 193-203.

[9] 孙昭晨，邱大洪.作用于可渗可压缩海床上的墩柱底面上的波浪力[J].海洋学报，1989(3)：364-371.

[10] 李奇, 黄华, 詹杰民,等. 作用于透空圆环墩柱的浅水波绕射波浪力与波浪渗流力[J]. 中山大学学报(自然科学版), 2013，52(3):23-29.

[11] 李奇, 黄华, 詹杰民,等. 孤立波引起的对固立墩柱底部的波浪渗流作用[J]. 热带海洋学报, 2013, 32(5):42-47.

[12] 黄华, 曾昭銮, 詹杰民,等. 二层海中立于可渗透海床上的大直径墩柱的波浪渗流力[J]. 中山大学学报(自然科学版), 2011, 50(2):36-41.

[13] 黄华, 许潇楠, 詹杰民,等. 作用于二层海洋中大直径透空圆环墩柱上的波浪渗流力[J]. 中山大学学报(自然科学版), 2013，52(5):6-13.

[14] 邹志利, 邱大洪. 直立式防波堤基底波浪渗流压力解析解[J]. 水动力学研究与进展, 1992(3):295-302.

[15]ZHUM,HUANGH,ZHANJ,etal.Waveinteractionwithporousverticalbreakwaterintwo-layerfluid[J].ProcediaEngineering, 2015, 126: 218-222.

Analytical calculation of solitary wave-induced seepage effects on the vertical breakwater

MOBichuan,ZHOUWenfeng,HUANGHua,ZHANJiemin，ZHUMenghua

(College of Engineering, Sun Yat-sen University, Guangzhou 510275, China)

In certain condition, the shallow water wave may emerge in solitary wave form, interacting with offshore structures. Based on wave reflection theory and Biot wave seepage consolidation theory, the analytical solutions of the reflected solitary wave potentials and the solitary wave-induced seepage pressures inside permeable elastic seabed are derived by applying the eigenfunction expansion approach, and the wave-induced lift force and overturning moment caused by the seepage pressure on the bottom of the vertical breakwater are accordingly calculated. The results show that the variation of sea and seabed conditions and breakwater geometry condition may have some influence on wave-induced seepage uplift force and overturning moment. The solitary wave-induced seepage effects may have the same order of magnitude as the direct horizontal wave effects. Compared with the results from small amplitude wave theory, the solitary wave theory can reflect shallow wave nonlinear effects.

solitary wave; vertical breakwater; wave reflection; wave force; wave-induced seepage uplift force and overturning moment

10.13471/j.cnki.acta.snus.2016.02.006

2015-11-14

国家海洋公益性行业专项资金资助项目(201005002)

莫弼川(1993年生)，男；研究方向：流体力学；通讯作者：黄华；E-mail:tsyhh1982@163.com

O

A

0529-6579(2016)02-0028-08