海洋柔性立管二维振动的输出反馈控制*
2016-06-05邬依林
盘 川,侯 畅,邬依林
(1. 东北林业大学信息与计算机工程学院,黑龙江 哈尔滨 150040;2. 广东第二师范学院计算机科学系,广东 广州 510310)
海洋柔性立管二维振动的输出反馈控制*
盘 川1,侯 畅1,邬依林2
(1. 东北林业大学信息与计算机工程学院,黑龙江 哈尔滨 150040;2. 广东第二师范学院计算机科学系,广东 广州 510310)
考虑了海洋柔性立管在时变内流和海流作用下二维振动控制问题。柔性立管系统动力学行为由两个偏微分方程和六个常微分方程描述。为提高其振动控制效果并避免控制溢出,直接基于其无限维分布参数模型,利用Lyapunov直接法和高增益观测器技术研发了输出反馈边界控制来控制立管的二维振动。随后证明了海流扰动作用下控制系统的一致最终有界稳定性和闭环状态的一致有界性。最后,仿真结果验证了文中所设计二维输出反馈边界控制算法的有效性。
海洋立管;二维振动;边界控制;输出反馈控制;Lyapunov直接法
海洋立管在海底石油钻探和天然气开发工程中起到至关重要的作用,因此其振动问题也受到越来越多的关注[1-4]。随着资源开采进入深水域,所面临的环境也更加严酷,海洋柔性立管在管内流体和海流等载荷作用下的振动也将更加剧烈。而过多的振动将使立管过早疲劳破坏,这将产生昂贵的维修费用,更为甚者,将会带来严重的环境污染。因此,为了保证海洋立管的生产效率,亟需研发机电控制系统以抑制立管的振动。
近年来,为避免基于模型近似或者离散化方法所产生的控制溢出问题[5-8],海内外很多学者研究了海洋柔性立管的边界控制[1-4, 9-14]。然而,目前国外关于柔性立管的振动控制研究中,却都忽略了内流对立管动力学的影响[9-14]。在国内,笔者前期研究成果设计了诸如PD边界控制、鲁棒边界控制、自适应边界控制、二维边界控制等[1-4],并取得了较好的控制效果,同时也验证了内流动力学的作用能减小立管系统的自然频率。然而,在文献[1-4,9-14]中,作者都假定控制器中的系统状态均可直接由传感器测得或应用差分算法获得。而在实际中,来自传感器的噪声是不可避免的,尤其是那些在对时间微分过程中产生的系统状态,将影响文献[1-4,9-14]中所设计控制器的执行。因此,为了解决这个问题,本文将使用高增益观测器来设计输出反馈边界控制来抑制立管的振动。
本文以耦合内流动力学的海洋柔性立管系统二维振动主动控制为研究对象,基于其原始无穷维分布参数模型,融合Lyapunov综合法和边界控制技术设计了二维输出反馈边界控制用于抑制立管的振动偏移量。此外,高增益观测器用于估计不可测系统状态量,解决了因差分算法来获得系统状态而带来的噪音放大问题,从而提高控制系统的性能。其后,对海流扰动作用下控制系统的一致最终有界稳定性和和闭环状态的一致有界性进行了严格的数学证明。仿真结果进一步验证了本文所设计输出反馈边界控制器的有效性。
1 问题描述
1.1 立管动力学建模
一类典型海洋柔性立管系统如图1所示,其中O为坐标系原点,L为立管长度,w(即w(x,t))和v(即v(x,t))分别为立管的横向和纵向偏移量,Uw(即Uw(t))和Uv(即Uv(t))分别为立管的横向和纵向控制器,f(即f(x,t))为时变海流。
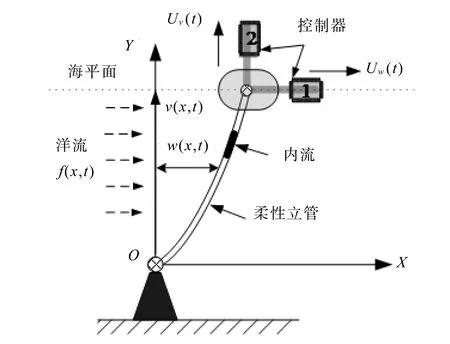
图1 一个典型的海洋柔性立管系统Fig.1 A typical flexible marine riser system
本文所研究立管系统模型将引用研究成果文献[1],即由文献[1]中式(9)-(11)可得本文所研究的柔性立管系统动力学模型为
(1)
其中mr和mf分别为立管单位质量和内流单位质量,Vi为时变内流速度,c1和c2分别为结构横向和纵向阻尼系数,T、EI和EA分别为立管张力、弯曲刚度和轴向刚度,f(x,t)为时变海流干扰载荷,表示为
(2)
其中ρs为海水密度,D为立管外径,β为相位角,AD为阻力振荡部分幅值,CD(即CD(x,t))和Vs(即Vs(x,t))分别为阻力系数和时变海流流速,fv=StVs/D为涡旋脱落频率,St为斯特劳哈尔数。
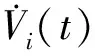
1.2 预备知识
为方便随后章节的工作,本小节将列出如下引理[7-8]。
引理1 设φ1(x,t),φ2(x,t)∈R,σ>0其中x∈[0,L],t∈[0, +∞),下列不等式成立
(3)
引理2 设φ(x,t)∈R为定义在x∈[0,L],t∈[0, +∞)的函数,且满足如下边界条件

(4)
则有如下不等式组成立
(5)
2 控制设计
控制目标是抑制柔性立管在内外流作用下的二维振动。在本节中,我们采用Lyapunov直接法、边界控制技术和高增益观测器在立管上边界构造两个输出反馈边界控制器,并证明闭环系统的一致有界稳定性。
引理3 假设一个系统的输出y(t)和它的n阶微分都是有界的并满足|y(k)|
(6)


(7)

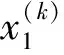

(8)
其中定义π2动力学和x2(t)的误差为
(9)
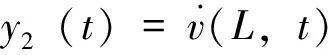
(10)
其中我们定义π02动力学和y2(t)的误差为
(11)
所研究立管系统模型如式(1)描述,为使该系统稳定,本文提出以下控制律
(12)
其中k1,k2,k3,k4,k5,k6>0为控制增益。
注2 边界控制中的信号x1(t)=w(L,t),y1(t)=v(L,t)可由立管顶端的激光位移传感器测得,w′(L,t)和v′(L,t)可由倾角计测得。此控制器设计独立于系统参数,因此对系统参数的变化具有稳定鲁棒性。
若给定Lyapunov函数为
(13)
其中
(14)
其中ζ,λ1,λ2是正的权重常数。
引理4 由式(13)给定的Lyapunov函数具有如下上下界
(15)
其中ϑ1和ϑ2是两个正常数,θ(t)为
(16)
证明 应用不等式(3)和文献[16]中不等式2[v′(x,t)]2≤[w′(x,t)]2可得
(17)
其中μ为正常数。
结合式(14)第一项和式(17)有
(18)
其中
对V2(t)应用不等式(3)可得
(19)
其中
不等式(19)可写为
(20)
结合式(18)和式(20),有
(21)
选取适当的ζ,μ,λ1,λ2,可以得到
(22)
将式(22)代入式(21)可得
(23)
不等式(23)两边加上V3(t),有
(24)
其中ϑ1=min(α1,1)和ϑ2=max(α2,1)是正常数。证毕。
引理5 由式(13)给定的Lyapunov函数对时间的导数具有如下上下界

(25)
其中ϑ>0,ω>0。
证明 将式(13)对时间求导,有
(26)
对V1(t)求导,将式(1)代入,应用分部积分并结合式(3),可得
(27)
其中δ1为任意正常数。
对V2(t)求导,将式(1)代入,应用分部积分并结合不等式(3)-(5),有
(28)
其中δ2,δ3,δ4,δ5为任意正常数。
对V3(t)求导可得
(29)
将式(27)-(29)代入式(26)并结合不等式(3)-(5)可得
(30)
其中δ6~δ18为任意正常数。选择适当参数值ζ,λ1,λ2,k1~k6,δ1~δ18满足如下条件:
由不等式(24)和(30),得出

(31)
3 稳定性分析
定理1 对由式(1)描述的动态系统在边界控制器(12)的作用下,系统具有如下的稳定性
(32)
证明 将式(25)乘以eϑt,有
(33)
对上述不等式积分得
(34)
其中上式表明V(t)是有界的。
类似的,利用不等式(5)和不等式2[v′(x,t)]2≤[w′(x,t)]2并结合(15)和(18),可得
(35)
重排上述两不等式有
(36)
∀(x,t)∈[0,L]×[0,∞)。
从上式我们进一步可得
(37)
∀x∈[0,L],证毕。
4 数值仿真
本节将采用有限差分法来数值仿真研究在内流和海流同时扰动作用下柔性立管的动力学响应,并对所设计控制器(12)的有效性进行验证。柔性立管的系统参数为:L=1 000 m,EI=1.5×107Nm2,EA=4×109Ns/m,T=8.11×107N,mr=350 kg/m,mf=100 kg/m,c1=c2=5 Ns/m2。
海洋洋流速度与深度关系可表示为[2]
(38)
其中V0(t)为洋流表面流速表示为
i=1,2,3,4
(39)

Vi(t)=0.5+0.2cos(0.867t)
(40)
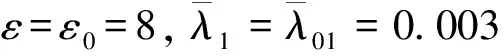
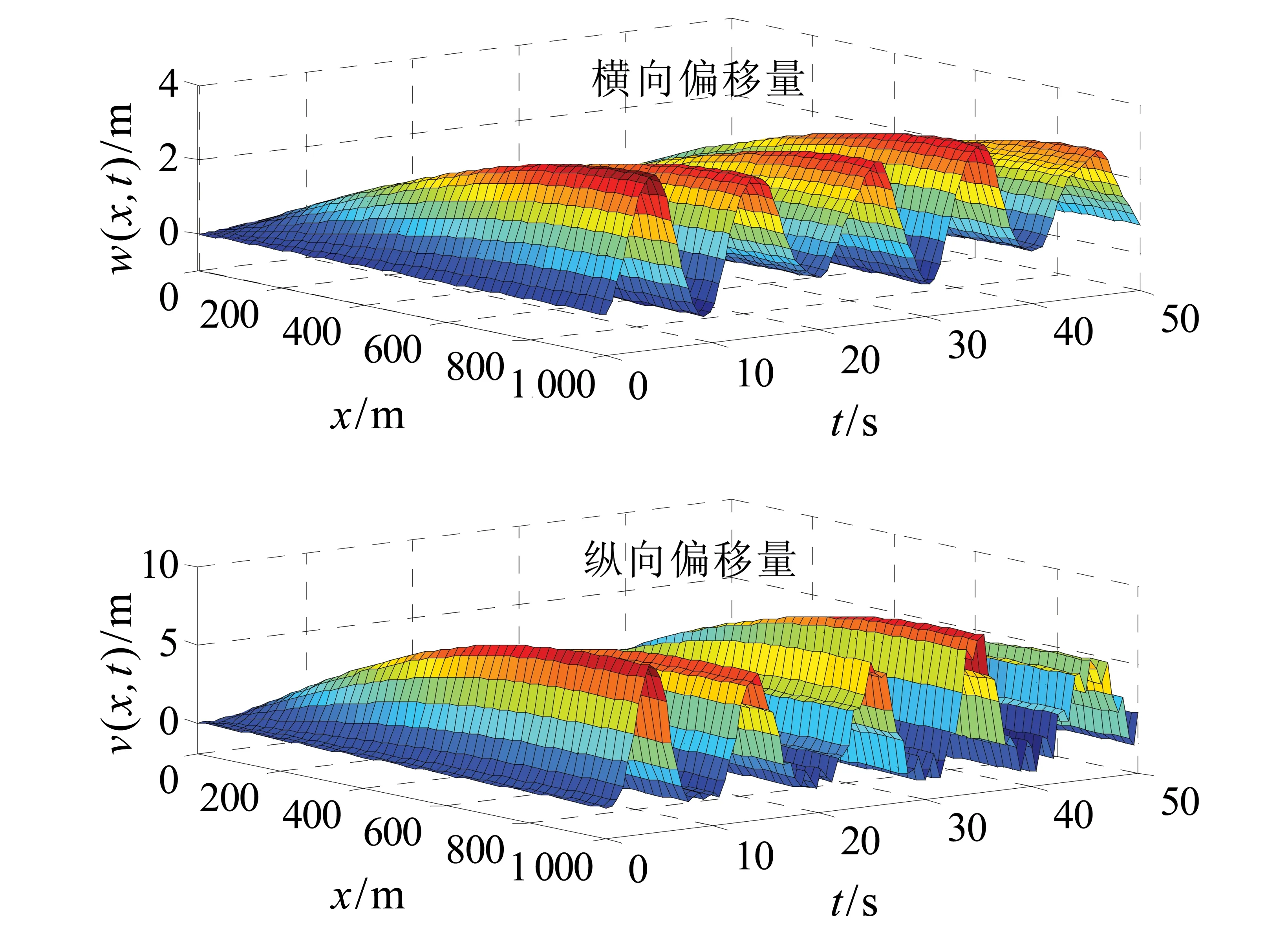
图2 无控制时的立管偏移量图Fig.2 Displacement of the riser without control

图3 控制作用下的立管偏移量Fig.3 Displacement of the riser with control
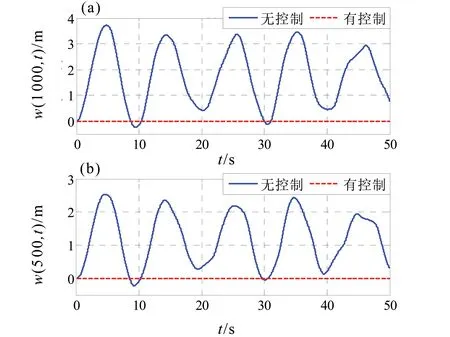
图4 立管横向偏移量:(a) x=1 000 m,(b) x=500 mFig.4 Transverse Displacements of the riser

图5 立管纵向偏移量:(a) x=1 000 m,(b) x=500 mFig.5 Longitudinal displacements of the riser

图6 输出反馈控制输入Fig.6 Output feedback control inputs
图2和图3分别给出了立管在无/有控制作用下三维横、纵向偏移图,图4和图5则分别给出了立管在x=1000 m和x=500 m处无/有控制作用下二维横、纵向振动偏移图。图6给出了二维输出反馈边界控制输入。
由仿真结果图2-图6可得出如下结论:
1)当所提出的输出反馈控制(12)作用于立管系统时,立管的横向振动偏移量和纵向偏移量都数千倍的减小,验证了本文所设计控制器的有效性。
2)在立管的中部(x=500 m),虽然未布置有控制器,但其振动偏移量在控制作用下也有非常显著的减小,体现了边界控制在柔性结构振动抑制中的优势。
3)对比本文图3和文献[1]中的图2(b)和图3(b),可知在控制作用下,本文中立管横、纵向振动偏移量都远远小于文献[1]中控制后立管的横、纵向振动偏移量。因此,本文所提出的输出反馈控制在系统状态获取不精确条件下能更好地抑制立管的二维振动偏移量。
5 结 论
本文研究了海洋柔性立管在时变内流和海流耦合作用下二维振动控制问题。基于其偏微分-常微分方程描述的无穷维模型,采用Lyapunov直接法和高增益观测器技术相结合的综合法,设计了输出反馈边界控制来对立管的二维振动进行控制。其后运用Lyapunov稳定性理论对控制系统的一致最终有界稳定性进行了严格地证明。本文的控制设计及稳定性分析没有任何离散化或者简化系统偏微分方程动力学,因此控制溢出问题将不会产生。最后采用有限差分法来模拟系统的数值解,由仿真结果可知文中所设计二维输出反馈边界控制器的可行性和有效性。
[1] 吴忻生, 李林野, 刘屿, 等. 海洋输油立管的建模及边界控制[J]. 华南理工大学学报(自然科学版), 2012, 40(8): 32-38.
[2] 高红霞, 赵志甲, 吴忻生, 等. 基于内流动力学的海洋输油柔性立管鲁棒边界控制[J]. 控制理论与应用, 2012, 29(6): 785-791.
[3] 邬依林, 刘屿, 吴忻生. 基于时变内流的柔性立管自适应边界控制[J]. 控制理论与应用, 2013, 5(30): 618 -624.
[4] LIU Y, HUANG H W, GAO H X, et al. Modeling and boundary control of a flexible marine riser coupled with internal fluid dynamics [J]. Journal of Control Theory and Applications, 2013, 11(2): 316 -323.
[5] WU H, WANG J, LI H. Design of distributed H∞fuzzy controllers with constraint for nonlinear hyperbolic PDE systems [J]. Automatica, 2012, 48(10): 2535-2543.
[6] GUO B. Riesz basis property and exponential stability of controlled Euler-Bernoulli beam equations with variable coefficients [J]. SIAM Journal on Control and Optimization, 2002, 40(6): 1905-1923.
[7] 翁轩, 杨龙刚, 刘屿, 等. 具有边界扰动柔性机械臂的鲁棒自适应边界控制[J]. 中山大学学报(自然科学版), 2015, 54(3): 44-50.
[8] 邬依林, 刘屿. 分布参数柔性梁的建模与振动边界控制[J]. 中山大学学报(自然科学版), 2013, 52(3): 55-62.
[9] DO K D, PAN J. Boundary control of three-dimensional inextensible marine risers [J]. Journal of Sound and Vibration, 2009, 327(3/4/5): 299-321.
[10] HOWB V E, GE S S, CHOO Y S. Active control of flexible marine risers [J]. Journal of Sound and Vibration, 2009, 320(4-5): 758-776.
[11] HE W, GE S S, HOW B V, et al. Robust adaptive boundary control of a flexible marine riser with vessel dynamics [J]. Automatica, 2011, 47(4): 722-732.
[12] NGUYEN T L, DO K D, PAN J. Boundary control of two-dimensional marine risers with bending couplings [J]. Journal of Sound and Vibration, 2013, 332(16): 3605-3622.
[13] DO K D, PAN J. Boundary control of transverse motion of marine risers with actuator dynamics [J]. Journal of Sound and Vibration, 2008, 318(4/5): 768-791.
[14] GE S S, HE W, HOW B V, et al. Boundary control of a coupled nonlinear flexible marine riser [J]. IEEE Transactions on Control Systems Technology, 2010, 18(5): 1080-1091.
[15] BEHTASH S. Robust output tracking for nonlinear system [J]. International Journal of Control, 1990, 51: 1381-1407.
[16] HE W, ZHANG S, GE S S. Adaptive boundary control of a nonlinear flexible string system [J]. IEEE Transactions on Control Systems Technology, 2014, 22(3): 1088-1093.
Output feedback control for two dimensional vibration of a flexible marine riser
PANChuan1,HOUChang1,WUYilin2
(1. Information and Computer Engineering Institute, Northeast Forestry University, Harbin 150040, China;2. Department of Computer Science, Guangdong University of Education, Guangzhou 510310, China)
The two dimensional vibration control problem of a flexible marine riser with internal fluid dynamics and the ocean current is considered. The dynamic behavior of the flexible riser is described by two partial differential equations and six ordinary differential equations. To improve the vibration control performance and avoid the control spillover, the Lyapunov’s direct method and high-gain observer technique are adopted to develop two output feedback boundary controllers for vibration suppression of the riser system based on its original infinite-dimensional model. With the proposed control, uniform ultimate boundedness under ocean current disturbance and uniform boundedness of the closed-loop state are proved. The simulation results have verified the effectiveness of the designed boundary control scheme.
marine risers; two dimensional vibration; boundary control; output feedback control; Lyapunov’s direct method
10.13471/j.cnki.acta.snus.2016.04.004
2016-04-13
广东省科技计划资助项目(2016A010106007);广东第二师范学院教授博士科研专项经费资助项目(2014ARF25)
盘川(1995年生),女;研究方向:分布参数系统;通讯作者:侯畅;E-mail:zzuhchang@163.com
TP24
A
0529-6579(2016)04-0018-08
