基于奇异值分解的惯性测量组合减振系统非线性刚度识别

张鹏飞，苏华昌，吴家驹



基于奇异值分解的惯性测量组合减振系统非线性刚度识别

张鹏飞，苏华昌，吴家驹

（北京强度环境研究所，北京，100076）

介绍了基于奇异值分解的复解析小波脊线提取方法，并用仿真算例进行了验证。设计了基于冲击响应的非线性刚度识别程序。采用半正弦冲击对惯组减振系统的非线性特性进行试验研究，验证了方法的可行性，分析了非线性系统刚度和阻尼的变化规律。对于非线性特征比较明显的结构，使用该方法的参数识别结果具有较高精度。

非线性刚度；小波变换；奇异值分解；小波脊线

0 引 言

结构动力学分析与试验相关性研究的目的是通过试验结果修改数学模型，然后用修正后的数学模型计算复杂振动载荷下的响应，这对于线性系统来说困难不大。然而，火箭和航天器实际上呈现出某种程度的非线性品质[1]。非线性可能是由结构（端头快速连接）、几何（飞船的支撑机构）和材料性质（阻尼减振器）等因素造成的。虽然业内已有许多非线性系统的结构动力学分析软件，但是大多数都需要知道特征化的非线性特征。因此，通过试验识别结构非线性特征是一个亟待解决的问题。

惯性测量组合（惯组）是测量导弹运动姿态的装置。为了提高惯组在振动环境中的适应性，经常将惯性敏感器件通过橡胶减振器连接到载体上[2]。惯组小系统频响特性测量结果表明，这个弹性环节呈现出很强的非线性。图1为实测的惯组角振动传递率随频率的变化曲线，其传递率特征随激励量级的变化很大，系统的增益和谐振频率随激励量级下降，这表明系统呈现出含有渐软刚度的非线性特征。

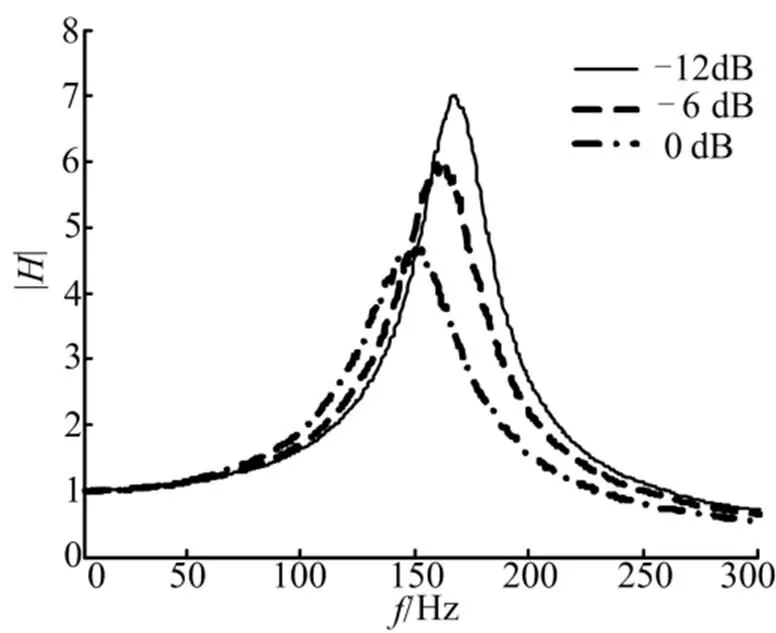
图1 惯组减振系统角振动传递率

目前，对于减振器非线性刚度的识别，多是基于静刚度或正弦定频试验的刚度曲线，使用最小二乘原理进行拟合[3,4]。然而减振器使用环境多数存在冲击载荷，在更接近真实使用环境下对非线性参数的识别结果更加适用。本文基于非线性减振系统的冲击响应，给出了基于复解析小波和奇异值分解的非线性刚度识别方法，识别出刚度-载荷曲线，并用含橡胶减振器的惯组试验数据进行了验证，结论对于惯组减振器系统非线性参数识别和建模具有一定的参考价值。

1 基于奇异值分解的复解析小波脊线提取法

非线性系统的冲击响应具有非平稳信号特征。小波脊线能较好地揭示信号瞬时频率的变化情况。复解析小波变换将小波变换和Hilbert变换紧密结合在一起，具有一定的自适应分析能力。通过复函数连续小波变换得到小波尺度谱后，使用奇异值分解（Singular Value Decomposition，SVD）方法降噪，然后通过求小波系数的模极大值点来提取小波脊线[5~7]。该方法更加适用于试验获得的低信噪比信号的小波脊线提取。

复解析小波函数具有如下的表达形式：

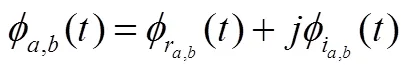
（3）

式中

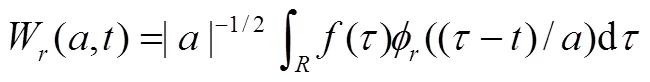
（5）

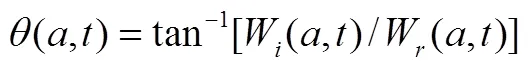
（7）

由小波变换的定义可知，小波变换相当于一系列带通滤波器对信号进行多带通滤波，带通滤波器的中心频率和带宽与尺度成反比，且带宽随中心频率的变化自动调节，体现了对信号的自适应分析能力。复解析小波变换实现了信号带通滤波和Hilbert变换的统一，自适应地提取信号的包络等特征。

小波尺度谱可定义为

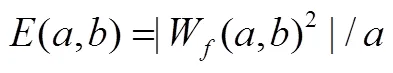
在某一时刻小波系数的最大值满足

（9）

当取不同的值，所有的最大值点的集合形成了小波脊线。理论上可以通过直接求出时频面上每一时刻小波系数的模极大值来获得信号中各分量对应的小波脊线，这是最简单的一种脊线提取方法，但极易受到噪声干扰，因此不适合工程应用。

SVD是一种常用的时频滤波方法，可用于消除信号中的随机噪声成份，提取信号中的周期成份[9]，本文选取该方法对小波尺度谱进行降噪。设矩阵表示信号的小波尺度谱，在奇异值理论中，秩为的×阶矩阵的奇异值分解可表示为

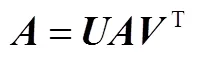
式中和分别是×阶和×阶正交矩阵，=diag（σ1，σ2，…，σ，0，0，…，0）是×阶对角矩阵，其对角元素为的奇异值，并按降序排列。根据Frobeious范数意义下矩阵最佳逼近定理，信号在小波域中有用的信号主要由前个较大的奇异值反映，噪声信号由后面较小的奇异值反映，去掉代表噪声信号的较小奇异值，则源信号中的噪声被去除。为了确定有用的奇异值，首先定义奇异值σ所占能量比重为

（11）

然后，给定一个阈值，将满足r<(=1，…，)的奇异值置零，再进行奇异值分解的逆运算，最终得到矩阵，那么矩阵就是矩阵的秩为的最佳逼近矩阵，就是降噪后的小波尺度谱。

对小波尺度谱进行SVD滤波后，就可以通过选取各个时刻小波系数模极大值点对应的尺度来提取小波脊线。

2 仿真算例

为了验证复解析小波及其脊线提取方法在非平稳信号处理中的先进性，取仿真信号进行试验。仿真信号由下式给出：

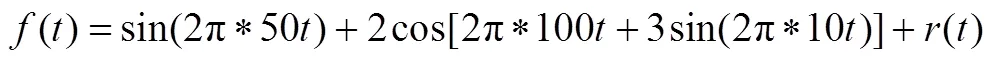
式中()是方差为1的白噪声，[0，1]。

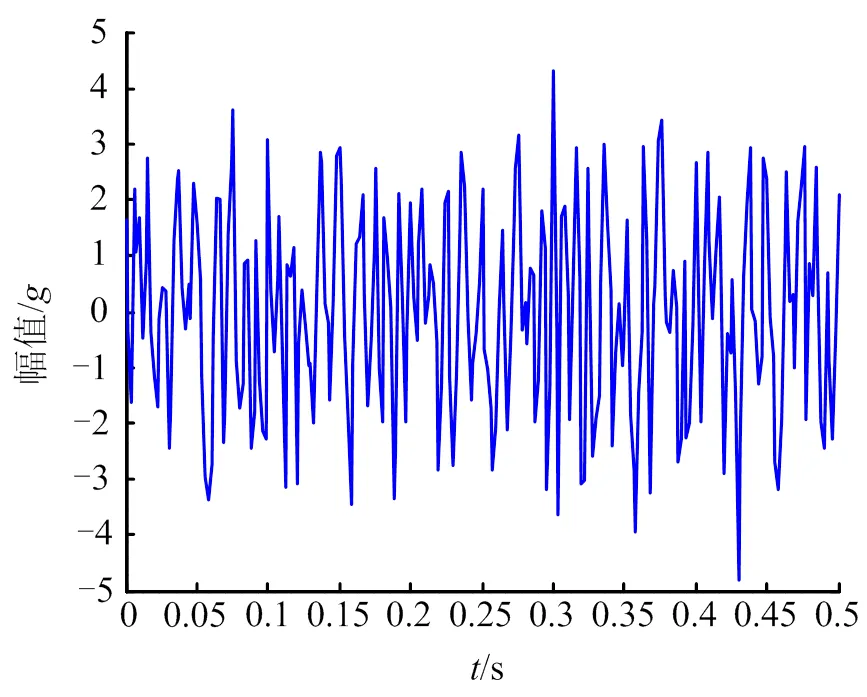
图2 信号f(t)的时域波形

a）直接模极大值法

b）基于SVD的复解析小波模极大值法

图3 不同方法所得()小波脊线的对比

3 非线性刚度识别

3.1 非线性系统的数学模型

根据图1中所表现出来的惯组减振器系统的非线性特征，本文对减振器采用立方刚度模型表征。这种情况下，力-位移关系具有以下形式[10]：

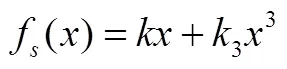
（14）

式中为质量；为阻尼系数。

3.2 非线性刚度识别程序设计

对于式（14），采用谐波平衡法求解，可以得到频率和振动幅值间存在如下的关系：

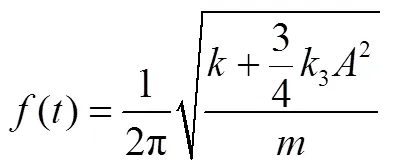
根据式（15），当已知质量时，根据自由衰减信号的小波脊线提取的频率和幅值信息，采用最小二乘原理可以识别出和。对于粘性阻尼，自由衰减信号存在指数形式的包络曲线：

（16）

非线性刚度的识别程序可以汇总为：

a）用敲击法或基础激励法测得系统的加速度自由衰减时间历程；

b）用数字积分获得位移自由衰减时间历程；

c）连续复解析小波变换；

d）SVD滤波降噪；

e）取小波系数模极大值得到脊线；

f）从脊线计算瞬时频率的包络；

g）由衰减包络拟合得到的曲线识别出非线性参数值。

4 实际信号分析

用包含橡胶减振器的惯组来检验上述方法。惯组通过橡胶减振器连接在振动平面上，电动振动台对振动平台施加半正弦冲击激励。振动控制点在振动平面上，惯组上安装加速度传感器测量减振后信号，试验原理如图4所示。图5为实测的惯组减振后加速度自由衰减时间历程。

在Matlab软件中使用数字积分法对加速度信号进行积分，获得位移的自由衰减时间历程。初始速度和初始位移的影响可通过离散小波变换消除积分结果中的直流分量和趋势项来消除。对位移信号进行连续小波变换得到小波尺度谱，并选取每个时刻下小波系数模的最大值，得到如图6所示的小波尺度谱的等高线和脊线。

图4 惯组基础激励试验原理

图5 自由衰减时间历程

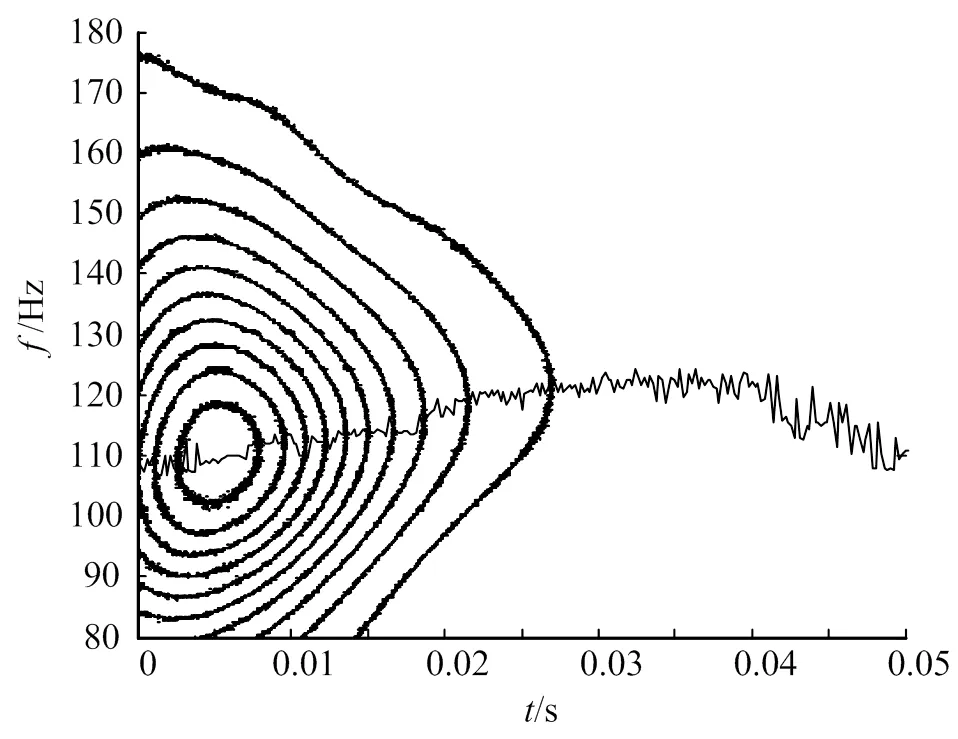
图6 小波尺度谱的等高线和脊线

由于信号噪声较大，提取到的脊线不光滑。通过SVD法对时频谱进行降噪，阈值取0.02，降噪后的小波尺度谱等高线和脊线如图7所示。SVD降噪后脊线光滑，准确反映了瞬时频率随时间的变化。

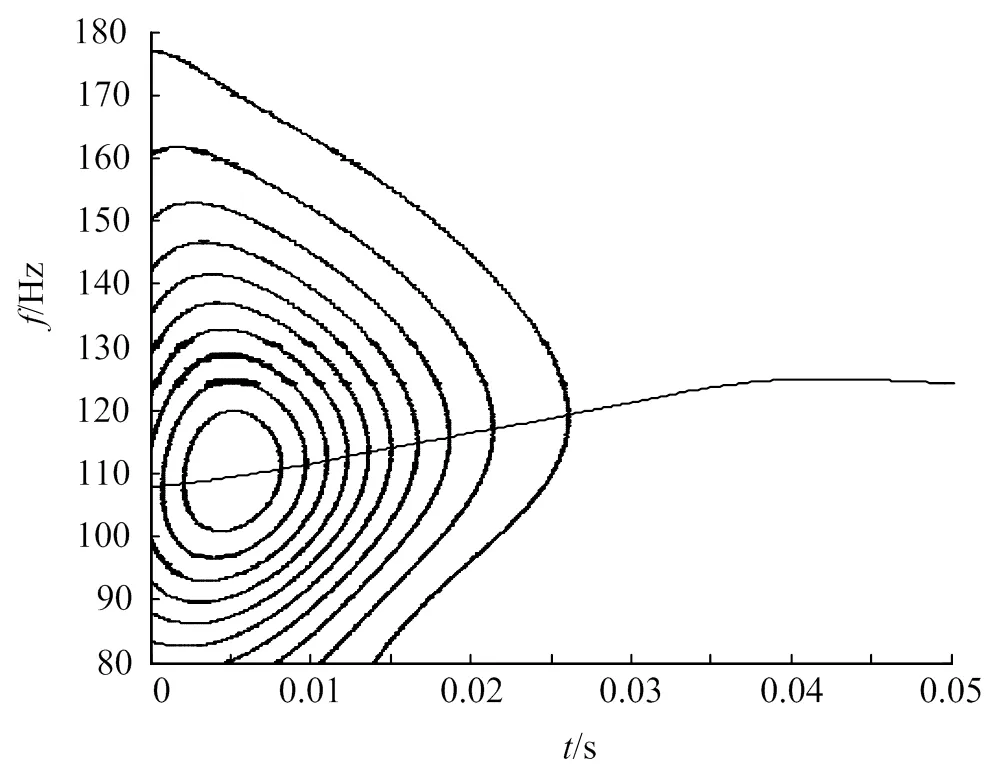
图7 SVD降噪后的小波尺度谱等高线和脊线

对位移自由衰减信号进行Hilbert变换后获得其幅值包络曲线，结合小波脊线得到瞬时频率随振动幅值变化的曲线，如图8所示。取固定时间间隔为0.1 s，随着的平移，计算出结构粘性阻尼随时间的变化函数，进而得到阻尼比关于振动幅值的函数，如图9所示。

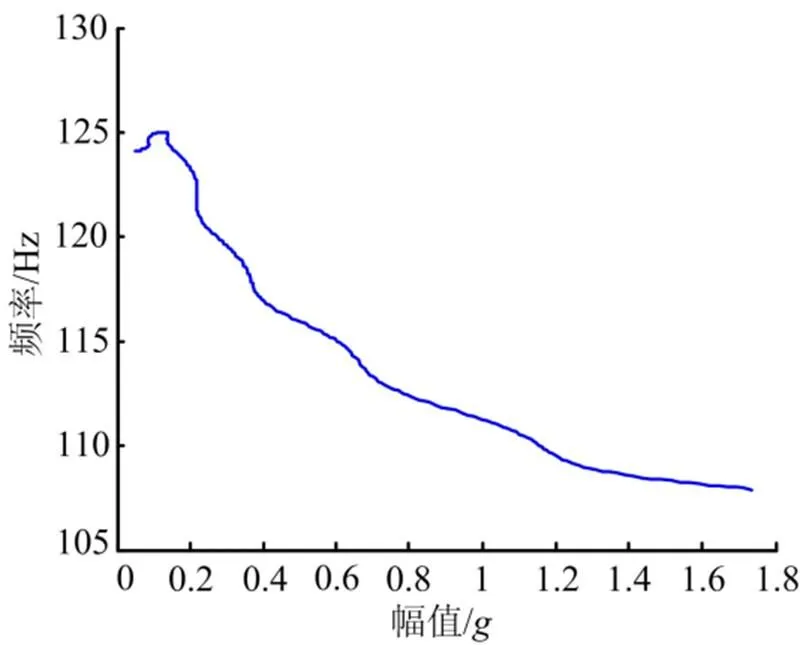
图8 瞬时频率随振动幅值的变化

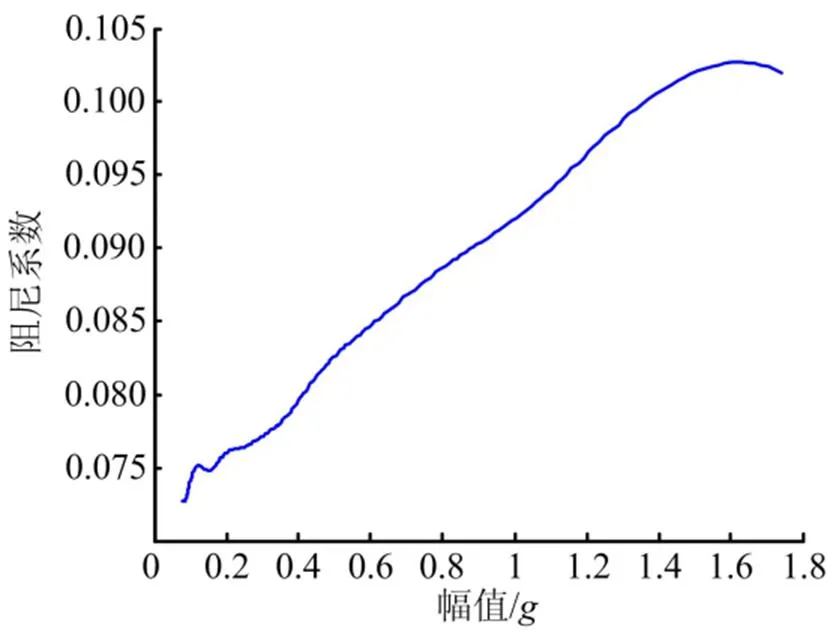
图9 阻尼系数随振动幅值的变化

根据式（15），进一步得到如下关系：

式中为采样点数。

将图8中的频率和幅值代入式（17），得到最小二乘意义下的刚度和。从该组试验数据识别出惯组减振系统的线性刚度=5.66×106N/m，立方刚度=-1.68×1013N/m3。

试验的识别结果表明橡胶减振器符合渐软系统的非线性特征：随加载量级加大刚度变小，阻尼增大。根据冲击响应识别出的非线性刚度特征与文献[3]中使用定频激励法的结果规律一致。根据识别出的频率和阻尼特性，可以拟合出结构的非线性频响函数随不同加载量级的分布，如图10所示。从图10可以看出，随着加载量级的增加，结构的共振频率降低，共振幅值降低，这与图1中的试验结果规律一致。为了验证参数识别的精度，将上述识别出的非线性刚度参数代入式（14）中，使用4阶Runge-Kutta法得到相同激励下的响应曲线，并与实测曲线进行对比，如图11所示。从图11中可见，实测曲线与计算曲线符合很好，说明识别出的和具有较高精度。

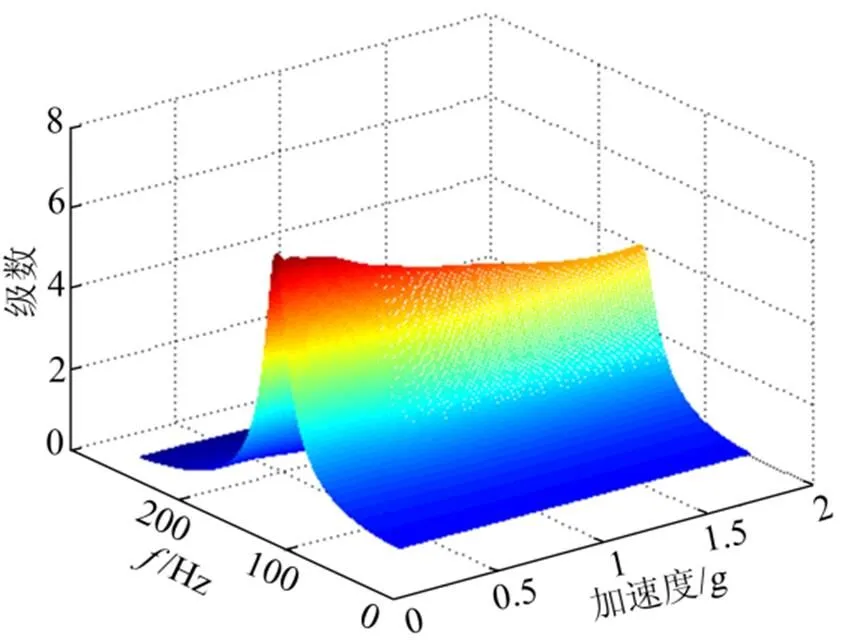
图10 拟合后的非线性频响函数

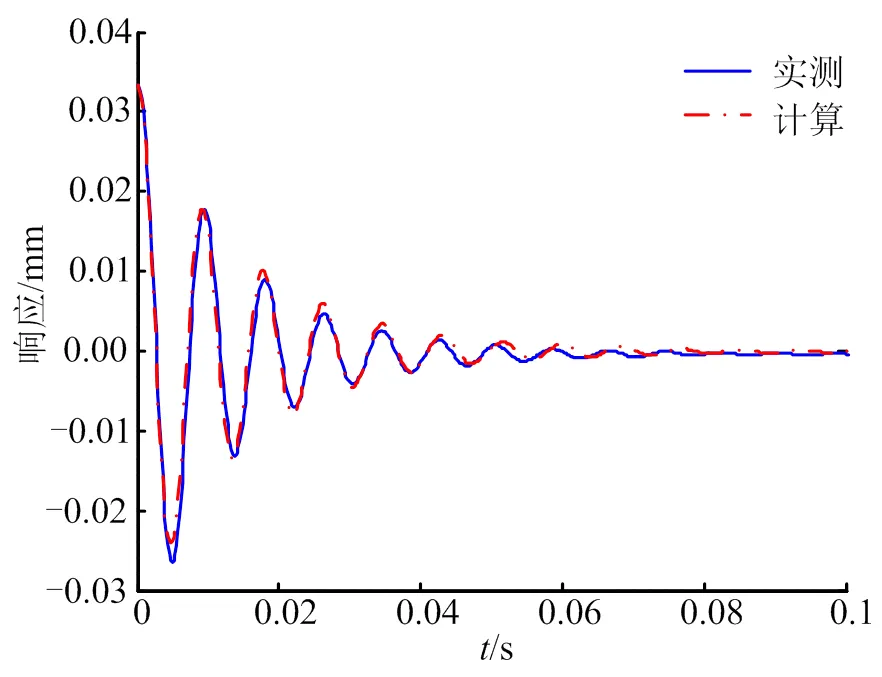
图11 实测与计算结果对比

5 结 论

本文在电动振动台上模拟冲击使用环境，对惯组减振系统的非线性特性进行研究，主要得到以下结论：

a）利用基于SVD的复解析小波脊线提取方法，准确地得到减振后自由衰减信号的时频分布。试验表明SVD法能有效降低噪声的影响，有利于准确提取小波脊线，进而得到惯组减振系统的频率-幅值曲线。

b）根据惯组减振系统的传递特性试验数据所表现的特点，建立了软特性三次刚度动力学模型。考虑到减振器的使用环境多数存在冲击载荷，设计了基于冲击响应的非线性刚度识别程序。

c）使用惯组减振系统半正弦冲击试验的自由衰减数据进行非线性参数识别，验证了模型和识别方法的有效性。分别在频域和时域对参数识别结果与试验进行对比，表明非线性刚度识别具有较高的精度。研究结果对于惯组减振器系统非线性参数识别和建模具有一定的参考价值。

[1] 李欣业, 陈予恕, 张琪昌. 火箭非线性动力学行为研究中的若干问题[J]. 河北工业大学学报, 2001, 30(6): 74-78.

[2] 姚建军. 捷联惯导系统不同隔振模式的比较[J]. 强度与环境, 2009, 36(2): 19-27.

[3] 樊文欣, 杨桂通, 赵俊生, 李双虎. 金属橡胶减振器非线性建模及仿真研究[J]. 车用发动机, 2009(5): 53-56.

[4] 韩德宝, 宋希庚, 薛冬新. 橡胶减振器非线性动态特性的试验研究[J]. 振动工程学报, 2008, 12(1): 102-106.

[5] Staszewski W J. Identification of non-linear systems using multi-scale ridges and skeletons of the wavelet transform[J]. Journal of Sound and Vibration, 1998, 214(4): 639-658.

[6] 吴宏钢, 秦毅, 秦树人. 基于重分配配算法和奇异值分解的多小波脊线提取[J]. 振动与冲击, 2009, 28(12): 9-14.

[7] Brenner M. Nonstationary dynamics data analysis with wavelet-SVD filtering[R]. AIAA-2001-1586, 2001.

[8] 张家凡, 易启伟, 李季. 复解析小波变换与振动信号包络调解分析[J]. 振动与冲击, 2010, 29(9): 93-96.

[9] 钱征文, 程礼, 李应红. 利用奇异值分解的信号降噪方法[J]. 振动、诊断与测试, 2011, 31(4): 459-463.

[10] 陈前, 高雪. 结构动力学中的非线性问题[M]. 北京: 机械工业出版社, 2012.

Identification of Nonlinear Stiffness of Inertial Measurement Unit with Vibration Absorber System Based on Singular Value Decomposition

Zhang Peng-fei, Su Hua-chang, Wu Jia-ju

(Beijing Institute of Structure and Environmen Engineering, Beijing, 100076)

Wavelet ridge extracting method based on singular value decomposition(SVD) was introduced. A numerical example was actualized to validate the method. Programs of identifying nonlinear stiffness based on impulse response were designed. The experiment of inertial measurement unit with rubber vibration absorber under the load of half sine pulse was conducted to validate the feasibility of the method. The changing regularities of nonlinear stiffness and damp were analysed. Using this method, the parameter identified results are high precise to nonlinear system.

Nonlinear stiffness; Wavelet transformation; Singular value decomposition; Wavelet ridge curve

1004-7182(2016)03-0068-05

10.7654/j.issn.1004-7182.20160316

V214

A

2015-06-10；

2015-08-03

张鹏飞（1986-），男，工程师，主要研究方向为结构动力学