大口径天线微波短脉冲辐射特性的数值分析

邢笑月，黄文华，刘小龙，汪海波

(西北核技术研究所，西安　710024；高功率微波技术重点实验室，西安　710024)



大口径天线微波短脉冲辐射特性的数值分析

邢笑月，黄文华，刘小龙，汪海波

(西北核技术研究所，西安710024；高功率微波技术重点实验室，西安710024)

摘要：为使大口径天线能够正常辐射几十纳秒甚至几纳秒的微波脉冲，通过数值计算，获得了大口径天线主轴方向不同距离及偏离主轴不同角度处，辐射场波形脉冲宽度及电场强度幅值随微波激励脉冲宽度的变化关系；同时，还获得了不同口径尺寸天线辐射场波形脉冲宽度及电场强度幅值随偏离主轴不同角度的变化关系。结果表明：在口径天线远场条件下，天线主轴方向的辐射场波形无畸变；偏离主轴，辐射场波形会出现不同程度的脉冲展宽及幅值减小等波形畸变现象，偏离主轴角度越大，激励脉冲宽度越小，畸变越严重；在10 dB波束宽度范围内，不同尺寸口径天线的辐射场波形不变。

关键词：大口径天线；微波短脉冲；微波激励脉冲宽度；辐射场波形

天线性能指标通常是在连续波或脉冲宽度为微秒量级以上的宽脉冲条件下测试获得，对脉冲宽度为几十纳秒、甚至几纳秒的短脉冲，天线性能测试系统尚不成熟，天线用于短脉冲信号发射时的辐射性能参数，只能参考宽脉冲条件下的测试结果。然而，随着天线口径的增大，纳秒级短脉冲特性对天线辐射场波形的影响将不能忽略[1]。因此，开展大口径天线的短脉冲微波辐射特性研究，获取短脉冲激励大口径天线时辐射场波形的变化规律，对开展大口径天线的设计、性能指标的准确测量及大口径天线的短脉冲辐射场测量，都具有指导意义。

调研国内外相关研究可知，1989年Baum等对阶跃脉冲激励下口径的辐射特征进行了初步分析[2-3]，首次给出了脉冲口径天线辐射场的时域积分表达式，建立了脉冲口径天线分析的理论基础。刘小龙等对Baum的分析方法进行了改进[4-5]，在拉氏域计算中，对相位不进行近似，只在幅度上对距离进行近似。通过解析积分运算，获得了阶跃脉冲激励口径天线的瞬态辐射场解析表达式。本文在此基础上，采用数值方法，计算获得了不同口径天线主轴方向不同距离处及偏离主轴不同角度下的辐射场波形随微波激励脉冲宽度的变化规律，明确了天线尺寸对微波激励脉冲宽度的要求。

1理论表达式

任一形状的口径天线及坐标如图1所示。

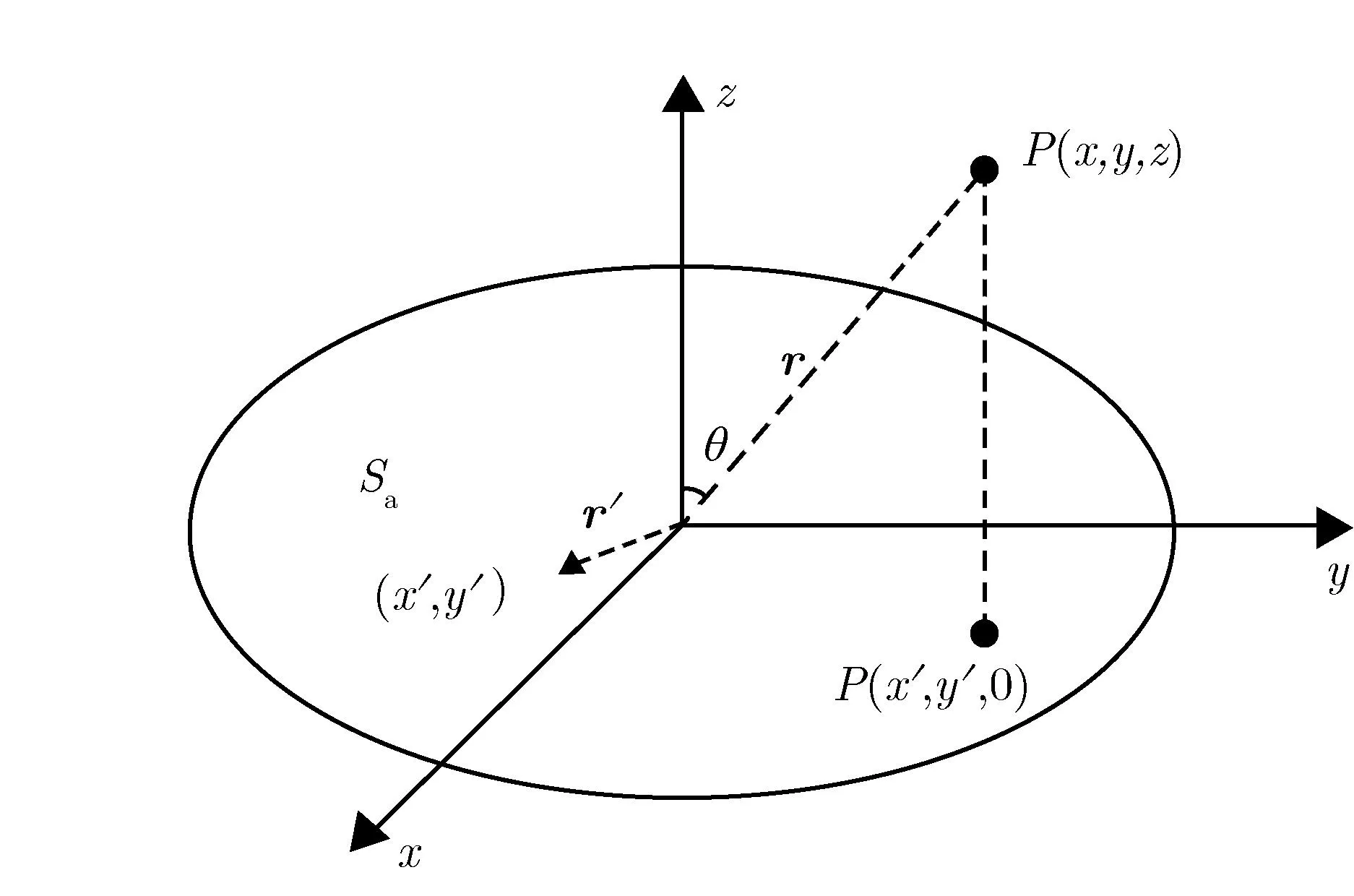
图1　口径天线形状及坐标Fig.1　Aperture shape and its coordinate of an antenna

图1中，口径面Sa位于z=0平面上，令源点坐标为(x′,y′,z′)，其中，z′=0。口径上的电场切向分量为

(1)

其中，ex、ey为x、y方向的单位矢量。经拉氏变换后，空间点P的电场强度为

(2)

其中，R为源点到空间点P的距离；r表示口径中心到空间点P的位移矢量；r′表示口径中心到源点的位移矢量；γ为空间传播常数，γ=s/c，c为光速。

假设口径上切向电场同时到达且均匀分布，电场沿x轴方向，并假设口径上场的峰值功率为1/η，η为自由空间波阻抗，忽略口径边缘的电流不连续性对辐射的影响，口径外电场为零，因此，式(1)变为

(3)

其中，激励源f(t)为上升时间百皮秒量级、脉冲宽度纳秒量级的典型微波短脉冲[6]。

将式(3)代入式(2)中，经拉氏反变换，并分解为两个标量表达式

Ex(r,t)=

(4)

Ez(r,t)=

(5)

令t=τ+R/c进行变量替换，并对式(4)进行离散化。其中，τ=n·Δt，x′=i·Δx，y′=i·Δy，Δt为时间步长。这样，口径面上每一空间面元及每一离散时刻的切向场可以叠加到其有贡献的离散时刻的辐射场上，从而得到辐射场的离散波形。

2数值计算及结果分析

典型微波短脉冲波形如图2所示。电场幅值E0为1 V·m-1，脉冲宽度为1 ns，上升、下降沿时间均为0.3 ns，载波9.7 GHz。利用式(4)进行数值计算，考察在主轴不同距离处辐射场波形的变化规律。

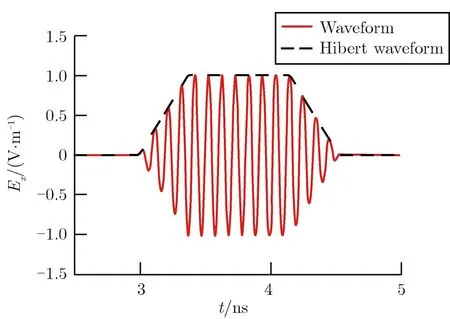
图2　典型微波短脉冲激励电场波形Fig.2　The E-field excitation waveform of a typical microwave pulse

2.1主轴方向不同距离处的辐射场波形

以直径D=6 m的圆形口径为例，改变微波激励脉冲宽度，计算辐射场主轴方向不同距离处波形的脉冲宽度和电场强度幅值变化率，结果如图3和图4所示。其中，天线辐射远场区域分界距离为rD=2D2/λ。

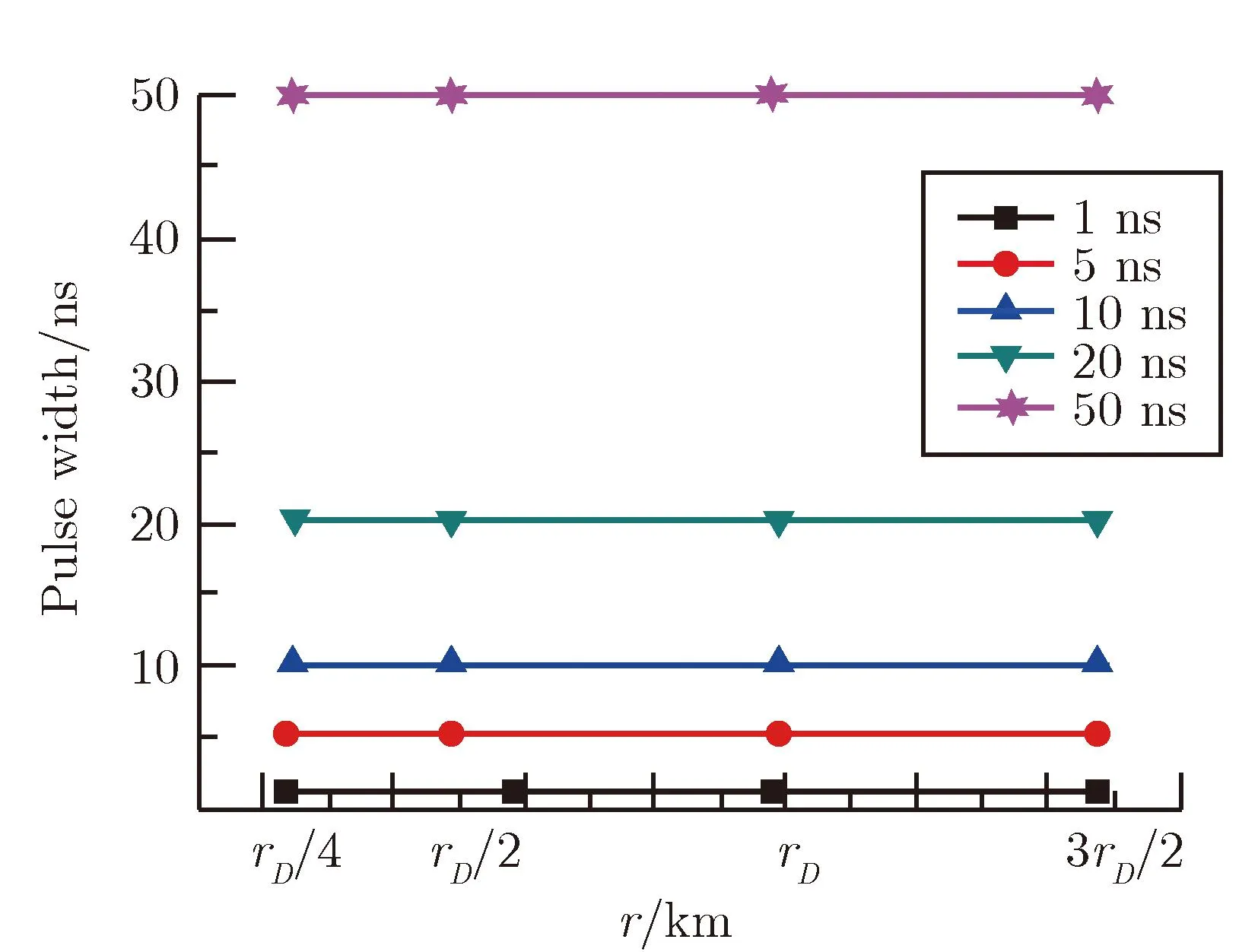
图3　主轴方向不同距离处辐射场波形的脉冲宽度Fig.3　Pulse width of radiation field waveform at the different positions on the principal axis

从图3可以看出，在微波激励脉冲宽度分别为1,5,10,20,50 ns等5种情况下，辐射场主轴方向不同距离处辐射场波形的脉冲宽度一致，不随主轴方向不同距离而变化。

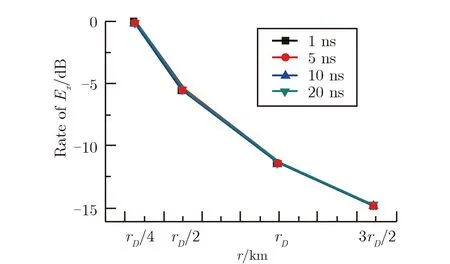
图4　主轴方向不同距离处的电场强度幅值变化率Fig.4　Rate of amplitude of electric field strengthat the different positions on the principal axis

从图4可以看出，在微波激励脉冲宽度分别为 1，5，10，20 ns等4种情况下，辐射场波形的电场强度幅值变化率随距离的变化规律一致，不随微波激励脉冲宽度的改变而变化。

上述数值计算结果表明，在口径天线1/4远场条件范围以外，改变微波激励脉冲宽度，对口径天线主轴上的辐射场波形影响不大。

2.2偏离主轴角度对辐射场波形的影响

以直径D=6 m的圆形口径为例，在不同的微波激励脉冲宽度下，计算口径天线偏离主轴不同角度处的辐射场波形脉冲宽度及电场强度幅值变化率，结果如图5和图6所示。

图5　辐射场波形脉冲宽度变化率随偏离天线主轴角度的变化Fig.5　Rate of pulse width of radiation field waveform changing with angles deviated from the principal axis

从图5可以看出，5种微波激励脉冲宽度下，辐射场波形脉冲宽度变化率随偏离天线主轴角度而变化。当微波激励脉冲宽度≥5 ns且θ在口径天线10 dB波束宽度范围内时，辐射场波形脉冲宽度的变化率最大不超过6%；但当微波激励脉冲宽度≤5 ns时，远场辐射场接收波形的脉冲宽度变化率随偏离主轴角度θ的增大而明显增大。当微波激励脉冲宽度缩小至1 ns且θ=3°时，辐射场波形脉冲宽度的变化率增大到80%，辐射场波形发生严重脉宽展宽现象。

图6　辐射场电场强度幅值变化率随偏离天线主轴角度的变化Fig.6　Rate of amplitude of electric field strengthchanging with angles deviated from the principal axis

从图6可以看出，5种微波激励脉冲宽度下，辐射场电场强度幅值变化率随偏离天线主轴角度而变化。当微波激励脉冲宽度≥5 ns，且θ在口径天线10 dB波束宽度范围内时，辐射场的电场强度幅值变化率不随微波激励脉冲宽度改变而变化；但当微波激励脉冲宽度缩小至1 ns时，远场辐射场接收波形的电场强度幅值变化率随偏离主轴角度θ的增大而显著变化，当θ=3°时，电场强度幅值与微波激励脉冲宽度5 ns以上的辐射场波形电场强度幅值相比，减小约20 dB，变化十分明显。

选定偏离主轴角度为口径天线辐射场10 dB波束宽度范围，计算直径D为6 m的口径天线辐射场波形的脉冲宽度变化率随微波激励脉冲宽度的变化情况，结果如图7所示。

从图7可以看出，当微波激励脉冲宽度≥10 ns时，口径天线10 dB波束宽度范围内的辐射场波形脉宽变化率在5%以下；当微波激励脉冲宽度缩小至1 ns时，D=6 m口径天线的辐射场波形脉冲宽度变化率增大至20%。

以上数值计算结果表明，改变微波激励脉冲宽度，口径天线偏离主轴不同角度处辐射场波形会出现不同程度的脉冲展宽等畸变现象；当微波激励脉冲宽度缩小至1 ns时，辐射场波形的展宽现象非常明显。

图7　10 dB波束范围内辐射场波形脉冲宽度变化率随微波激励脉冲宽度的变化Fig.7　Rate of pulse width of radiation field waveform changing with microwave excitation pulse width in the domain of 10 dB beamwidth

2.3口径尺寸对辐射场波形的影响

保持微波激励脉冲宽度为50 ns不变，计算分析不同尺寸圆形口径天线偏离主轴不同角度处的辐射场波形的变化，结果如图8和图9所示。其中，天线辐射远场区域分界距离为rD=2D2/λ。

图8　偏离主轴不同角度处辐射场波形脉冲宽度变化率与口径尺寸的关系Fig.8　Rate of pulse width of radiation fieldwaveform changing with the aperture size

从图8可以看出，在口径天线辐射场不同角度下，辐射场波形的脉冲宽度变化率在3%以下。

图9　偏离主轴不同角度处电场强度幅值变化率与口径尺寸的关系Fig.9　Rate of amplitude of electric field strength changing with the aperture size

从图9可以看出，在口径天线辐射场不同角度下，辐射场的电场强度幅值变化率基本一致，在0.2 dB以下。这说明脉冲宽度50 ns的微波激励脉冲对直径为6 m以下的口径天线，不会造成天线辐射场波形脉宽展宽和幅值减小等波形畸变现象。

3结论

在分析口径场瞬态辐射特性的基础上，通过解析积分运算，采用数值方法计算获得了大口径天线主轴方向不同距离及偏离主轴不同角度处，辐射场波形脉冲宽度、电场强度幅值与微波激励脉冲宽度的变化关系。计算结果表明：在口径天线远场条件下，天线主轴方向的辐射场波形无畸变；偏离主轴不同角度处，辐射场波形会出现不同程度的脉冲展宽、幅值减小等波形畸变现象；脉冲宽度为50 ns的微波激励脉冲对直径为6 m以下的口径天线，不会造成天线辐射场波形脉宽展宽和幅值减小等波形畸变现象。

参考文献

[1]BENFORD J, SWEGLE J A, SCHAMILOGLU E, et al. High Power Microwaves[M]. 北京: 国防工业出版社, 2009.(BENFORD J, SWEGLE J A, SCHAMILOGLU E, et al. High Power Microwaves[M]. Beijing: National Defense Industry Press, 2009.)

[2]BAUM C E. Radiation of impulse-like transient field[R]. Sensor and Simulation Note, 1989.

[3]傅君眉, 冯恩信. 高等电磁理论[M]. 西安: 西安交通大学出版社, 2000: 259-262.(FU Jun-mei, FENG En-xin. Advanced Electromagnetic Theory[M]. Xi’an: Xi’an Jiaotong University Press, 2000: 259-262.)

[4]刘小龙, 王向晖, 蒋延生, 等. 口径天线辐射脉冲持续时间的研究[J]. 微波学报, 2004, 20(3): 30-32.(LIU Xiao-long, WANG Xiang-hui, JIANG Yan-sheng, et al. Research on the radiation pulse width of the aperture antenna[J]. Journal of Microwaves, 2004, 20(3): 30-32.)

[5]刘小龙, 王向晖, 汪文秉, 等. 单极性亚纳秒脉冲激励口径的辐射特性[J]. 强激光与粒子束, 2003, 15(11): 1 103-1 106.(LIU Xiao-long, WANG Xiang-hui, WANG Wen-bing, et al. Radiant characteristics of subnanosecond and monopolar pulse-excited aperture[J]. High Power Laser and Particle Beams, 2003, 15(11): 1 103-1 106.)

[6]曹磊, 张昕, 李磊. E面扇形喇叭天线对电磁脉冲响应特性的分析[J]. 应用科技, 2012, 39(1): 21-25.(CAO Lei, ZHANG Xin, LI Lei. Response characteristics of E-plane sectorial horn antenna excited by electromagnetic pulses[J]. Applied Science and Technology, 2012, 39(1): 21-25.)

Numerical Studies on Radiation Characteristics of Large-Aperture Antennas Excited by Short Microwave Pulses

XING Xiao-yue,HUANG Wen-hua,LIU Xiao-long,WANG Hai-bo

(Northwest Institute of Nuclear Technology,Xi’an710024，China；Science and Technology on High Power Microwave Laboratory，Xi’an710024，China)

Abstract:In order to meet the needs for large aperture antennas to normally radiate dozens of nanoseconds or even a few nanoseconds microwave pulses, we calculated the relations between pulse width and amplitude of the radiation field at different positions on the principal axis for different angles deviated from the principal axis, and obtained the relations between pulse width and amplitude of the radiation field, and exciting microwave pulse width for different aperture sizes. The results indicates that the distances on the principal axis has no significant influence on the antenna radiation field waveform; the antenna radiation field waveforms would exhibite pulse widening and amplitude decreasing for larger deviation angle; in the domain of 10 dB beamwidth, the antenna radiation field waveform remains unchanged for different aperture sizes.

Key words:large-aperture antenna;short microwave pulses;microwave excitation pulse width;radiation waveform

文献标志码：A

文章编号：2095-6223(2016)010504(5)

中图分类号：O0441.4

作者简介：邢笑月(1986- )，女，陕西西安人，工程师，硕士，主要从事高功率微波技术研究。E-mail:xingxiaoyue@nint.ac.cn

收稿日期：2015-08-19；修回日期：2015-12-23