新媒体技术因子对高等教育影响分析

侯冬青　尹君（.郑州大学西亚斯国际学院新闻与传播学院，河南　郑州　4550；.河南省科学技术信息研究院，河南　郑州　450003）



新媒体技术因子对高等教育影响分析

侯冬青1尹君2
（1.郑州大学西亚斯国际学院新闻与传播学院，河南郑州451150；2.河南省科学技术信息研究院，河南郑州450003）

［摘要］新媒体技术已对整个高校教学系统中教学结构、教学模式及教学手段等带来重大变革，那么新媒体技术到底对高校教育产生了多大的影响，这些影响反应在我们的现实生活当中又是什么样，本文简略对其相互影响进行了探讨。

［关键词］新媒体技术；网络环境；教育；因子

1　背景

1.1研究项目概况

近年来，新媒体技术在各个高校间得到了广泛的普及和应用，为了得到确切的新媒体技术对现有高校影响的成分分析报告，我们在全国范围内选取了4个城市，在每个城市采用街头随机访问的方式对关注高校的人群进行调查，随机选择10所高校样品中的一所，并给出新媒体技术对其影响的评价（9分制）。

访谈城市：上海、北京、广州和郑州。

抽样高校：上海交大、复旦大学、北京大学、北京师范大学、华中科技大学、武汉大学、暨南大学、华南理工大学、郑州大学、河南大学。

分析目的：第一，在这10所高校中采用新媒体技术最广泛的是哪一所；第二，人们的选择倾向在这4个城市之间有无差异。

预期目标：第一，河南两所高校同另外8所高校的在新媒体技术应用上的差异；第二，如果能从中选出新媒体技术应用最好的一所，则最为理想。

由于本课题一些其他研究目的的限制，研究时无法采用每位受访者对高校间新媒体技术每个城市中大约收集30～60例样本，总样本量为1 751例。

1.2分析思路

在有针对性的研究设计框架之下，本研究的数据分析任务很明确。

第一，本研究所关心的结果变量为新媒体技术应用效果评分，取值为1～9，由于范围较窄，因此可以按照连续性变量加以分析，在此，我们不考虑频次表对实际取值范围的影响。

第二，由于该评分是从每一位受访者询问而来，因此研究中的基本观察单位就是受访者，除评分外，还记录了他们所选择的高校名称，8个省外高校和2个省内高校，构成了多组比较的结构。分析目的就是考察这10组受访者的平均评分有无差异。

第三，如果按照均数比较的方式考虑，则基本上应当考虑方差分析，因为这里是10组均数的比较，两两比较需要进行45次，因此不宜采用两两t检验，否则得到的结论可能不准确，因为会因放大某类错误而得到假阳性的比较结果。

第四，除主要影响因素外，本研究还需要考虑城市影响因素。在进行高校之间均数的比较时，还应当去除城市的影响：如果城市和高校之间不存在交互作用，则直接在模型中控制城市的影响即可；反之，如果两者之间存在交互作用，则可能需要分析城市进行高校的比较［1］。

下面我们将按照上述思路进行分析。

2　数据理解

2.1研究设计框架复查

首先应当了解分析所用的数据是否和实验设计框架一致，这里我们用交叉表过程来完成。如表1所示。

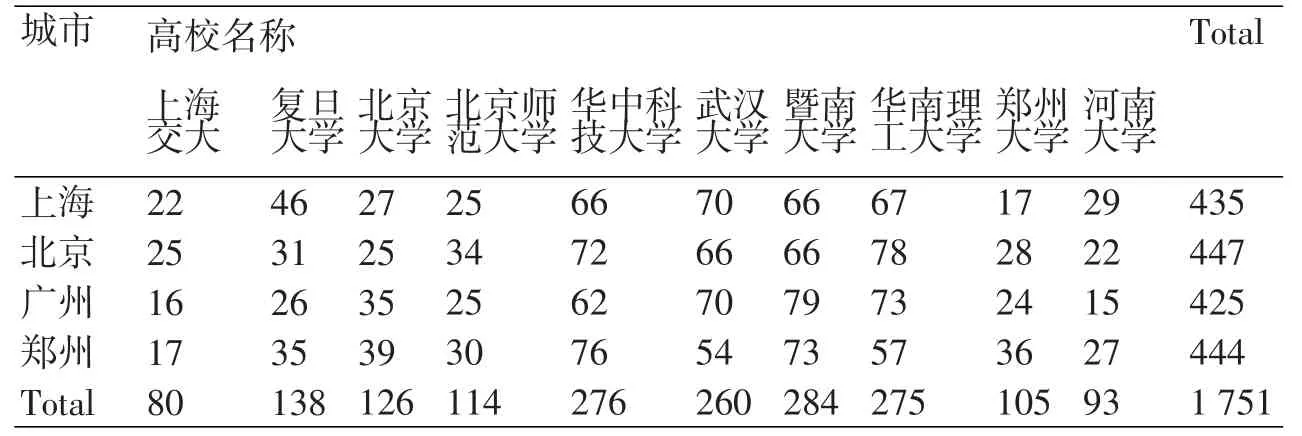
表1　城市*高校名称Crosstabulation

从表格中可以清楚地看到，每个城市×高校单元格内都有10～80例样本，不存在空单元格，因此整个研究设计是平衡的，符合普通方差分析模型的要求。

2.2均值的列表描述

下面考虑对各因素不同水平的新媒体技术应用测试评分均值进行考察，由于是分组描述，可以有两种实现方式：一种是首先按照各因素的不同水平进行样本拆分，然后对拆分的样本进行描述；另一种则是直接采用均值过程来完成此任务，此处采用后一种方式进行分析，由于城市、高校名称是并列选入“Independent list”的同一层而不是不同层，因此均值将分别按照城市和高校名称进行计算，结果如表2所示。

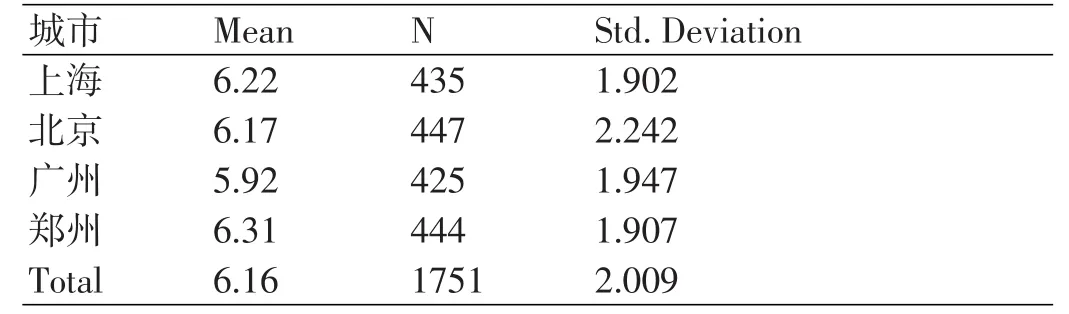
表2　新媒体技术应用评分城市

平均而言，上海和郑州对所有高校的新媒体技术应用评分偏高，广州的评分偏低。这种差异有可能反映的是不同城市受访者对新媒体技术应用的接受程度，这在本研究中不是核心问题。此外，可以发现北京的评分标准差要略高于其余3个城市，从新媒体技术普及程度的角度来理解，作为首都，北京本身就是南北的汇聚之地，受访者接受新事物高于其余城市也是可以理解的［2］。

表3　新媒体技术应用评分*高校名称

表3显示了用于对比的高校表现的好坏，受访者对暨南大学、复旦大学、河南大学的评价较高，均超过6分，河南省内的两所大学表现也不错，其中河南大学的均值为6.32分，在10组里面排名靠前，但是否具有统计学差异则不是现在的均值描述所能够回答的。

2.3均值的图形描述

对于各组的均数，一般可以使用箱图、条图等图形工具来考察。通常情况下箱图是首选工具，但由于新媒体技术应用评分为9分制，取值类别太少，采用箱图的呈现效果不佳，因此这里我们采用带误差线的条图来呈现，如图1所示。

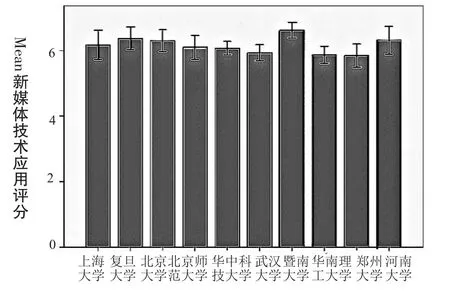
图1　绘制的误差线条图

图1所反映的信息和表3接近，但是更为直观，可见暨南大学和复旦大学的新媒体技术应用评分位列前茅，且各组的离散程度相差不大。

3　不同高校的评分差异分析

首先考察不同高校之间的评分是否存在差异，该问题可归纳为一般线性模型框架下的方差分析。在进行分析时，为了避免城市这一因素对结果造成影响，考虑对每个城市的样本数据分别进行分析，相应数据的拆分既可以通过选择个案来实现，也可以通过拆分文件来实现，这里我们采用效率更高的后者。

3.1单因素方差分析模型简介

3.1.1模型结构。以本研究案例的数据为背景，每一位受访者对新媒体技术应用的评分Yij可以表达为如下形式：Yij=μi+εij。其中，Yij代表第i个高校组中第j位受访者的评分。显然，在此表达式中μi表示某个品牌组的平均评分，i的取值范围为1～10，分别代表10所高校；而εij表示第i组的第j位受访者的随机误差，反映的是因各种原因导致的该受访者的实际评分和该组平均评分之间的差异。

为了统计推断的需要，以上模型一般被改写成更为标准的形式：Yij=μ+αi+εij。其中，μ表示总体的平均水平；αi表示影响因素在i水平下对应变量的附加效应，并假设所有αi之和应当为0；εij为一个服从正态分布N（0，σ2）的随机变量，代表随机误差。一般情况下，我们做假设检验实际上就是检验各个αi是否均为0，若均为0，即各组总体均数都相等，则当此假设成立时，Yij就会成为服从正态分布N（0，σ2）的一个变量。

3.1.2模型检验。方差分析模型中的检验可以分为总模型检验和各因素检验。对于总模型，所检验的假设如下。

H0：模型中涉及的因素的实际影响均为0，即除常数项外，任何参数αi、βj…均等于0。

H1：模型参数中至少有一个参数不等于0.

对于每一个因素所进行的检验，相应的假设如下。

H0：对任意的i取值，都有αi=0。

H1：至少有一个αi≠0。

对于单因素方差分析模型，显然上述两种检验是完全等价的。

在具体的检验实现方法上，方差分析的基本思想是变异分解，即将样本的总变异分解为若干部分，除一部分代表随机误差的作用外，其余每个部分的变异分别代表某个影响因素的作用。通过比较可能由某因素所致的变异与随机误差的大小，再借助F分布做出推断，即可了解该因素对结果变量的影响是否存在。

3.1.3单因素方差分析模型的应用条件。统计学中的方法或许有成千上万，但没有哪种方法是放之四海而皆准的，自然这里的方差分析也不例外。一般来说，要应用方差分析，数据应当满足以下几个条件，或者说以下的假设应当成立。

观察对象来自所研究因素的各个水平之下的独立随机抽样。

每个水平下的因变量应当服从正态分布。

各水平下的总体具有相同的方差。

上述三点一般会被简单地概括为独立性、正态性和方差齐性，而在具体考察适合条件时，应当以模型残差来进行考察。

3.2高校作用的总体检验

第一行的校正模型是对所用方差分析模型的检验，其原假设为模型中所有的影响因素均无作用，即高校间均无差异。以北京为例，该检验的P值远小于0.05，因此所用的模型有统计学意义。纳入模型的影响因素中至少有一个是有作用的，由于模型中只有高校这一个影响因素，因此等价于品牌有影响。

第二行是对模型中常数项是否等于0进行检验，显然它在本研究中没有实际意义，故不作考虑。

第三行专门针对高校的作用进行了检验，其原假设为所有αi均等于0。由于本研究中只有高校这一个影响因素，因此这里的分析结果应当完全等价于前面对模型的检验，可见高校在这里有统计学意义，即不同高校的新媒体技术应用评分是不同的。

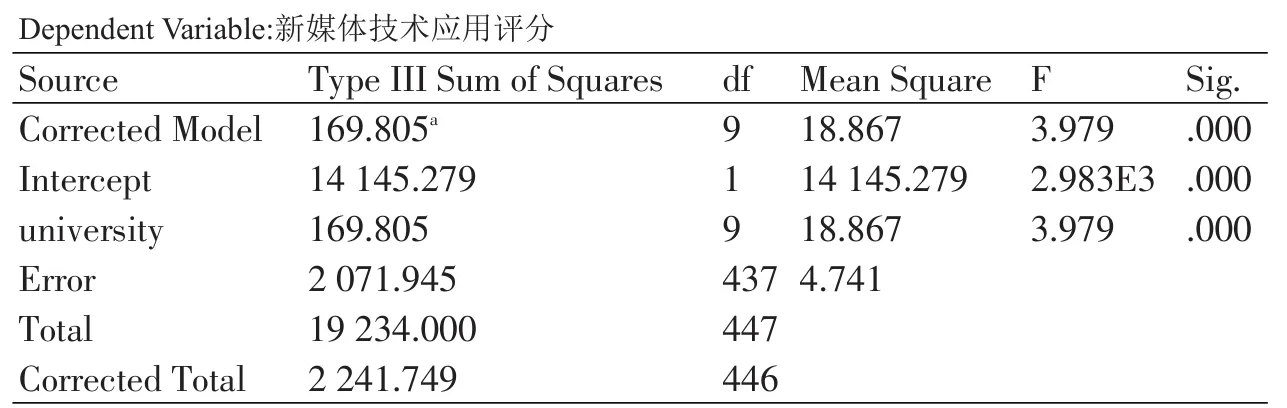
表4　主体间效应的检验（北京）

3.3组间两两比较

3.3.1具体操作。上面的结果表明高校间是有差异的，但究竟是哪些高校之间有差异呢？为了进一步回答问题，在方差分析后需要使用两两比较方法进一步分析。这里我们采用比较常见的SNK法进行两两比较。相应的分析结果如表5。

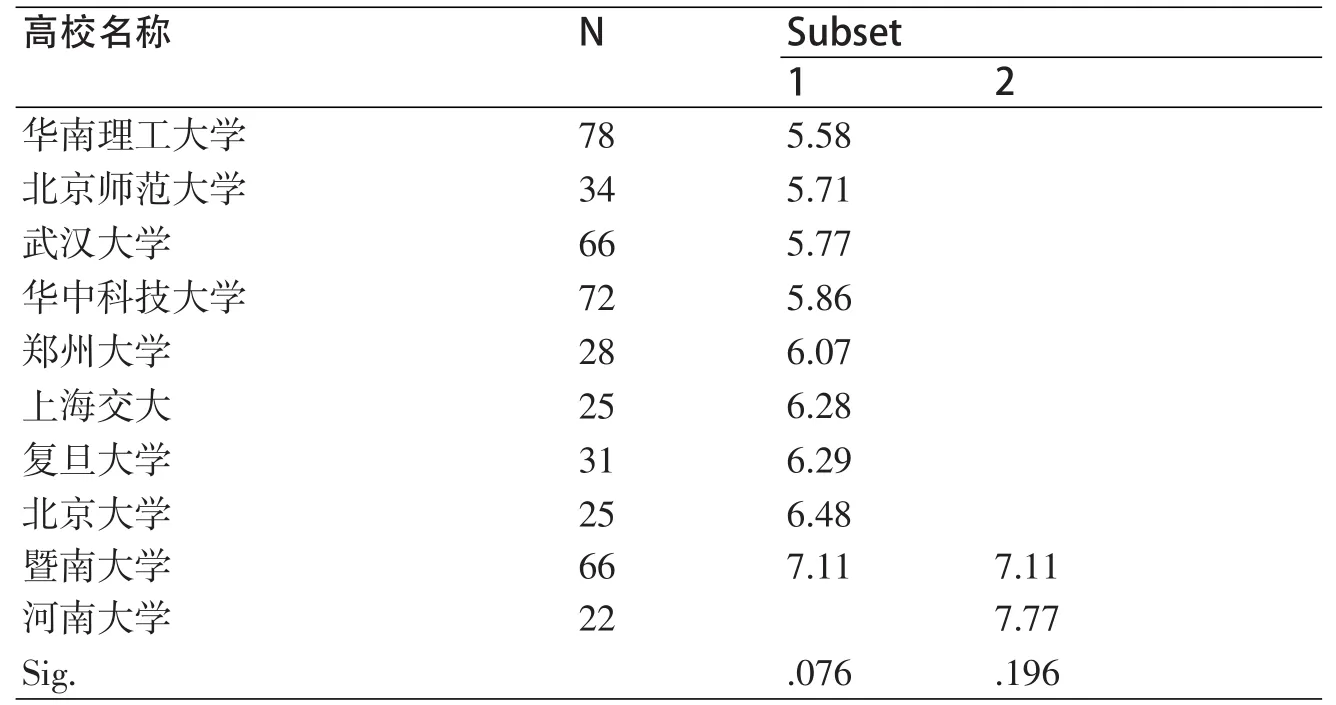
表5　新媒体技术应用评分（北京）

表5是用S-N-K法进行两两比较的结果，该方法的输出比较特别。简单地说，首先它会将各组在表格的纵向按照均数大小排序，然后表格的横向被分成若干个亚组（Subset），不同亚组间的P值小于0.05，而同一亚组内的各组均数则两两无差别，比较的P值均大于0.05。从表5中可见，10所高校被分在两个不同的亚组中，第一亚组包括除河南大学外的其余9所高校，在该列的最下方可见本亚组的检验P值为0.076，显然处于界值附近；第二亚组则包含了河南大学和暨南大学，组内检验P值为0.196。如果两所高校被分在完全不同的亚组中，则它们的均数有统计学差异，例如华南理工和河南大学，或者北京师范大学和河南大学均如此。

3.3.2两两比较方法的选择问题。

S-N-K即Student Newman Keuls法，是运用最广泛的一种两两比较方法。它采用Student-Range分布进行所有组均值间的配对比较。该方法保证在H0真正成立时总的α水准等于实际设定值，即控制了一类错误。但根据近年来的研究发现，当两两比较的次数极多时，该方法的假阳性非常高，因此当比较次数较多时，我们对本研究采用的S-N-K法得到的有统计学意义的结论持谨慎的态度。

本文所提出的互助外语导游创业模式由于是依托于互联网平台的，基于导游自由执业的背景下采取预约导游服务模式，即旅游者预约平台预定导游为其提供服务。作为线上创业模式，首先要重视的便是企业内部的管理制度建设。作为线上平台要与国家旅游局的“全国导游公共服务监管平台”进行对接，配合相关部门依法依规进行外部管理和监督；此外，平台应当时刻重视自查，强化对导游的审查义务和监管责任，完善游客对导游的评价反馈机制，增强应对突发情况时的紧急处理能力。

3.4方差齐性检验

表6　误差方差等同性的Levene检验

前面我们说到过方差分析模型也有独立性、正态性、方差齐性等要求。对于独立性，从本研究设计或者数据背景可以进行大致评估；正态性可以在选项中绘制残差图来考察，不过对单因素方差分析模型而言，残差分析的实际价值不大；真正比较重要的是方差齐性的要求，在单变量GLM过程的选项中，可以要求进行方差齐性检验，从而检查结果来考察模型是否满足方差齐性的要求，如表6所示。

以上输出以北京数据的方差齐性检验分析结果，此处的无效假设为：各组方差齐性。可见P值为0.168，大于0.05，因此尚不能拒绝该无效假设，即可以认为方差齐性。

4　两因素方差分析模型分析

上面我们分4个城市分别考察了高校的影响，可以发现在每个城市中高校间的差异并不完全一致，那么就整体而言高校之间有无差异呢？对本研究项目而言，将所有信息整合起来得到一个综合的结果是非常必要的，虽然最简单的做法是忽略城市区别，将样本直接综合起来进行单因素方差分析，但这样做太过于粗糙了。本研究项目将进一步研究同时考虑城市和高校两个因素的方差分析模型。

4.1两因素方差分析模型简介

4.1.1多因素方差分析模型的结构。前面我们已经介绍了单因素方差分析模型的基本结构，在多因素方差分析模型中，其原理没有任何变化，只是模型中考虑的因素更多而已。下面我们以本研究项目的两因素方差分析模型为例进行介绍，其公式如下：Yijk=μ+αi+βj+εijk。

其中，αi、βj分别表示A因素i水平和B因素j水平的附加效应，εijk仍为随机误差变量。

更为复杂的是考虑交互作用的情形，模型如下：

其中，αi、βj分别表示A因素i水平和B因素j水平的附加效应。αiβj则为两者的交互效应。

4.1.2方差分析模型的检验。方差分析模型中的检验可分为总模型的检验和各因素的检验。

对于总模型，所检验的假设如下：

H0：模型中所涉及因素的实际影响均为0，即除常数项外，对于任何参数αi、βj…均等于0.

H1：模型参数中至少有一个参数不等于0.

而对每个因素进行的检验，相应的假设如下：

H0：对任意的i取值，都有αi=0。

H1：至少有一个αi≠0。

在具体检验方法上，方差分析的基本思想是变异分解，即将样本的总变异分解为若干部分，除一部分代表随机误差的作用外，其余每个部分的变异分别代表某个影响因素的作用，通过比较可能由某因素所致的变异与随机误差的大小，在借助F分布做出推断，即可了解该因素对结果变量的影响是否存在。

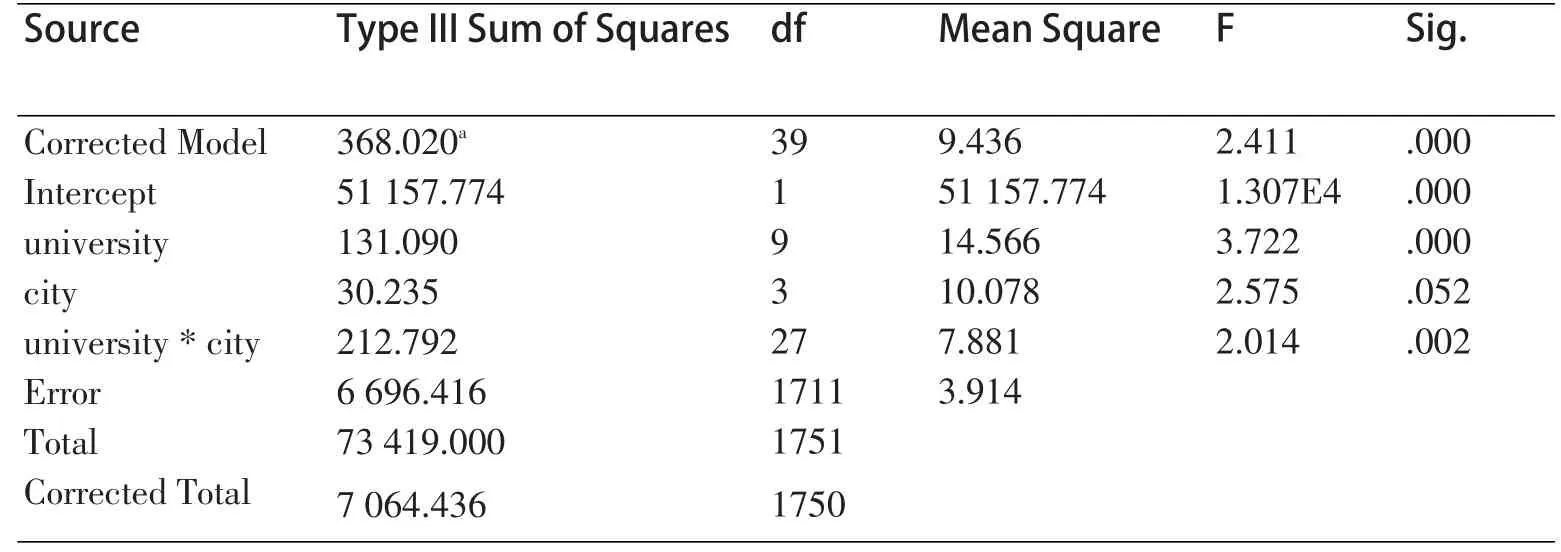
表7　主体间效应的检验

4.2拟合包括交互项的饱和模型

下面我们使用单因素过程来建立本研究项目的两因素方差分析模型，其方差分析如表7所示。

表7就是结果中最为重要的方差分析表，可见在其中进行了多个检验，依次解释如下：

第一行的校正模型是对所用方差分析模型的检验，其原假设为模型中所有的影响因素均无作用，即城市间、高校间均无差异，两者的交互作用不存在。该检验的P值远小于0.05，因此所用的模型有统计学意义，以上所提到的影响因素中至少有一个是有差异的，具体是谁有差异我们看下后面的分析结果。

第二行是对模型中常数项是否等于0进行的检验，显然它在本次分析中没有实际意义，忽略即可。

第三、四行分别是对城市间、高校间差异进行的检验，可见两者均有统计学意义。

第五行是对城市和高校的交互作用进行检验，可见P值为0.002，无统计学意义。

4.3拟合只包含主效应的模型

由于在本研究项目分析中发现两个因素的交互作用无统计学意义，为了使模型更为简洁，需要在模型中将其去除，具体操作在模型子对话框中实现。新的分析结果如表8所示。

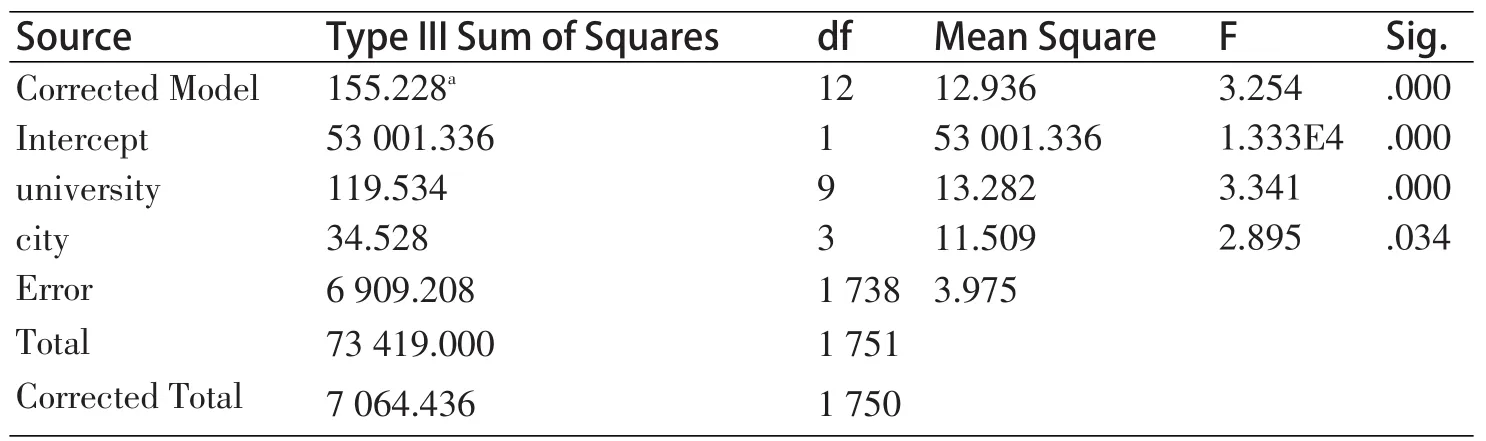
表8　主体间效应的检验

表8就是结果中的方差分析表，依次解释如下：

第一行的校正模型是对所用方差分析模型的检验，其原假设为模型中所有的影响因素均无作用，即城市间、高校间均无差异，两者的交互作用不存在。该检验的P值远小于0.05，因此所用的模型有统计学意义。

第二行是对模型中常数项是否等于0进行的检验，显然它在本次分析中没有实际意义，忽略即可。

第三、四行分别是对城市间、高校间差异进行的检验，可见两者均有统计学意义。

由表8可见，对模型、城市、高校的检验结论相同，即不同城市对同一种样品的平均评分不同，并且在同一城市中，受访者对不同高校样品组的平均评分也不同。

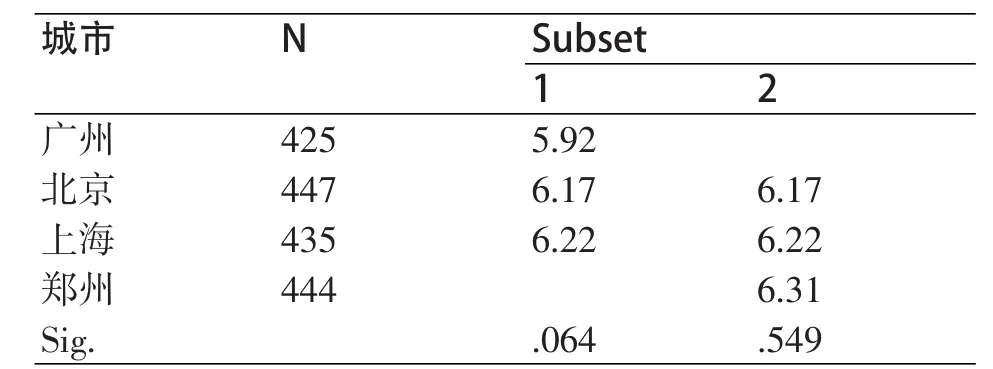
表9　新媒体技术应用评分

4.4组间两两比较

通过分析，我们已经得知城市间、高校间的评分是有差异的，为了能够回答究竟是哪些城市、高校间有所不同，下面用SNK法进行两两比较。

表9显示了4个城市被分为两个亚组，但是北京、上海同时跨了两组，按照严格的统计解释，结论应当为：广州和郑州的平均评分有差异，其余两两无差异。这是多组两两比较中常出现的结果，但是在我们的应用上会带来混乱，为此我们需要在统计结论的基础上结合本研究项目的实际再进一步。考察两个亚组内部的P值，第一亚组内部检验P值为0.064，非常接近0.05；第二亚组的P值为0.549。再观察4个城市的评分均数，显然北京、上海的均数更加接近郑州，从应用的角度出发，最终的结论为：广州的评分低于另外3个城市，另外三者则两两无差别，如表10所示。

表10显示了10所高校可以被分为两个亚组，第一亚组由郑州大学、华南理工大学、武汉大学、华中科技大学、北京师范大学、上海交大、北京大学、河南大学和复旦大学这9所高校组成，组内检验的P值为0.412，远大于界值0.05；第二组由武汉大学、华中科技大学、北京师范大学、上海交大、北京大学、河南大学、复旦大学和暨南大学组成，组间检验的P值同样大于0.05。

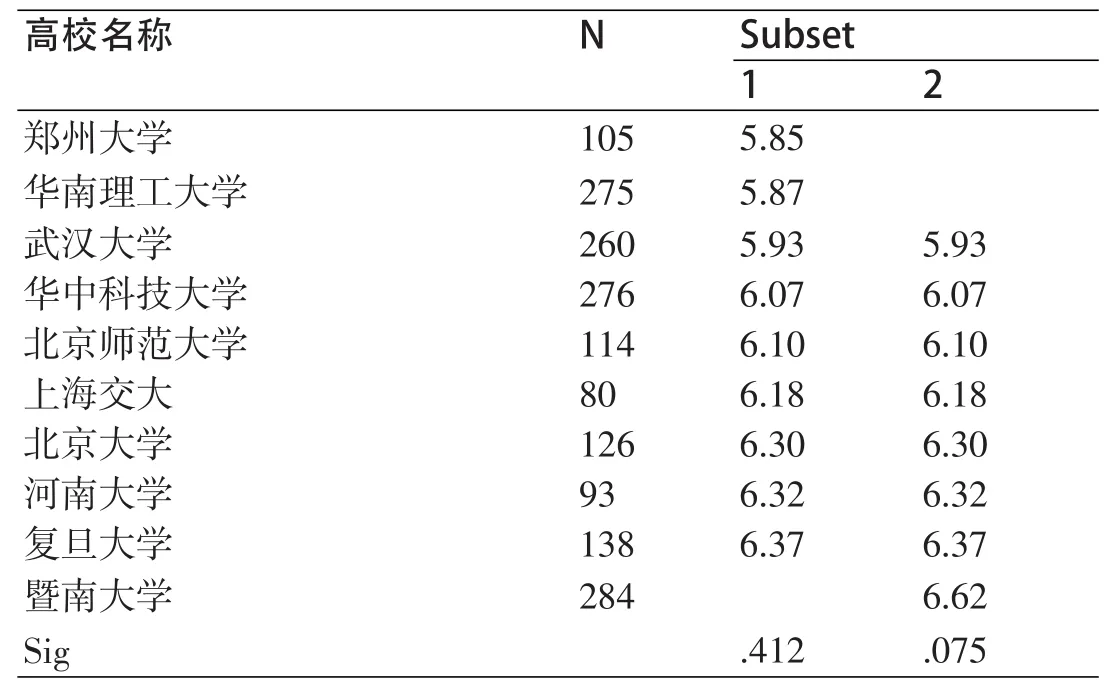
表10　新媒体技术应用评分

4.5随机因素分析

在本研究项目中，我们将高校和城市均设定为固定因素，对高校而言，我们只希望比较10所高校中哪个受新媒体技术影响的程度更深，没有任何问题。但是对城市而言，如果我们只分析4个城市间的新媒体技术影响有无差异，则以上分析结果是正确的［3］；但是如果实际目的是通过4个城市来推断全国所有同类城市的新媒体技术影响有无差异，则这里涉及将结果外推到未出现在样本中的其他城市的问题，它就应当是一个随机因素。换言之，这里的分析结果只能说在这4个城市间是有效的，但不能代表全国其他城市的情况。

4.5.1固定因素与随机因素。两者都是因素的不同种类，固定因素指的是该因素在样本中所有可能的水平都出现了。换言之，该因素的所有可能水平仅此几种，针对该因素而言，从样本的分析结果可以得知所有水平的状况，无须进行外推［4］。

和固定因素相对应的是随机因素，它是指该因素所有可能的取值在样本中并没有全部出现，或不可能全部出现。换言之，目前在样本的这些水平是从总体中随机抽样而来，如果重复本研究，则可能得到的因素水平会和现在完全不同！我们显然希望得到的是一个能够“泛化”，即对所有可能出现的水平均适用的结果。一般来说，固定因素和随机因素在分析时应分别指定，如果将随机因素按固定因素来分析，则可能得出错误的分析结果。很多时候，判断一个因素究竟是固定因素还是随机因素并不是很容易的事。

4.5.2具体分析操作。下面我们考虑将城市指定为随机因素进行分析，如表11。

在本研究项目中，分析的重点放在4个抽样城市，则将城市作为固定因素分析是合理的，结论只是在相应的4个城市中有效，否则就应当将城市作为随机因素进行分析。如果将城市错误地指定为固定因素，则分析结果并不能外推到其他城市，有时候还会得到错误的结论。

5　分析结论

综上分析，本研究项目的基本结论如下：

第一，在10所高校中，大致可分为两个评价层次，新媒体技术应用影响评分较高的是暨南大学、复旦大学、河南大学、北京大学、上海交大、北京师范大学、华中科技大学和华中科技大学，它们之间无差异。河南省内高校——河南大学在新媒体技术影响测试中效果还是令人满意的［5］。

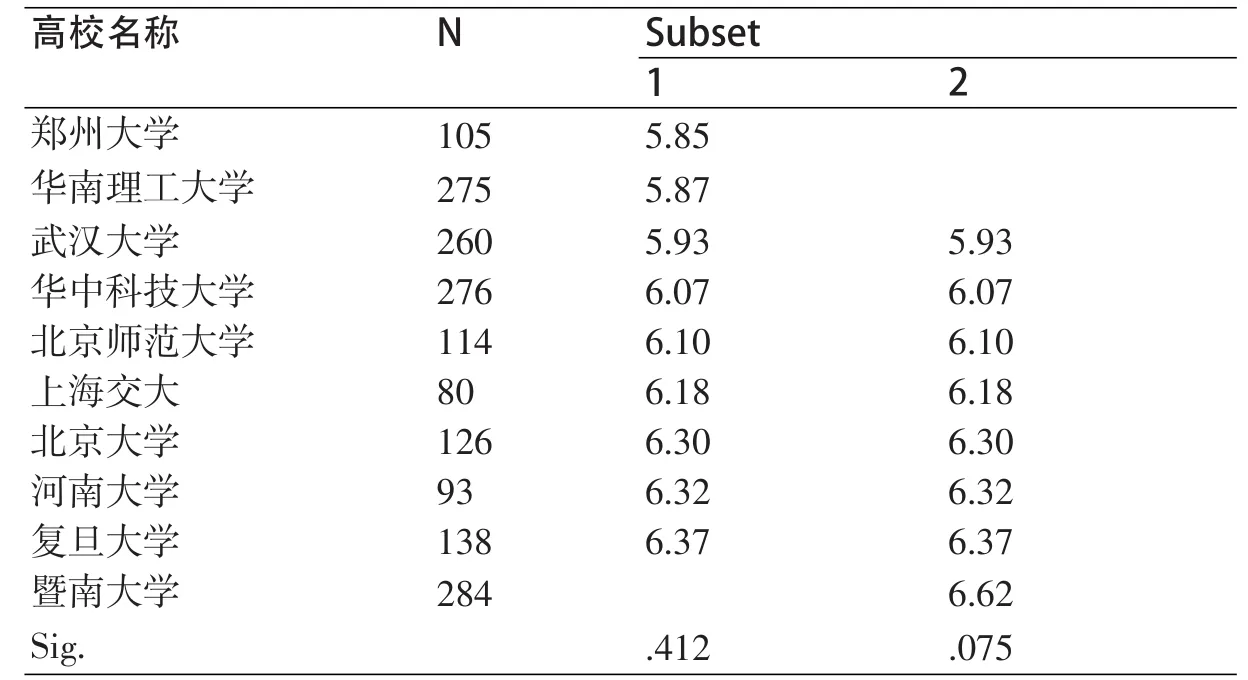
表11　主体间效应的检验

第二，在研究涉及的4个城市中，受访者对相同样品的评分有所差异，广州的平均评分低于北京、上海和郑州。

第三，本次研究中未发现高校和城市间存在交互作用，即新媒体技术高校影响评分间的差异在不同城市间是相同的，尚未发现特殊的地域偏好。

参考文献：

［1］杜俊峰.新媒体技术对大学生思想政治教育的影响及对策研究［J］.渤海大学，2014.

［2］姜玉莲.微课程研究与发展趋势系统化分析［J］.中国远程教育，2013，12.

［3］吴万伟.“慕课热”的冷思考［J］.复旦教育论坛，2014，1.

［4］金秀舫.新媒体环境下以就业市场为需求的高教改革［J］.中国报业，2012，2.

［5］宋专茂.慕课何以致高校教学方法革新［J］.复旦教育论坛，2014，4.

Analysis on the Impact of New Media Technology Factors on College and University

Hou Dongqing1Yin Jun2
（1.School of Journalism and Communication，Henan SIAS International College of Zhengzhou University Zhengzhou Henan 451150；2. Henan science and Technology Information Research Institute，Zhengzhou Henan 450003）

Abstract：New media technology has brought major changesto the teaching structure，teaching mode and teaching means of the entire teaching system，then how much influence does new media technology exactly produce on higher education，and how will the influences reactin our real life，this paper briefly discussed their mutual influences.

Key words：new media technology；network environment；education；factors

作者简介：侯冬青（1979-），男，硕士，讲师，研究方向：网络与新媒体；尹君（1969-），男，本科，工程师，研究方向：科技情报。

基金项目：2016年河南省科技厅科技攻关项目“DashBoard在新闻可视化报道中的应用研究”（162102310383）。

收稿日期：2016-2-6

［中图分类号］G641

［文献标识码］A

文章编号：1671-0037（2016）03-39-6