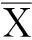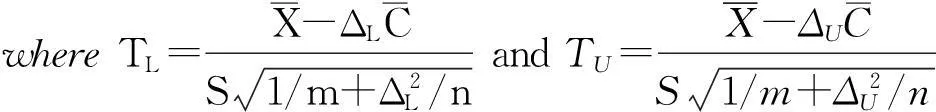Equivalence tests to support environmental biosafety decisions:theory and examples
2016-06-02DavidANDOWGborVEIboraPiresPAULA
David A. ANDOW, Gbor L. LÖVEI, Débora Pires PAULA
1DepartmentofEntomology,UniversityofMinnesota,St.Paul,MN55108,USA;2DepartmentofAgroecology,AarhusUniversity,FlakkebjergResearchCentre,DK-4200Slagelse,Denmark;3EmbrapaGeneticResourcesandBiotechnology,ParqueEstaçãoBiológica,W5Norte,P.O.Box02372,Brasília,DF, 70770-917,Brazil
Equivalence tests to support environmental biosafety decisions:theory and examples
David A. ANDOW1*, Gbor L. LÖVEI2, Débora Pires PAULA3
1DepartmentofEntomology,UniversityofMinnesota,St.Paul,MN55108,USA;2DepartmentofAgroecology,AarhusUniversity,FlakkebjergResearchCentre,DK-4200Slagelse,Denmark;3EmbrapaGeneticResourcesandBiotechnology,ParqueEstaçãoBiológica,W5Norte,P.O.Box02372,Brasília,DF, 70770-917,Brazil
Abstract:A major role of ecological risk assessment (ERA) has been to provide scientific guidance on whether a future human activity will cause ecological harm, including such activities as release of a genetically modified organism (GMO), exotic species, or chemical pollutant into the environment. This requires the determination of the likelihoods that the activity: would cause a harm, and would not cause a harm. In the first case, the focus is on demonstrating the presence of a harm and developing appropriate management to mitigate such harm. This is usually evaluated using standard hypothesis analysis. In the second case, the focus is on demonstrating the absence of a harm and supporting a decision of biosafety. While most ERA researchers have focused on finding presence of harm, and some have wrongly associated the lack of detection of harm with biosafety, a novel approach in ERA would be to focus on demonstrating directly the safety of the activity. Although, some researchers have suggested that retrospective power analysis can be used to infer absence of harm, it actually provides inaccurate information about biosafety. A decision of biosafety can only be supported in a statistically sound manner by equivalence tests, described here. Using a 20% ecological equivalence standard in GMO examples, we illustrated the use of equivalence tests for two-samples with normal or binomial data and multi-sample normal data, and provided a spreadsheet calculator for each. In six of the eight examples, the effects of Cry toxins on a non-target organism were equivalent to a control, supporting a decision of biosafety. These examples also showed that demonstration of equivalence does not require large sample sizes. Although more relevant ecological equivalence standards should be developed to enable equivalence tests to become the main method to support biosafety decision making, we advocate their use for evaluating biosafety for non-target organisms because of their direct and accurate inference regarding safety.
Key words:GM crops; average bioequivalence; environmental impact; ERA; statistical methods
Introduction
A major role of ecological risk assessment (ERA) has been to provide scientific guidance on whether a future human activity will cause ecological harm (Suter,2006). These activities may include land use changes, such as rural and suburban development, agricultural expansion, or deforestation, the release of organic and inorganic chemicals, such as CO2, NOX, pesticides and other toxic chemicals, and the release of biological organisms, such as biological control organisms, exotic species, and genetically modified organisms (GMOs). The logic of all of these ERAs directs the assessments to determine the likelihood that the activity would cause an adverse environmental change, and at the same time the likelihood that the activity will not cause an adverse environmental effect. A risk assessor is interested in both the probability that there will be an adverse effect(s) and the probability that there will be no adverse effect(s). The first of these can be determined by standard statistical hypothesis tests. In the case of "no harm", the assessor must be able to conclude that a test treatment has similar risk or effect as the control treatment, i.e. the two are equivalent, and this requires the use of equivalence tests, described here.
Under standard experimental design and statistical hypothesis testing, the null hypothesis is that the responses to the test and control treatments are the same. Rejecting the null hypothesis (that they are the same) will lead to the conclusion that they are different. In other words, it allows a conclusion that there is a difference between the two treatments, but it does not allow a conclusion that they are the same or similar. Equating the lack of statistical significance with "no difference" or biosafety is a serious logical flaw, because the lack of significance can be related to low replication and/or high error variation, not because there is truly no effect. Inability to reject the null hypothesis can lead to a Type Ⅱ error (= not rejecting the null hypothesis when in fact the treatments are different). For any given estimated difference between the treatments, as the estimated standard error of the difference increases from 0, the result will eventually change from an inference of significant difference to one of equivalence, which is the opposite of what is desired for equivalence testing. For the most part, this problem — that the null hypothesis cannot be proved with standard hypothesis testing — is recognized, but because alternatives are not recognized it is largely ignored (e.g., Raybould,2010).
In recent decades, however, a new branch of statistical theory, equivalence testing, has been developed to address these problems. An equivalence test inverts the null and alternative hypotheses, so that the null hypothesis is that the treatments are different and the alternative hypothesis is that they are equivalent. Thus the rejection of the null hypothesis enables a sound statistical inference that the treatments are equivalent. Equivalence tests have gained widespread use for supporting regulatory decisions about new generic drugs, and there are now textbooks for conducting such tests (e.g., Patterson & Jones,2005). In this paper, we summarize the statistical theory underlying equivalence tests, compare this approach with standard hypothesis testing and power analysis, illustrate how to conduct these statistical tests with examples from ecological risk analysis experiments for testing the safety of GM crops, and suggest that equivalence testing is superior to standard hypothesis testing for assessing ecological safety. We use GM crops because we have conducted research in this area. A spreadsheet calculator for the equivalence tests described in this paper is provided in the supplementary material. Even though the examples are solely related to GMOs, the potential scope of application of equivalence tests in ecological risk assessment and environmental policy is quite broad (Diamondetal.,2012; Hanson,2011; Kristofersson & Navrud,2005).
Statistical theory for equivalence tests
There are three kinds of equivalence tests: average equivalence, population equivalence and individual equivalence (Liu & Chow,1996). Average equivalence evaluates the similarity in the average response between a test and control treatment. Population equivalence evaluates the similarity in the entire statistical distribution (average, variance, skew, kurtosis, etc) of the responses to the treatments. Population equivalence is a more rigorous similarity standard than average equivalence because the average, variance, and possibly higher statistical moments all must be similar. Individual equivalence tests examine the similarity in the responses to the treatments within the same individuals. This last is often used in drug testing, where each individual is exposed to both treatments with a suitable re-equilibration period between treatments (a so-called two-period crossover design), and also includes other designs, such as repeated measures, and paired designs. From such a design it is possible to evaluate equivalence individual by individual.
For ecological risk assessment, average equivalence is the more generally applicable of the three. Individual equivalence testing will be limited because it is often be difficult to expose individuals to more than one treatment, especially in a toxicity assay. Population equivalence testing will also be limited because it is usually not possible to have sufficiently high replication to test for equivalence in variance, skewness, etc.
Equivalences tests can be understood by contrasting them with standard hypothesis tests (Fig.1). If the average response of some biological entity to a test treatmentiis denotedμiand the average response to the control treatment (negative control) isμc, a standard hypothesis for normally distributed data is
H0:μi/μc=1Ha:μi/μc<1 orμi/μc>1
[1]
whereH0is the null hypothesis andHais the alternative hypothesis. The null hypothesis is that the two populations have the same mean, and the alternative hypothesis is that they do not.
An equivalence hypothesis reverses the null and alternative hypotheses. Using the same notation, the analogous equivalence hypothesis is
[2]
wherethevaluesΔLandΔUareequivalencestandardssetaccordingtoregulatory,statisticalandbiologicalconsiderationsthatdefinehowclosethemeansmustbetobeconsideredequivalent.Thenullhypothesisstatesthattheratiooftheaveragesiseitherlessthanthelowerorgreaterthantheupperequivalencestandard,andthealternativehypothesisisthatthevalueoftheratioisbetweenthetwostandards.Notethatthehypothesisthattheaveragesarethesame,isnowapartofthealternativehypothesis.Theequationsin[2]aretypicallyreformulatedas:
H01: 0≥μi-ΔLμcversusHa1: 0<μi-ΔLμc
H02: 0≤μi-ΔUμcversusHa2: 0>μi-ΔUμc
[3]
Thenullhypothesisin[2]isrejectedandthemeansareequivalentifandonlyifbothnullhypotheses[3]arerejected.Forsomeregulatoryprocedures, ±20%isacommonlyusedequivalencestandard(ΔL=0.80andΔU=1.25).
Whenequation[2]islog-transformed,linearhypothesesareproduced:
H0: θL≥ηi-ηcorηi-ηc≥θU
Ha: θL<ηi-ηcandηi-ηc<θU
[4]
whereη=ln(μ)andθ=ln(Δ).IntheUSandEurope,thevalueθU=-θL=0.223144isrequiredformostgenericdrugtests,whichisthesameas±20%ontheuntransformedscale.
Hypotheses[2]~[4]arecalledintersection-unionhypotheses(Berger&Hsu,1996a).Thenullhypothesisistheintersectionoftwoone-sidedhypotheses,andthealternativehypothesisistheunionoftwoone-sidedhypotheses.Atestofanintersection-unionhypothesisiscalledanintersection-uniontest(IUT)andisoftenformulatedasatestoftwoone-sidedhypotheses,whichiscalledatwoone-sidedtest(TOST).TheformulationofanequivalencetestasanIUTallowstheapplicationofsomegeneralmathematicaltheoremstodeterminetheTypeⅠerrorrateforthetest(Berger,1982;Berger&Hsu,1996a).AlthoughitmightbethoughtthattheTypeⅠerrorrateforthetwotestswouldneedtobeadjustedbecausetherearemultipletestswiththesamedata,thetheoremsprovethatsuchcorrectionsarenotneededforanyofthetestsdiscussedinthispaper(Berger,1982;Berger&Hsu,1996a).
Anothertheorem(Theorem4,Berger&Hsu,1996a)providesconditionsforconstructingconfidenceintervals(orregions)onthestatisticalparameter(s)sothatconfidenceintervals(orregions)canbeusedtotestequivalenceinlieuofhypothesistesting.IfandonlyifanIUTrejectsthenullhypothesiswithaTypeⅠerrorof0.05,the95%confidenceintervalaroundηi-ηrwillbeentirelycontainedintheinterval[θL, θU],whichiscalledtheequivalenceregionorinterval.Thisdemonstratestheidentitybetweenhypothesistestingandinterpretationofconfidenceintervalsandregions.Wewillusethistheoremtotesttheequivalenceofmultipletesttreatmentstoasinglecontroltreatment.
Comparisonwithretrospective(observed)power
AretrospectiveanalysisofthestatisticalpowerofanexperimenthasbeenproposedtoaddresstheproblemofTypeⅡerrorinGMOecologicalriskassessment(e.g.,Romeiset al.,2011).ThepowerofanexperimentaldesignisanestimateoftheprobabilityofnotmakingaTypeⅡerror(notrejectingthenullhypothesis,wheninfactitshouldhavebeenrejected).Therearetwokindsofpoweranalysis:prospectiveandretrospective.Prospectivepoweranalysisusesinformationfrompreviousexperimentstooptimizethedesignofexperimentsyettobeconducted,andisalegitimateandusefulstatisticaltool(Hoenig&Heisley,2001).Itcanalsobeusedtooptimizeequivalencetests.
Hoenig&Heisley(2001)provideadeepcritiqueofretrospectivepoweranalysis.RetrospectivepoweranalysisaimstoprovideanindependentestimateoftheprobabilityofnotmakingaTypeⅡerrorbasedonthedesignanddataofanexperimentthathasalreadybeencompleted,andreliesonastatisticcalled"observedpower".AdvocatesforretrospectivepoweranalysisarguethathighobservedpowerindicatesalowTypeⅡerrorrateandthereforethenullhypothesisismorelikelytobetruewhenitisnotrejectedandthereishighobservedpower(e.g.,Romeiset al.,2011).TheseargumentsandinferencesarelogicallyflawedbecauseretrospectivepoweranalysisdoesnotprovideanindependentestimateoftheprobabilityofnotmakingaTypeⅡerror(Brosi&Biber,2009;Nakagawa&Foster,2004;Perryet al.,2009).
Hoenig&Heisley(2001)providedaspecificexampletoillustratethisseriouslogicalflawintheuseofobservedpower.Supposetwosimilarexperimentsareconducted,andneitherrejectsthenullhypothesis,buttheobservedpowerinthefirstexperimentwaslargerthantheobservedpowerinthesecondone.Advocatesoftheuseofobservedpowermaywishtoinferthatthefirstexperimentgivesstrongersupportfavoringthenullhypothesisthanthesecond.However,thisleadstoafatallogicalcontradiction.Supposetheexperimentsweretestedwithaone-sidedt-test.Lettp1andtp2betheobservedteststatisticsfromtherespectiveexperiments.Becausetheobservedpowerwashigherinthefirstexperiment,thisimpliesthattp1>tp2,becauseobservedpowerisanincreasingfunctionofthetpstatistic.Butiftp1>tp2,thenthep-valuesfromtheexperimentswouldhavep1 Conductingequivalencetests Equivalencetestscanbeconductedformanydifferentexperimentaldesigns,andoneareaofactiveresearchisextendingtheiruseformorecomplexdesigns.Hereweprovideabasicintroductiontoequivalencetestsforsomecommonandsimpleexperimentaldesigns:twoindependenttreatmentsandnormaldata,twoindependenttreatmentsandbinomialdata,multipleindependenttreatmentsandnormaldata,andreplicationofexperimentswithmultipleindependenttreatmentsandnormaldata.WeuseexamplesforGMObiosafetytestingbecausewehavebeenconductingresearchinthisareaandcanuserealdatatoillustratetheuseofequivalencetests.Theseexamplesincludeonlyoneswherenosignificantdifferencewasdetectedusingstandardhypothesistests,andareusedtoillustratewhenitispossibletoconcludethatthereisstatisticalequivalencesupportingabiosafetydecisionandwhenthisisnotpossible. Normaldata TL>tα,νandTU<-tα,ν [5] [6] These have a Student′st-distribution withν=m+n-2 degrees of freedom. The TOST [3] is conducted using the ordinary,α=0.05, one-sidedt-test based onTLfor the one-sided hypothesis [3 upper] and the ordinary,α=0.05, one-sidedt-test based onTUfor the one-sided hypothesis [3 lower]. A numerical example is provided in Box 1 and the supporting information. Binomial data For binomial data there are several alternatives for constructing equivalence intervals and designating equivalence standards, based on the binomial parameter,π. They can be modeled on the arithmetic difference between the test (πi) and control (πc) parameters (πi-πc), the proportional difference in the parameters (πi/πc), or the proportional difference in the odds of a response (πi(1-πc))/((1-πi)πc), which is based on the odds ratios in each treatment. We calculated the equivalence interval for the three models (arithmetic, proportional, and odds ratio), and expressed it as the interval of the test treatment (πi) as a function of the control treatment (πc). The proportional difference model, which was ideal for normal data [2], is asymmetrical across the range ofπc(Fig.2), which is problematic because equivalence will depend on which response was chosen as the focal response. The others are symmetric (Fig. 2), but differ nearπr1=0 orπr1=1. Both can be justified, depending on whether the absolute differences or the difference in odds is critical. Here we provide equivalence tests for arithmetic differences with sufficiently large samples (m,n≥50), because these have a stable Type Ⅰ error rate (Chenetal.,2000). For small samples, exact methods are required (Agresti,1996). LetX1, …,Xmdenote the independent binomial responses (m,πi) to the test treatment andC1, …,Cndenote the independent binomial responses (n,πc) to the control treatment, whereπiandπcare the true response probabilities for the test and control treatments, respectively, andmandnare the number of independent observations for each. In addition, letycbe the total number of observed "positive" responses in the control treatment andxibe the number of "positive" responses in the test treatment, so thatn-ycandm-xi, respectively, become the number of "negative" responses in the two treatments. For the arithmetic difference in response probabilities, the equivalence hypothesis is H0:ΔL≥πi-πcorπi-πc≥ΔU Ha:ΔL<πi-πcandπi-πc<ΔU [7] whereΔLandΔUare equivalence standards determining how closeπiandπcmust be to be considered equivalent. For drug testing, the standards used vary between 10%~20%, but here we set the standards asΔL=-0.2 andΔU=0.2, withπiandπcbounded by the interval [0, 1]. More generally, the equivalence intervals can be adjusted based on the observed values ofπiandπc. A TOST for [7] comes from the asymptotic test statistic for the difference between two binomial parameters,πi-πc, and is based on the following two statistics with a standard error estimated by maximum likelihood (Farrington & Manning,1990), [8] Fπ(p)=πyr(1-π)n-yr(π+Δj)xi(1-π-Δj)m-xi Iπ=[max{0,-Δj},min{1,1-Δj}] [9] zFM,LandzFM,Uareχ2-distributedwith1degreeoffreedom.Thetwotreatmentsareequivalentifbothone-sidedtestsarerejectedatapredeterminedlevelofα,usuallyα=0.05,thatis,if zFM,L>3.841andzFM,U>3.841 [10] whicharetheupperandlowerα=0.05tailsofthestandardnormaldistribution. Multiplecomparisonstoacommoncontroltreatment Inecologicalriskassessment,experimentsfrequentlyhavemorethanonetesttreatmentcomparedtoasinglecontroltreatment,requiringastatisticalprocedureformakingmultiplecomparisons.Thestatisticaldesignisacompletelyrandomizedone-waytreatmentstructure,x=Dβ+ε,wherexisthevectorofmeasuredresponses,Distheknowndesignmatrix,βisavectorofunknownfixedeffects,whichisestimatedbythetreatmentmeans,andεisarandomerrorvectorwithE[ε]=0.Onesolutionistouseequivalencetestsbasedonconfidenceintervalsdesignedformultiplecomparisons(Berger&Hsu,1996a,1996b). [11] EachoftheseKhypothesescouldbetestedusingaTOST,butitisnotpossibletotestallKhypothesessimultaneouslybecauseanIUTdoesnotallowforthepossibilityofrejectingsomebutnotallofthehypotheses.Inaddition,becauseuptoKhypothesescouldbetrue,itisnecessarytohaveanadjustmentfortestingmultiplecomparisons.AnappropriateapproachistoconstructconfidenceintervalsforeachoftheseKhypotheses.Berger&Hsu(1996a)showthatiftheconfidenceinterval,constructedfromaTOST,isentirelycontainedintheequivalenceinterval[ΔL, ΔU],thetwomeansareequivalent.Theconfidenceintervalforthemultiplecomparisonscanbeconstructedfrom[5]and[6],whichgive whereSisestimatedfromthevarianceofε.Thesecanberearrangedtogivethefollowingconfidenceinterval [13] Torejectthenullhypothesis,theconfidenceintervalmustbeinsidetheequivalenceinterval.Notefirstthattheconfidenceintervalisconstructedwithtα,ν,andnotthestandardtα/2,ν.Second,becausetherearemultiplecomparisonstothesamecontrol,Dunnett′stshouldbeusedinsteadofStudent′stwithν=n+∑imi-(K+1) (Box3andsupportinginformation).Thisresultsinastrictlyconservativetest,andmoreaccuratep=0.05-leveltestsareavailableforbalanceddata(Giani&Straβburger,1994).Bonferronicorrectionsarenotappropriatebecausethetreatmentcomparisonsarecorrelatedbyusingthesamecontrol. Equivalencestandardsandtests Animportantissueforequivalencetestsisthedeterminationofequivalencestandards.Equivalencestandards, ΔLandΔU(orθLandθU),aredeterminedbyacombinationofregulatory,ecologicalandstatisticalconsiderations.Thestatisticalconsiderationsarerelatedtothesamplesizenecessarytoattainanacceptablepoweroftheequivalencetest.Forexample,totesttheequivalenceofproportions(equation[9]),asamplesizeof50providessuitablepowerforastandardof±20%,butthissamplesizeisinadequateforanequivalencestandardof±10%,whenasamplesize>150wouldbenecessary. Ecologicalandregulatoryconsiderationswilldeterminewhatisbiologicallyequivalentandsociallyacceptable.Ingeneral,thereisalargeclassofecologicalproblemsthathashardlybeenaddressedinappliedecology.Whenaretwoecologicalsystemsecologicallyequivalent?Howmuchchangecouldoccurtoanecologicalsystembeforeitshouldbeconsideredecologicallydifferent?Whataretheecologicallyessentialstructuralandfunctionalfeaturesofanecologicalsystem?Howmuchchangecananecologicalsystemtoleratebeforeitsessentialecologicalfeaturesareharmed?Howmuchcancomponentsofanecologicalsystemchangewithoutchangingtheecologicallyessentialfeaturesofthewholesysteminwhichtheyareembedded? Wedonotpresumetoanswerthesequestions,becauseitislikelythatconsiderableempiricalecologicalresearchwillbenecessarybeforemeaningfulanswerscanbeformulated.Thereexistformaltheoreticalconditionsunderwhichecologicalsystemsareequivalentornearlyso(Iwasaet al.,1987,1989),buttheseconditionsaresostrictandnarrowthattheycannotbereadilyimplemented,andempiricalcriteriaareneeded.Oneapproachforsettingecologicalequivalencestandardshasbeentousedatafromhistoricalteststhatcanberelatedtopotentiallysignificanteffects(Bertolettiet al.,2007;Phillipset al.,2001).Forexample,cladoceranshavebeenextensivelyusedtoevaluatethetoxicityofaquaticpollutants.Insomecases,thereareasufficientnumberoflaboratorytoxicitybioassaysthathavebeenassociatedwithpotentialecologicaleffectsthatitispossibletoestimatetheleveloftoxicitythatcouldcauseenvironmentalharm(Bertolettiet al.,2007).However,suchdatasetsareuncommon,sothisapproachisoflimitedapplicability.NosuchdatasetsexistforGMOecologicalriskassessment. Naturalvariabilityofthecontroltreatmenthasbeenoftenadvocatedasanapproachfordeterminingequivalencestandards(Barrettet al.,2015;EFSA,2010;Honget al.,2014;Kang&Vahl,2014;Vahl&Kang,2016;vanderVoetet al.,2011).Therationaleisthatifthecontrolhashighvariability,thenanytesttreatmentmustbemoredifferent,becausethehighvariabilityrequiresalargerequivalencestandard.Althoughthismaybetrueinfoodsafetyresearch,temporalandspatialcorrelationsinmanyecologicalfactorsmayresultinthecovarianceamongtreatmentandcontrolresponsesbeingasimportantasthevarianceincontrolresponse.Largepositivecovariancewouldimplythatthecontrolvarianceoverestimatestherelevantnaturalvariance,andleavesdoubtastohowtoestimatetherelevantnaturalvariance.Moreimportantly,thepotentialirreversibilityofecologicalchangemightarguefortighterequivalencestandards.Reversibilitymaybeassociatedwithecosystemresilience,whereasecologicalhysteresismaybeindicativeofirreversibility(Biggset al.,2009).Thus,itmaybemoreappropriatetodefineecologicalequivalencestandardsintermsofdegreeofconcern,namelytheminimumecologicaleffectthatissufficienttocauseharm(Perryet al.,2009). Thecriteriaforestablishingecologicalequivalencestandardsshouldcenterontheecologicalrisksthatsocietywantstoavoid(Andow,2011).Consequently,humanvalueswillbeanimportantconsiderationinestablishingecologicalequivalencestandards.Forexample,toconstructequivalencestandardstoevaluatetheeffectsofaGMcroponageneralistbiologicalcontrolagent,manyofthemostsignificantsocialvaluesareembeddedinthecrop/yieldlossrelationship.Asthecentralpurposeofbiologicalcontrolofcroppestsistominimizecropyieldloss,thevalueofbiologicalcontrolcanbemeasuredbythereductionincropyieldlossfrompests.Withaquantitativerelationshipbetweenthedensityofabiologicalcontrolagentandthesuppressionofthepestpopulation,thesetworelationshipscanbecombinedsothatachangeinnaturalenemydensitycanberelatedtoachangeincropyieldloss.Thiscombinedrelationshipcanbeusedtoestablishecologicalequivalencestandardsrelatedtoecologicalvalue(Andow,2011). Inferencesfromequivalencetests Toillustratehowequivalencetestscansupportbiosafetydecisions,weusetheexamplesinBox1-4.WhilethisdiscussionfocusesonGMObiosafety,itshouldbeclearthatwithotherexamples,thediscussioncanbegeneralizedtomanyareasofenvironmentalriskassessment.ManyresearchersstudyingGMOorBttoxicityhavebasedtheirconclusionsofbiosafetyonstandardhypothesistesting(e.g.,Lawoet al.,2009;Lundgren&Wiedenmann,2002;Meissle&Romeis,2009;Romeiset al.,2004;vonBurget al.,2010).Theseresearchersmakeclaimsforbiosafety,butinreality,theyhavecommittedthestatisticalerrorofacceptingthenullhypothesis,byconcludingthattherewerenoharmfuleffects.Here,wedemonstratehowtomakesoundinferencesof"noeffect"basedonequivalencetests.Wehavereanalyzedthedataofeightexamplestoillustratehowequivalencetestsdifferfromstandardhypothesistests(Table1).ThedatawereobtainedfromPaulaet al.(2016),Paula&Andow(2016)andGuoet al.(2008),andaredescribedindetailinBox1-4.Inalleightexamples,thestandardhypothesistestledtotheconclusionthataneffectoftheCrytoxinwasnotdetected(thestandardnullhypothesiswasnotrejected).Theequivalencetests,usingecologicallystrictequivalencestandardsof±20%,allowedustoconcludethatinsixoftheeightexamples,theeffectoftheCrytoxinwasequivalenttotheeffectofthecontrol.Theseresultsenableasoundconclusionof"noeffect"andsupportforabiosafetydeterminationoftheCrytoxinforHarmonia axyridisdevelopmenttime(Cry1F), Cycloneda sanguineadevelopmenttime(Cry1FandcombinedCry1AcandCry1F),andChrysopa pallensdevelopmenttime(GK12,NuCOTN99B,andamixture).Inotherwords,intheserespects,Crytoxinsare"safe"forH. axyridis, C. sanguineaandCh. pallens.ForC. sanguinea,thesamplesizesforthesetestswerequitemodest(n=8andn=10),whichshowsthatequivalencetestsdonotrequirelargesamplesizes.Theremainingtwocaseswerealsorevealing,astheywerestatisticallyindeterminate,neitherrejectingthenullhypothesisforthestandardtestorfortheequivalencetest.DevelopmenttimeofC. sanguineaonCry1Acwasnotequivalenttothecontrol,butthistreatmenthadasmallsamplesize(n=6),andmightbecomeequivalentwithhigherreplication.MortalityofBrevicoryne brassicaeonCry1Ac,hadap-valueof0.105underthestandardhypothesistest,withmortalityonCry1Acestimatedtobe31%comparedto19%onthecontroldiet.Inthiscase,increasedreplicationmightresultindetectionofasignificanteffectofCry1Acandadeterminationofnon-equivalence.Inanyevent,theequivalencetestreturnedtheaccurateresultthatmortalityofB. brassicaeonCry1Acwasnotequivalenttothecontrolandthistestdoesnotsupportabiosafetydecision.Equivalencetestsallowsoundinferenceaboutbiosafety,whilestandardhypothesistestsdonot. Burden of proof Finally, we note that equivalence statistics have direct and significant bearing on the debates about the burden of proof. Hobbs & Hilborn (2006) stated that the burden of proof has traditionally been on those who argued for regulatory intervention to stop pollution, i.e., pollution is allowed until its harms can be proven. Similarly, for invasive species risk assessment, the potential invader is assumed to be safe until proven to cause environmental harm (Simberloff,2005). Standard hypothesis testing is well-suited for these cases, as it can only establish whether there is a difference, whether there is environmental harm. However, this approach has allowed substantial pollution and the establishment of several harmful invasive species (Simberloff,2005), and as a general approach for environmental management, it has come under considerable criticism (e.g., Diamondetal.,2012; Hanson,2011; Kristofersson & Navrud,2005). In risk assessment, demonstration of biosafety is equally important as demonstration of harm. Equivalence tests are one way to establish a burden of proof of biosafety, by requiring demonstration of equivalence. However, equivalence tests are more flexible than this simple application of a "proof of safety" concept might imply. It is possible to consider the equivalence standard as a function of ecological value, and to test equivalence under different standards (ecological value). For example, a risk assessor could assess whether an environmental stressor is likely to reduce biological control of a pest thereby causing 5% more yield loss, i.e., using a 5% equivalence standard. An additional equivalence test could be performed to evaluate if the stressor is likely to be equivalent to the control at 2% or 1% yield loss levels (more stringent equivalence standards). The probability of equivalence will decline as the standard becomes smaller, so thep-values of the tests will increase (less likely to reject the null hypothesis that they are different). If thep-values of these three tests were respectively 0.02, 0.04, and 0.23, the analyst could conclude that if a 5% or 2% yield loss can be tolerated, the stressor and the control are equivalent with respect to their effects on biological control, but they are not equivalent if only 1% yield loss can be tolerated. When the magnitude of an insignificant risk can be differentiated from a significant risk, it will be possible to develop equivalence standards, and these can be used to establish a burden of proof of safety in ecological risk assessment. Equivalence tests can support a burden of proof of safety, and this shift does not necessarily create additional assessment costs. The cost of an equivalence test will depend primarily on the sample size and error variation, which depend primarily on the planned equivalence standard. A stricter equivalence standard will require a larger sample size and will have a higher cost than a test with a more lax equivalence standard. Because ecological systems often exhibit functional redundancy (Rosenfeld,2002), and some indirect species interactions attenuate as the pathway lengthens (Abramsetal.,1996), many functionally-based ecological equivalence standards may turn out to be lax. Andow (2011) suggested that an equivalence standard for a generalist biological control agent would probably be larger than the standard ±20%, and consequently, the cost of an equivalence test may be substantially lower than what is currently required under the standard hypothesis testing procedures. Acknowledgements: The USDA regional research project NC-205 to DAA and Rockefeller Resident Scholar in Bellagio Fellowships to DAA and GLL partially supported this work. Box 1.Equivalence test for two-sample, normal data The data originate from Paulaetal. (2016), who used an artificial tritrophic system to test if the toxin Cry1F, which occurs inBtmaize and cotton in Brazil, adversely affected an important biological control agent of agricultural pests, the coccinellid predatorHarmoniaaxyridis. This experiment measured the effect of Cry1F on larval development time of the predator. Aphid prey (Myzuspersicae) were allowed to feed for 24 h on a holidic diet in small cages with and without Cry1F at 20 μg·mL-1diet before being exposed to the predator. Neonate predator larvae were transferred daily into fresh cages to consume the aphids, and development time from neonate to pupa was recorded. Step 1.Specify equivalence standards. Values ofΔL=0.80 andΔU=1.25 were specified, which correspond to ±20% similarity. Step 2.Enter the data. LetX1, …,Xmdenote the untransformed development times (days) ofH.axyridisexposed to Cry1F viaM.persicae,m=39 (test treatment). LetC1, …,Cndenote development times of controlH.axyridis,n=30 (control treatment). In this example, under standard hypothesis testing, these were not significantly different. Step 3.Calculate test statistics as indicated in equation [6]. We have assumedσX2=σY2. IfσX2≠σY2, Welch′st-test with Welch-Satterthwaite degrees of freedom should be used, although there is no need to round the calculateddfs to an integer as sometimes recommended (USEPA,2010). Step 4.Conduct the TOST using equation [5]. For the example, the left tail of thet-distribution withα=0.05 andν=67 istα,ν=1.66792. Conclusion: Equivalence. The immature development time of the predator on the Cry1F treatment is equivalent to that in the control treatment. Box 2.Equivalence test for two-sample, binomial data The data originate from Paula & Andow (2016), who used an artificial holidic diet to test if theBttoxin Cry1Ac adversely affected an important non-target herbivore, the aphidBrevicorynebrassicae. This experiment measured the effect of Cry1Ac on the survival of reproductive apterous aphids during a three-day period. Five equal-sized apterous aphids were allowed to feed continuously on a holidic diet in small cages with and without Cry1Ac at 20 μg·mL-1diet. Twice daily, the number of dead aphids was counted, and the data record the total number that died during the experimental period and the number that survived. Step 1.Specify equivalence standards. HereΔL=-0.20 andΔU=0.20. Step 2.Enter contingency table data. Number of surviving and dead aphids that fed on a diet with 20 μg·mL-1Cry1Ac (testi) or control diet with no Cry1Ac. Under standard hypothesis testing, these were not significantly different (LRχ2=2.63, 1df,p=0.105). Step 4.Conduct the TOST using equation [11], with a critical value=3.841. In this case,zFM,L>3.841 andzFM,U<3.841. Conclusion: Nonequivalence. The lower one-sided test is rejected, but the upper one-sided test is not rejected. Therefore the two treatments are not equivalent. The survival rate of the aphid feeding on Cry1Ac was not equivalent to the control. Box 3.Equivalence test for multiple-sample, normal data The data originate from Paulaetal. (2016), who used an artificial tritrophic system to test if theBttoxins Cry1Ac alone, Cry1F alone, or Cry1Ac/Cry1F together adversely affected an important biological control agent, the coccinellid predatorCyclonedasanguinea. This experiment measured the effect on larval development time of the predator from neonate to pupa, and was designed to test if the two toxins interacted with synergistic effects. Aphid prey (Myzuspersicae) were allowed to feed for 24 hours before predator exposure on a holidic diet in small cages with and without Cry1Ac or Cry1F or both together. Neonate predator larvae were transferred daily into fresh cages to consume the aphids. Step 1.Specify equivalence standards. Values ofΔL=0.80 andΔU=1.25 were specified, which correspond to ±20% similarity. Step 2.Enter data. LetX1i, …,Xmidenote the untransformed measurements on themilarvae in theithtest treatment andC1, …,Cndenote the untransformed measurements on thenlarvae in the control treatment. The data are larval development times ofC.sanguineareared onM.persicaeaphids that fed on an artificial diet with 20 μg·mL-1Cry1Ac (Test 1), 20 μg·mL-1Cry1F (Test 2), or both 20 μg·mL-1Cry1Ac and 20 μg·mL-1Cry1F (Test 3). The control treatment was a control diet with no Cry toxin. There were three test treatments, soK=3, withm1=6,m2=7,m3=12, andn=19. In this example, under standard hypothesis testing, none of the test treatments were significantly different from the control and there was no interaction of the two toxins. Step 3.Calculate test statistics [13] and find the appropriate value for the one-tailed Dunnett′st, based onν,Kandα. The critical value for Dunnett′stwas calculated forν=41df,K=3 comparisons, andα=0.05, using SAS (see below). The critical value is 2.16217. We can also determine if Test 3 is equivalent to Test 1 and Test 2, which evaluates the hypothesis that there is no interaction between the two toxins (all calculations are not shown). Step 4.Compare the lower and upper confidence intervals,CILandCIU, with the equivalence interval (0.80, 1.25). If theCIs are entirely within the equivalence interval (0.80, 1.25), then the test treatment mean is equivalent to the control treatment. Conclusions: (1) Test 1 is not equivalent to the control, while Test 2 and Test 3 are equivalent to the control. The development time of the predator feeding on aphids exposed to Cry1Ac was not equivalent to the control, while for the Cry1F and the combination of both toxins, they were equivalent. (2) Both Test 1 and Test 2 are not equivalent to Test 3, which implies that the hypothesis of no interaction cannot be rejected, i.e., there might be an interaction. Calculation of critical value,x, for one-sided Dunnett′stusing SAS: data; array lambda{3}; ∥lambda{i}=sqrt (mi/(mi+n)) x=probmc ("dunnett1", ., 0.95, 41, 3, of lambda 1-lambda 3); Box 4.Equivalence test for multiple-sample, normal data with replicated experiments The data originate from Guoetal. (2008), who used a plant-based laboratory tritrophic system to test if larval development time (neonate to pupa) of an important biological control agent,Chrysopapallens, differed when feeding on aphids from the cotton varieties Simian 3 (control), GK12 (with Cry1Ab/Ary1Ac fusion protein), NuCOTN 99B (Cry1Ac), or alternately feeding on aphids from the three varieties. Aphid prey (Aphisgossypii) were collected on excised leaves from field plants and given to individual predators in petri dishes. Fresh aphids were supplied daily. Step 1.Specify equivalence standards. Values ofΔL=0.80 andΔU=1.25 were specified, which correspond to ±20% similarity. Step 2.Enter data. LetX1ir, …,Xmirdenote the untransformed measurements on themirlarvae in theithtest treatment andrthexperimental replicate, andC1r, …,Cnrdenote the untransformed measurements on thenrlarvae in therthexperimental replicate for the control treatment. The data are larval development times (days) ofC.pallensreared onM.persicaeaphids that fed on cotton variety GK12 (Test 1), NCOTN 99B (Test 2), or an alternating mixture of aphids (Test 3). The control treatment was the non-Btvariety Simian 3. There were three test treatments (K=3) and three replications of the experiment (R=3) withm1r=19, 17, and 18,m2r=18, 18, 17,m3r=18, 17, 18, andnr=19, 19, 18. In this example, under standard hypothesis testing, none of the test treatments were significantly different from the control, as indicated in the ANOVA table. Step 3.Calculate test statistics [13] and find the appropriate value for the one-tailed Dunnett′st, based onν,Kandα, as in Box 3. The critical value for Dunnett′stwas calculated forν=204df,K=3 comparisons, andα=0.05. The critical value is 2.07698. Step 4.Compare the lower and upper confidence intervals,CILandCIU, with the equivalence interval (0.80, 1.25). If theCIs are entirely within the equivalence interval (0.80, 1.25), then the test treatment mean is equivalent to the control treatment. Conclusion: Equivalence. All three Test treatments are equivalent to the control. The larval development time of the predator feeding on aphids exposed to Cry toxins inBtcotton plants was equivalent to the control plant. References Abrams P A, Menge B A, Mittelbach G G, Spiller D A and Yodzis P, 1996. The role of indirect effects in food webs∥Polis G A and Winemiller K O.FoodWebs:IntegrationofPatterns&Dynamics. New York: Springer: 371-395. Agresti A, 1996.AnIntroductiontoCategoricalDataAnalysis. New York, NY: Wiley. Andow D A, 2011. Assessing unintended effects of GM plants on biological species.JournalfürVerbraucherschutzundLebensmittelsicherheit, 6(S1): 119-124. Barrett T J, Hille K A, Sharpe R L, Harris K M, Machtans H M and Chapman P M, 2015. Quantifying natural variability as a method to detect environmental change: definitions of the normal range for a single observation and the mean of M observations.EnvironmentalToxicologyandChemistry, 34: 1185-1195. Berger R L, 1982. Multiparameter hypothesis testing and acceptance sampling.Technometrics, 24: 295-300. Berger R L and Hsu J C, 1996a. Bioequivalence trials, intersection-union tests and equivalence confidence sets.StatisticalScience, 11: 283-303. Berger R L and Hsu J C, 1996b. Rejoinder: bioequivalence trials, intersection-union tests and equivalence confidence sets.StatisticalScience, 11: 315-319. Bertoletti E, Buratini S V, Prósperi V A, Araújo R P A and Werner L I, 2007. Selection of relevant effect levels for using bioequivalence hypothesis testing.JournaloftheBrazilianSocietyofEcotoxicology, 2: 139-145. Biggs R, Carpenter S R and Brock W A, 2009. Turning back from the brink: detecting an impending regime shift in time to avert it.ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica, 106: 826-831. Brosi B J and Biber E G, 2009. Statistical inference, Type Ⅱ error, and decision making under the US Endangered Species Act.FrontiersinEcologyandtheEnvironment, 7: 487-494. Chen J J, Tsong Y and Kang S H, 2000. Tests for equivalence or noninferiority between two proportions.TherapeuticInnovation&RegulatoryScience, 34: 569-578. Diamond J, Denton D, Anderson B and Phillips B, 2012. It is time for changes in the analysis of whole effluenttoxicity data.IntegratedEnvironmentalAssessmentandManagement, 8: 351-358. EFSA (European Food Safety Authority), 2010. Scientific opinion on statistical considerations for the safety evaluation of GMOs.EFSAJournal, 8(1): 1250. Farrington CP and Manning G, 1990. Test statistics and sample size formulae for comparative binomial trials with null hypothesis of non-zero risk difference or non-unity relative risk.StatisticsinMedicine, 9: 1447-1454. Giani G and Straβburger K, 1994. Testing and selecting for equivalence with respect to a control.JournaloftheAmericanStatisticalAssociation, 89: 320-329. Guo J Y, Wan F H, Dong L, Lövei G L and Han Z J, 2008. Tri-trophic interactions betweenBtcotton, the herbivoreAphisgossypiiGlover (Homoptera: Aphididae), and the predatorChrysopapallens(Rambur) (Neuroptera: Chrysopidae).EnvironmentalEntomology, 37: 263-270. Hanson N, 2011. Using biological data from field studies with multiple reference sites as a basis for environmental management: the risks for false positives and false negatives.JournalofEnvironmentalManagement, 92: 610-619. Hobbs N T and Hilborn R, 2006. Alternatives to statistical hypothesis testing in ecology: a guide to self-teaching.EcologicalApplications, 16: 5-19. Hoenig J M and Heisley D M, 2001. The abuse of power: the pervasive fallacy of power calculations for data analysis.AmericanStatistician, 55: 19-24. Hong B, Fisher T L, Sult T S, Maxwell C A, Mickelson J A, Kishino H and Locke M E H, 2014. Model-based tolerance intervals derived from cumulative historical composition data: application for substantial equivalence assessment of a genetically modified crop.JournalofAgriculturalandFoodChemistry, 62: 9916-9926. Iwasa Y, Andreasen V and Levin S A, 1987. Aggregation in model ecosystems. I. Perfect aggregation.EcologicalModelling, 37(3-4): 287-302. Iwasa Y, Levin S A and Andreasen V, 1989. Aggregation in model ecosystems II. Approximate aggregation.MathematicalMedicineandBiology, 6: 1-23. Kang Q and Vahl C I, 2014. Statistical analysis in the safety evaluation of genetically-modified crops: equivalence tests.CropScience, 54: 2183-2200. Kristofersson D and Navrud S, 2005. Validity tests of benefit transfer — are we performing the wrong tests?EnvironmentalandResourceEconomics, 30: 279-286. Lawo N C, Wäckers F L and Romeis J, 2009. IndianBtcotton varieties do not affect the performance of cotton aphids.PLoSONE, 4(3): e4804. Liu J P and Chow S C, 1996. Comment: Bioequivalence trials, intersection-union tests and equivalence confidence sets.StatisticalScience, 11: 306-312. Lundgren J G and Wiedenmann R N, 2002. Coleopteran-specific Cry3Bb toxin from transgenic corn pollen does not affect the fitness of a non-target species,ColeomegillamaculataDeGeer (Coleoptera: Coccinellidae).EnvironmentalEntomology, 31: 1213-1218. Meissle M and Romeis J, 2009. The web-building spiderTheridionimpressum(Araneae: Theridiidae) is not adversely affected byBtmaize resistant to corn rootworms.PlantBiotechnologyJournal, 7: 645-656. Nakagawa S and Foster T M, 2004. The case against retrospective statistical power analyses with an introduction to power analysis.ActaEthologica, 7: 103-108. Patterson S D and Jones B, 2005.BioequivalenceandStatisticsinClinicalPharmacology. Boca Raton, USA: Chapman & Hall/CRC. Paula D P and Andow D A, 2016. Differential Cry toxin detection and effect onBrevicorynebrassicaeandMyzuspersicae(Hemiptera: Aphidinae) feeding on artificial diet.EntomologiaExperimentalisetApplicata, 159: 54-60. Paula D P, Andow D A, Bellinati A, TimbR V, Souza L M, Pires C S S and Sujii E R, 2016. Limitations in dose-response and surrogate species methodologies for risk assessment of Cry toxins on arthropod natural enemies.Ecotoxicology, 25: 601-607. Perry J N, ter Braak C J F, Dixon P M, Duan J J, Hails R S, Huesken A, Lavielle M, Marvier M, Scardi M, Schmidt K, Tothmeresz B, Schaarschmidt F and van der Voet H, 2009. Statistical aspects of environmental risk assessment of GM plants for effects on non-target organisms.EnvironmentalBiosafetyResearch, 8: 65-78. Phillips B M, Hunt J W, Anderson B S, Puckett H M, Fairey R, Wilson C J and Tjeerdema R, 2001. Statistical significance of sediment toxicity test results: threshold values derived by the detectable significance approach.EnvironmentalToxicologyandChemistry, 20: 371-373. Raybould A, 2010. Reducing uncertainty in regulatory decision-making for transgenic crops: more ecological research or clearer environmental risk assessment?GMCrops, 1: 25-31. Romeis J, Dutton A and Bigler F, 2004.Bacillusthuringiensistoxin (Cry1Ab) has no direct effect on larvae of the green lacewingChrysoperlacarnea(Stephens) (Neuroptera: Chrysopidae).JournalofInsectPhysiology, 50: 175-183. Romeis J, Hellmich R L, Candolfi M P, Carstens K, De Schrijver A, Gatehouse A M R, Herman R A, Huesing J E, McLean M A, Raybould A, Shelton A M and Waggoner A, 2011. Recommendations for the design of laboratory studies on non-target arthropods for risk assessment of genetically engineered plants.TransgenicResearch, 20: 1-22. Rosenfeld J S, 2002. Functional redundancy in ecology and conservation.Oikos, 98: 156-162. Sasabuchi S, 1980. A test of a multivariate normal mean with composite hypotheses determined by linear inequalities.Biometrika, 67: 429-439. Schuirmann D J, 1987. A comparison of the two one-sided tests procedure and the power approach for assessing the equivalence of average bioavailability.JournalofPharmacokineticsandBiopharmaceutics, 15: 657-680. Simberloff D, 2005. The politics of assessing risk for biological invasions: the USA as a case study.TrendsinEcologyandEvolution, 20: 216-222. Suter G W I I, 2006.EcologicalRiskAssessment. 2 ed. Boca Raton, FL: CRC Press. USEPA, 2010.NationalPollutantDischargeEliminationSystemTestofSignificantToxicityImplementationDocument:AnAdditionalWholeEffluentToxicityStatisticalApproachforAnalyzingAcuteandChronicTestData.EPA833-R-10-003. Washington, DC: USEPA. Vahl C I and Kang Q, 2016. Equivalence criteria for the safety evaluation of a genetically modified crop: a statistical perspective.TheJournalofAgriculturalScience, 154: 383-406. van der Voet H, Perry J N, Amzal B and Paoletti C, 2011. A statistical assessment of differences and equivalences between genetically modified and reference plant varieties.BMCBiotechnology, 11: 15. von Burg S, Müller C B and Romeis J, 2010. Transgenic disease-resistant wheat does not affect the clonal performance of the aphidMetopolophiumdirhodumWalker.BasicandAppliedEcology, 11: 257-263. Westlake W J, 1981. Response to T.B.L. Kirkwood: bioequivalence testing — a need to rethink.Biometrics, 37: 589-594. (责任编辑:杨郁霞) 收稿日期(Received):2015-12-15接受日期(Accepted): 2016-02-29 *通讯作者(Author for correspondence), E-mail: dandow@umn.edu DOI:10. 3969/j.issn.2095-1787.2016.02.002