基于GA-GRNN的瓦斯涌出量预测

崔义强　赵顺利

(1.武汉钢铁集团开圣科技有限责任公司; 2.武汉理工大学资源与环境工程学院)



基于GA-GRNN的瓦斯涌出量预测

崔义强1赵顺利2

(1.武汉钢铁集团开圣科技有限责任公司; 2.武汉理工大学资源与环境工程学院)

摘要为防治煤矿瓦斯灾害，将遗传算法和广义回归神经网络结合起来，构建出GA-GRNN方法，利用遗传算法的全局寻优和广义回归神经网络结构简单的特点，自动搜索和匹配最优光滑因子参数，实现瓦斯涌出量的高精度预测。通过与实际工程中瓦斯涌出量预测比较，表明GA-GRNN法在实现高精度预测的同时，能够有效避免训练数据预测精度的降低。

关键词瓦斯涌出量GA-GRNN遗传算法广义回归神经网络

瓦斯灾害作为煤矿最重要的灾害之一，给矿井的安全生产带来极大的威胁。随着国内煤矿安全形势的好转，瓦斯事故造成的事故量与死亡人数得到了较好地控制，但依旧时有发生。针对煤矿瓦斯事故的防治，各产煤国都建立了专门的研究机构对其进行研究。随着研究的深入，瓦斯涌出量预测作为一个研究方向备受关注，从单因素预测向多因素预测方向发展。相关学者也引入了诸如神经网络、支持向量机、灰色系统理论等智能算法[1-3]，但是单个智能算法在解决瓦斯涌出量预测问题时，往往表现出较大的局限性，因此一些耦合算法也相继被提出[4-6]。

目前，瓦斯涌出量预测研究已取得较好的成果，对工程实际起到了一定的指导作用。但是部分瓦斯涌出量研究中，存在过度重视预测数据的准确度，而造成训练数据精度减小的问题，此类算法以BP神经网络为代表。而且相关的智能算法在应用过程中，也存在有参数选取的问题，部分智能算法的参数需要人工调试，无法实现与实际问题的自动匹配，影响了具体应用。

1GA-GRNN理论

1.1遗传算法

遗传算法(GA)由J.Hollnad[7]于1975年提出，通过模拟自然界的生物进化，进而实现全局搜索和全局优化。在求解实际复杂问题时，遗传算法不局限于特定的研究领域，因此得到广泛应用。

遗传算法是一种兼容性强的搜索方法，能对整个搜索空间实现自动获取，主要模拟自然界生物在进化过程中的复制、交叉和变异现象。在进化过程中，物种的发展趋向于更好的方向，即优胜劣汰的进化规律，最终留下的是适应环境生存的最好种群。与传统搜索方法相比，遗传算法具有寻优速度快、通用性好、搜索效率高、系统健壮性强、搜索范围广范、能和其他算法相融合等优点，使其具有很高的应用价值。遗传算法原理如图1所示。

图1　遗传算法原理

更一般的基本遗传算法的形式化定义可用式(1)表示:

(1)

式中,C为个体编码方法；E为个体适应度评价函数；P0为初始种群；M为群体大小；Φ为选择算子；Γ为交叉算子；ψ为变异算子；T为遗传运算终止条件。

1.2广义回归神经网络

企业需提升对物流人才培训的重视程度，将人才激励机制制定出来并促使其逐步完善，对企业中全体员工的物流成本意识予以强化。与此同时，企业还需将有效的物资采购成本控制体系构建起来，通过对价值的合理分析来选择更加优质、价廉的物资，降低企业的采购成本，实施全面成本管理，将物流成本管理组织体系建立起来，加大对全面成本管理的宣传力度，提升企业员工参与成本管理的积极性，明确物流成本管理于企业全面成本管理中的地位，对综合控制展开系统分析，全面实现供应链一体化目标，将物流成本综合管理框架建立起来，提升企业在市场当中的竞争力。

径向基函数神经网络有几种比较重要的变形，其中之一就是广义回归神经网络(GRNN)。广义回归神经网络由美国学者Donald F. Specht于1991年提出，理论基础为非线性回归[8]，在训练样本少时，也能取得较好的回归效果。GRNN具有很强的非线性映射能力和柔性网络结构以及高度的容错性和鲁棒性，适用于解决非线性问题，在不同的研究领域得到了广泛应用。

广义回归神经网络分为输入层、模式层、求和层以及输出层四层，具体结构如图2所示。

广义回归神经网络结构固定，不需要做过多的假设，以输入矩阵X和输出矩阵Y为例，说明广义回归神经网络的理论基础。输入层功能较为简单，即直接将输入变量传递给模式层，模式层神经元的数目与学习样本数目N相等。模式层神经元传递

图2　广义回归神经网络结构

函数一般取高斯函数：

(2)

式中，X为网络输入矩阵，Xi为第i个神经元对应的学习样本；σ为网络光滑因子。

通过模式层得到一组向量，代入到求和层，求和层中对两种类型的神经元求和：

(3)

(4)

式(3)是对模式层的输出进行算术求和，式(4)是对模式层的输出加权求和。

输出层的维数等于输出向量的维数m，输出结果计算如下：

(5)

广义回归神经网络的理论基础是非线性回归分析，参数σ为高斯函数的宽度系数，在此称为光滑因子。当光滑因子较大时，广义回归神经网络的拟合曲线非常平滑，但是相应的误差也较大;当光滑因子趋近于0时，网络的泛化能力会非常差，预测效果会非常差，所以选择一个合适的光滑因子至关重要。

1.3GA-GRNN构建

对于广义回归神经网络而言，光滑因子的选择直接影响网络的性能。传统的广义回归神经网络无法自动匹配最优的光滑因子，也无较好的算法确定光滑因子，因此需要手动调节，经过数次验算确定较好的取值。因无法自动匹配最优的光滑因子参数，限制了广义回归神经网络的应用。为此，引入遗传算法，对光滑因子可能的取值进行全局搜索，自动搜索最优光滑因子参数值。通过把遗传算法和广义回归神经网络结合到一起，构建出GA-GRNN方法。构建流程如下：

(1)建立光滑因子可能取值搜索范围，在此范围内建立光滑因子的初始种群，并设定遗传算法所需的遗传概率、交叉概率、变异概率和进化代数等参数。针对实际问题时，遗传算法上述参数值的设置并不需要过分严格，一般情况下均可取得较满意的优化效果。

(2)建立遗传算法的适应度函数。本文采用的适应度函数为预测值的精度，即广义回归神经网络的预测值与实际值误差的绝对值之和，作为评价种群中个体的适应度函数。适应度取值越小，表明该个体越优良。

(3)当最佳个体适应度和整个种群的平均适应度趋于不变时，可认为遗传算法得到了较好的优化效果。把最佳个体的值赋予光滑因子，并代入广义回归神经网络中，进行实际预测。

(4)当第三步不能达到理想效果时，可适当增加遗传算法的搜索范围和进化代数。

2工程实例

为进一步验证基于遗传算法优化的广义回归神经网络(GA-GRNN)在瓦斯涌出量预测中的有效性，选取18组实际工程数据进行训练预测，具体数据见表1。根据实际情况，瓦斯涌出量的影响因素分别为煤层瓦斯含量、煤层厚度、采出率、开采强度。

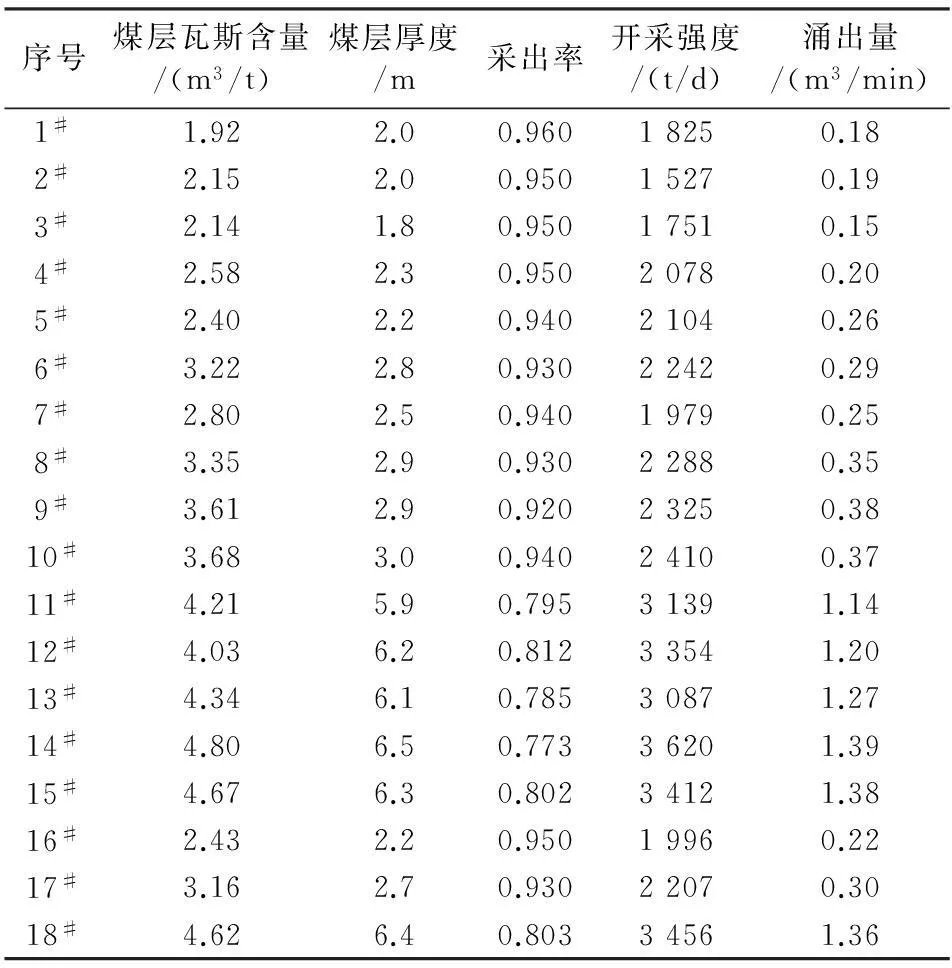
表1　瓦斯涌出量[9]

为了与文献[9]中的预测结果做对比，采取与原文献相同的训练数据和预测数据分组，即前15组作为训练数据，后3组作为预测数据。广义回归神经网络的参数主要是光滑因子，利用遗传算法建立光滑因子的种群，种群规模为50，进化代数为100代。选择概率、交叉概率和变异概率分别为0.3，0.6，0.1。光滑因子的搜索范围为[0 ，1 000]。通过模拟得到遗传算法的适应度曲线，如图3所示。通过图3可以发现，适应度在进化到100代时已基本上不再变化，搜索到的光滑因子达到了较好的取值，为188.5。

图3　遗传算法适应度曲线

把最优光滑因子参数代入广义回归神经网络中，得到后3组预测值见表2。为了方便与BP神经网络比较，文献[9]采用BP神经网络的预测效果同样列于表2中。通过表2可以看出，GA-GRNN的预测精度与文献[9]中采用方法的预测精度相当。具体表现在16#和17#数据GA-GRNN的预测精度略低于BP神经网络，18#数据GA-GRNN的预测精度明显优于BP神经网络;GA-GRNN相对误差的平均值为3.70%，略优于BP的3.76%。仅通过预测数据来看，GA-GRNN的预测精度较高，与BP神经网络相当。

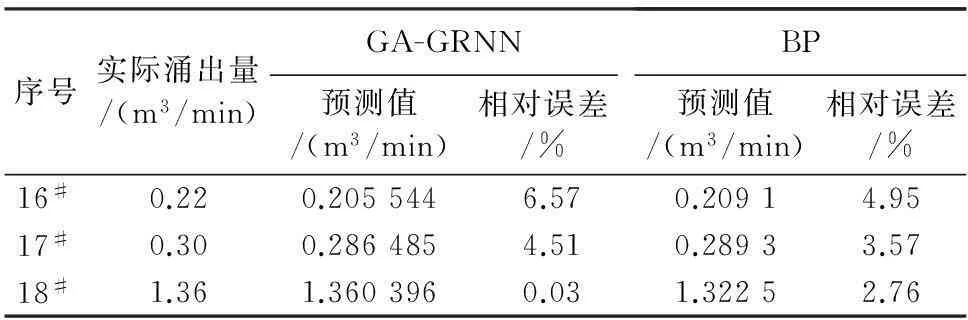
表2　预测效果对比

虽然BP神经网络也能得到较为满意的预测精度，但是从过程来看，BP神经网络确定网络结构较为复杂，且参数较多，不易实现参数自动匹配；BP神经网络容易陷入局部极小值，要通过多次训练才能找到较为合适的网络结构及参数；在与其他智能算法结合时，BP神经网络的参数多且网络复杂，会大大增加计算机运算时间；BP神经网络进行训练过程中会存在有欠学习和过学习现象，造成预测数据精度和训练数据精度不能同时保证。为了进一步对比GA-GRNN算法和BP神经网络，把18组试验数据全部代入训练好的网络中进行回判，如图4所示。

通过图3可以发现，BP神经网络虽然预测数据的预测精度较好，但是训练数据的预测精度误差很大，最大误差达到了25%；GA-GRNN对于训练数据的预测精度是极高的，明显优于BP神经网络。

3结论

将遗传算法和广义回归神经网

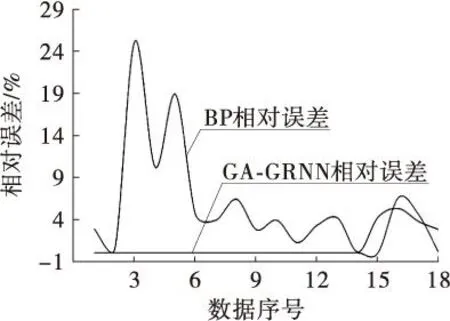
图4　预测精度对比

络结合起来，提出了GA-GRNN的方法，实现了广义回归神经网络光滑因子确定的难题和网络参数的自动匹配。通过GA-GRNN在工程实例中的验证，训练数据和预测数据的预测精度较高，得到以下结论：

(1)GA-GRNN可以实现广义回归神经网络参数的自动匹配，在瓦斯涌出量预测时可实现了高精度预测，最大误差为6.57%。

(2)相较于BP神经网络，GA-GRNN不易陷入局部极小值，同时避免了过学习和欠学习的问题。进行瓦斯涌出量预测时，训练数据和预测数据的预测精度都得到了保证。

(3)单独的预测数据的预测精度并不能评价一个智能算法的优劣。在瓦斯涌出量预测时，BP神经

网络预测数据的预测精度也较高，但是由于自身存在的一些缺陷，限制了在工程中的应用。

参考文献

[1]王轶波,徐阿猛,齐黎明,等.基于Matlab的神经网络工具箱在矿井瓦斯治理中的应用[J].煤矿安全,2010(3):20-23.

[2]黄为勇,童敏明,任子晖.基于SVM的瓦斯涌出量非线性组合预测方法[J].中国矿业大学学报,2009,38(2):234-239.

[3]伍爱友,田云丽,宋译,等.灰色系统理论在矿井瓦斯涌出量预测中的应用[J].煤炭学报,2005,30(5):589-592.

[4]韩义波.基于GA-ELM的瓦斯涌出量预测[J].煤矿安全,2015,46(4):166-169.

[5]撒占友,綦鲁杰,刘岩.基于PCA-FOA-GRNN的回采工作面瓦斯涌出量预测[J].煤矿安全,2015,46(1):133-136.

[6]付华,姜伟,单欣欣.基于耦合算法的煤矿瓦斯涌出量预测模型研究[J].煤炭学报,2012,37(4):654-658.

[7]Holland J H. OutlineofralogicaltheoyrofadaPtivesystems[J].Journal of the Association for Computing Machinery,1962,9(3):297-314.

[8]Specht D F, Shapiro P D. Generalization accuracy of probabilistic neural networks compared with backpropagation networks[C]∥Singapore:The International Joint Conference on Neural Networks, 1991:887-892.

[9]朱红青，常文杰，张彬.回采工作面瓦斯涌出BP神经网络分源预测模型及应用[J].煤炭学报,2007,32(5):504-508.

(收稿日期2015-09-28)

Prediction of the Gas Emission Quantity Based on GA-GRNN

Cui Yiqiang1Zhao Shunli2

(1. Kaisheng Science Co. Ltd., Wuhan Iron and Steel (Group); 2. School of Resources and Environmental Engineering, Wuhan University of Technology)

AbstractIn order to prevent the coal mine gas disaster and achieve the high precision prediction of gas emission quantity, the genetic algorithm and the generalized regression neural network are combined to construct the GA-GRNN model. Based on the advantages of global optimization of the characteristics of genetic algorithm and the simple structure of the generalized regression neural network to search and match the optimal smoothing factors to achieve high precision prediction of gas emission quantity.Comparison the prediction results with the gas emission quantity in practical engineering is conducted,the results show that the high precision results can be obtained by the GA-GRNN model,besides that the prediction precision of the training data can be avoided decreasing.

KeywordsGas emission quantity, GA-GRNN, Genetic algorithm, Generalized regression neural network

崔义强(1982—)，男，经理助理，工程师，430063湖北省武汉市东湖高新区光谷大道。