掌握方法 灵活解方程

赵正祥



掌握方法灵活解方程

赵正祥

解分式方程的基本数学思想就是转化，将其转化为整式方程，其基本解题方法是通过去分母将分式方程转化为整式方程.与解一元一次方程类似，一般步聚是：（1）去分母，把分式方程化为整式方程；（2）解这个整式方程；（3）检验；（4）写出结论.解答时，需要我们根据方程整体特点，灵活应用解题方法解方程.现以2015年中考试题为例加以说明.

【分析】直接应用转化思想，使其转化为整式方程进行求解；也可以先观察所给的方程，不难发现方程左边两个分式的分母互为相反数，不妨先考虑它们的分母，通过变形化成相同的分母，再进行整体加减运算，然后解方程进行求解.

解：方法一：方程两边同乘（x-3），得：

（2-x）-1=x-3，

解这个方程，得：

x=2.

检验：当x=2时，x-3≠0.

所以，x=2是原方程的解.

方程两边同乘（x-3），得：

1-x=x-3，

解这个方程，得：

x=2，

检验：当x=2时，x-3≠0，

所以，x=2是原方程的解.

【点悟】本题方法二根据方程中分式的分母具有互为相反数的整体特征，灵活将它们变形转化为相同的分母，再进行整理、合并，求得方程的解.

【分析】根据解分式方程的一般步骤，可以直接在方程两边同时乘最简公分母，使其转化为关于x的一元一次方程进行解答，也可以对其进行适当变形，灵活根据分式的相关性质确定方程的解

解：方法一：方程两边同乘x（x-3），得：

2x=3（x-3），

解这个方程，得：

x=9.

检验：当x=9时，x（x-3）≠0.

所以，x=9是原方程的解.

方法二：原方程变形为

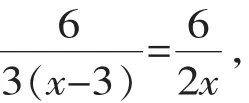
根据分式值相等的意义，可得：

3（x-3）=2x，

解这个方程，得：

x=9.

检验：当x=9时，x（x-3）≠0.

所以，x=9是原方程的解.

方法三：原方程变形为：

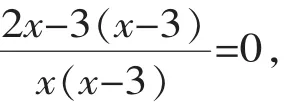
根据分式值为0的意义，可得：

2x-3（x-3）=0，

解这个方程，得：

x=9.

检验：当x=9时，x（x-3）≠0.

所以，x=9是原方程的解.

【点悟】本题是一道较为简单的分式方程，上述解法能够根据方程的整体特征，从不同的思考角度恰当地应用不同的方法解分式方程，并对所求得的方程解进行检验.

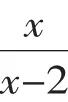
解：方法一：原方程变为：

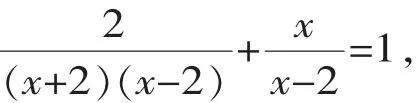
去分母得：2+x（x+2）=x2-4，

去括号，得2+x2+2x=x2-4，

解得x=-3，

检验：当x=-3时，（x+2）（x-2）≠0，

所以，x=-3是原方程的根.

方法二：原方程变形为

去分母得：2+2（x+2）=0，

去括号，得2+2x+4=0，

解得x=-3，

检验：当x=-3时，（x+2）（x-2）≠0，

所以，x=-3是原方程的根.

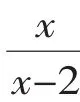
（作者单位：江苏省建湖县汇文实验初中教育集团汇文校区）