《分式》测试题参考答案



《分式》测试题参考答案

1. C提示：由题意可知x- 2=0，得x=2.由x+1≠0，得x≠- 1，所以x=2.

2. D提示：由题意可知x- 2是分式的分母，因此x- 2≠0，所以x≠2.

3. C提示：选项A中是异分母分式相加，要先通分，再相加；选项B中的分式不能约分；选项C，先将分式的分母分解因式，再进行约分，是正确的；选项D，分式本身、分子与分母中的两项符号，同时改变才能确保分式的值不变.

4. C提示：先通分使异分母分式转化为同分母分式，再相加并约分化成最简分式.

5. B提示：将方程两边同时乘x（x-2）得：3（x- 2）=2x，解得x=6.检验：当x=6时，x（x- 2）=24≠0，因此，x=6是原分式方程的解.

9. x≠- 3提示：当分母不为0时，分式有意义，即x+3≠0.

11. x（x+3）（x- 3）提示：将这两个分式的分母先分别因式分解，再确定最简公分母.

13. x+y提示：根据分式的乘法法则直接进行计算.

19.∵当x=- 1时，分式的值为零，∴x+y=0，则y=1，∴x- 2y=- 3.

（2）解得x=-2，检验：当x=-2时，2（x-2）≠0，所以x=-2是原方程的解.

（1）当x=3时，原式=2；

∵x≠- 1且x≠0且x≠1，∴当x=2时，原式=0；当x=- 2时，原式=8.

24.∵m是方程x2+3x- 1=0的根，∴m2+3m- 1=0，即m2+3m=1，

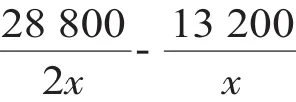
（2）设每件衬衫的标价至少是a元，由（1）得第一批的进价为：13200÷120=110（元/件），第二批的进价为：120（元/件），由题意可得：120（a- 110）+（240- 50）（a- 120）+50（0.8a- 120）≥25%×42 000.解得a≥150，即每件衬衫的标价至少是150元.答：第一批衬衫为120件.每件衬衫的标价至少为150元.