中心对称 贯穿始终
2016-06-01李建华
李建华
中心对称贯穿始终
李建华
本章以中心对称为主线,从探究图形旋转的性质,过渡到中心对称与中心对称图形,进而到中心对称图案的设计;接着研究属于中心对称的四边形——平行四边形及特殊的平行四边形(矩形、菱形、正方形)的概念、性质及判定;最后从中心对称的角度研究了三角形中位线的性质.从生活到实践,从实践到探索,从探索到发现,从发现到归纳,再把归纳得到的结论用来解决问题.
一、图形旋转的性质
例1如图1,在正方形网格中有△ABC,△ABC绕O点按逆时针方向旋转90°后的图案应该是().

图1
【解析】根据图形旋转的性质:“一个图形和它经过旋转得到的图形中,对应点到旋转中心的距离相等,两组对应点分别与旋转中心连线所成的角相等.”分别找到点A、B、C绕O点按逆时针方向旋转90°后的对应点,从而选择A.
二、中心对称与中心对称图形
例2(1)(2015·甘孜)如图2,下列图形中,是中心对称图形的为().
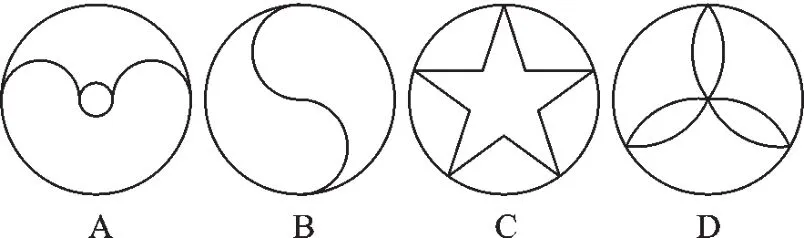
图2
(2)如图3,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是().

图3
A.(3,-1)B.(0,0)
C.(2,-1)D.(-1,3)
【解析】(1)本题考查了中心对称图形的概念,要注意与轴对称图形概念的区别.识别轴对称图形的关键是寻找对称轴,图形沿对称轴折叠后两部分可重合;识别中心对称图形是要寻找对称中心,绕对称中心旋转180°后与原图形重合.答案:B.
(2)本题考查了中心对称的性质:对称点的连线经过对称中心,且被对称中心平分.确定E点位置是关键.连接对称点AA1、CC1,因为对称点的连线经过对称中心,则AA1与CC1的交点就是对称中心E点,在坐标系内确定出其坐标.答案:(3,-1).
三、平行四边形与矩形、菱形、正方形
例3(1)(2015·福建)如图4,在▱ABCD中,O是对角线AC、BD的交点,下列结论错误的是().
A. AB∥CD B. AB=CD
C. AC=BD D. OA=OC
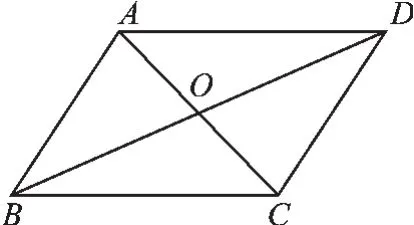
图4

图5
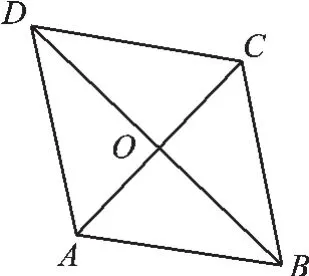
图6
(2)(2015·益阳)如图5,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是().
A.∠ABC=90°B. AC=BD
C. OA=OB D. OA=AD
(3)如图6,在菱形ABCD中,下列结论错误的是().
A. BO=DO
B.∠DAC=∠BAC
C. AC⊥BD
D. AO=DO
(4)在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是().
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量对角线是否相等
D.测量其中三个角是否都为直角
【解析】本题考查了平行四边形与矩形、菱形的性质及判定,理解并熟记性质及判定定理是解题的关键.平行四边形的对边相等、对角相等、对角线互相平分;矩形的四个角都是直角、对角线相等;菱形的四条边相等、对角线互相垂直.一组对边平行且相等或两组对边分别相等或对角线互相平分的四边形是平行四边形;有三个角是直角的四边形或对角线相等的平行四边形是矩形;四边相等的四边形或对角线互相垂直的平行四边形是菱形.同时,注意任何一个图形的定义既是判定定理,也是性质.故答案为:(1)C;(2)D;(3)D;(4)D.
例4(2015·南京)如图7,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
(1)求证:四边形EGFH是矩形;
(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.
由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形,要证平行四边形MNQP是菱形,只要证MN=NQ.由已知条件_____________________,MN∥EF,故只要证GM=FQ,即证△MGE≌△QFH.易证_____________________,________________________,故只要证∠MGE=∠QFH.易证∠MGE=∠GEF,∠QFH=∠EFH,__________________,即可得证.
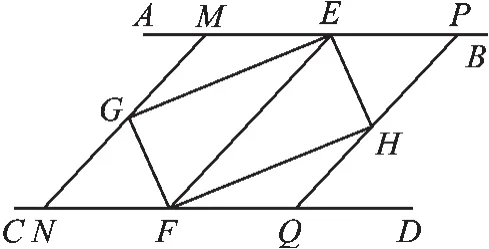
图7
【解析】(1)利用角平分线的定义结合平行线的性质得出∠FEH+∠EFH=90°,进而得出∠GEH=90°,进而有四边形EGFH是矩形;
(2)利用菱形的判定方法,要证▱MNQP是菱形,只需证MN=NQ,易证∠MGE= ∠QFH,即可得出.
例5(2015·荆州)如图8,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图9,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
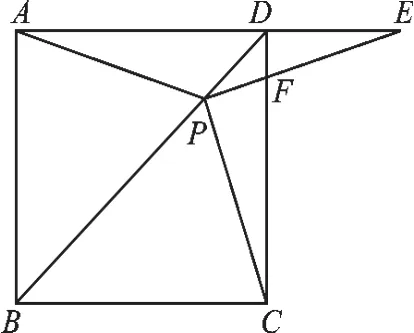
图8

图9
【解析】正方形具有矩形和菱形的一切性质.
(1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP = ∠BCP,进而得∠DAP=∠DCP,由PA=PE,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF= ∠EDF=90°得到结论;
(3)借助(1)和(2)的证明方法容易证明结论.
四、三角形的中位线
例6如图10,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=8,AO=6,则四边形DEFG的周长为().

图10
A. 12 B. 14 C. 16 D. 18

(作者单位:江苏省盐城市毓龙路实验学校)
