解开分式方程无解的困惑

王强济



解开分式方程无解的困惑

王强济

在初中数学教材中先后出现了可化为一元一次方程的分式方程和可化为一元二次方程的分式方程，让同学们感到特别困惑的就是有关增根和无解的问题，同学们常常会对这两个概念混淆不清，认为分式方程无解和分式方程有增根是同一回事，事实上并非如此.现就分式方程无解可能产生的情形举例说明如下：

一、不是只有产生增根时分式方程才会无解

1.原方程化去分母后的整式方程（一元一次方程）有解，但这个解却使原方程的分母为0，它是原方程的增根，从而原方程无解.

解：方程两边都乘（x+2）（x-2），

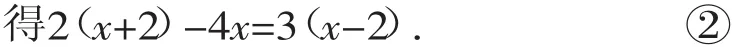
解这个方程，得x=2.

经检验：当x=2时，原方程无意义，

所以x=2是原方程的增根.

所以原方程无解.

【解析】显然，方程①中未知数x的取值范围是x≠2且x≠-2.而在去分母化为方程②后，此时未知数x的取值范围扩大为全体实数，所以当求得的x值恰好使最简公分母为零时，x的值就是增根.本题中方程②的解是x=2，恰好使公分母为零，所以x=2是原方程的增根，原方程无解.

2.原方程化去分母后的整式方程（一元一次方程）无解，从而原方程无解.

解：去分母后化为

x-1=3-x+2（2+x）.

整理得-1=7.

因为此方程无解，

所以原分式方程无解.

【解析】此方程化为整式方程后，本身就无解，当然原分式方程肯定就无解了.由此可见，分式方程无解不一定就是产生增根.

3.原方程化去分母后的整式方程（一元二次方程）有两个解，如果两个解都使原方程的分母为0，就都是原方程的增根，从而原方程无解.两个解中只有一个解使原方程的分母为0，它是原方程的增根，另一个解没有使原方程的分母为0，它就是原方程的根，从而原方程有解.可见分式方程产生增根不一定就会无解.

二、含参数分式方程无解时求参数需要分类讨论

解：原方程可化为

方程两边都乘x-2，

得x-3=-k.

解这个方程，得x=3-k.

因为原方程无解，所以这个解应是原方程的增根.即x=2，

所以2=3-k，

解得k=1.

故当k=1时，原方程无解.

【解析】因为同学们目前所学的是能化为一元一次方程的分式方程，而一元一次方程不是无解的情况时只有一个根，所以如果这个根是原方程的增根，那么原方程无解.不需要分类讨论.

解：方程两边都乘（x+2）（x-2），得

2（x+2）+mx=3（x-2），

整理得（m-1）x=-10.②

若原方程无解，则有两种情形：

（1）当m-1=0（即m=1）时，

方程②为0·x=-10，

此方程无解，所以原方程无解.

（2）如果方程②的解恰好是原分式方程的增根，那么原分式方程无解.原方程若有增根，增根为x=2或-2，

把x=2或-2代入方程②中，可求出m=-4或6.

综上所述，m=1或m=-4或m=6时，原分式方程无解.

【解析】做此类题首先将分式方程转化为整式方程，此整式方程本身就无解或有解是原方程的增根，需要分两类情形讨论，分别求出原方程中所含字母的值.若将此题“无解”改为“会产生增根”，则不需要考虑化为整式方程本身就无解的情形.

解：方程两边都乘（x+2）（x-2），得

2（x+2）+mx=3（x-2），

整理得（m-1）x=-10.②

如果方程②的解恰好是原分式方程的增根，那么原分式方程无解.原方程若有增根，增根为x=2或-2，把x=2或-2代入方程②中，求出m=-4或6.

所以当m=-4或6时，

原分式方程会产生增根.

弄清分式方程的增根与无解的区别和联系，分清分式方程无解各种情形有助于我们提高解分式方程时分析问题解决问题的能力.

（作者单位：江苏省连云港市新海实验中学）