从一道课本习题的解答谈分式求值题解决策略

王竞进



从一道课本习题的解答谈分式求值题解决策略

王竞进

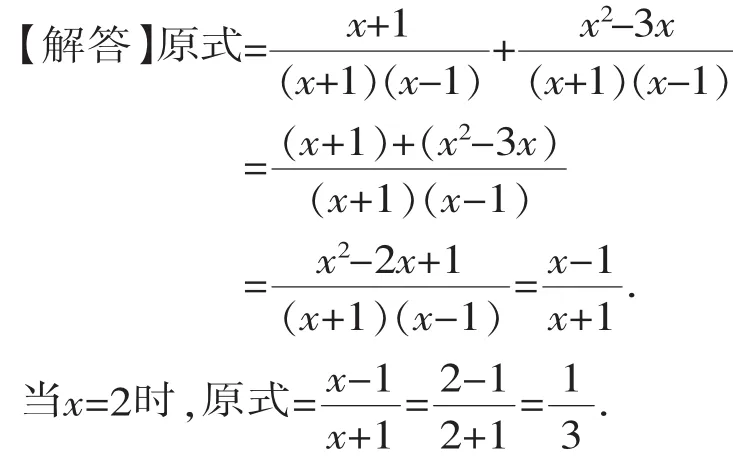
【反思】本题是义务教育教科书苏科版《数学》八年级下册第112页第4（1）题，它是一道典型的分式化简求值题.这类问题是常见的代数式求值题，往往先对分式化简，再将字母代入其中或选择一个能够使代数式有意义的字母值代入其中进行运算求得结果，有时也与不等式、方程联立设计成隐含条件求得分式的值.分式求值题往往得到中考命题者的青睐，现以近年来的中考题为例加以说明.

一、先化简，再求值

【解析】先应用分式的运算法则、基本性质对分式进行化简，再将字母代入其中计算求值.

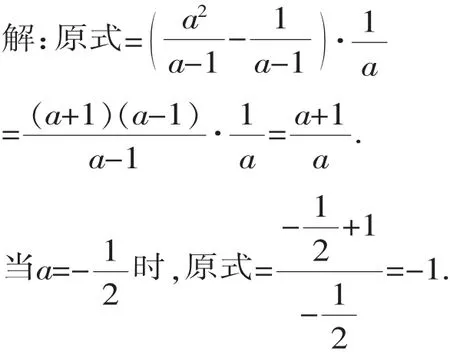
【策略】分式的求值题，往往先化简再代入求值比较简捷，直接代入其中较为繁琐且易错.

二、一次方程与分式求值题

【解析】根据分式运算的法则先把分式化简成最简分式，然后再求得未知数的值代入计算.

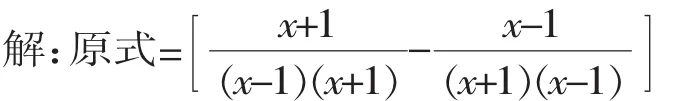
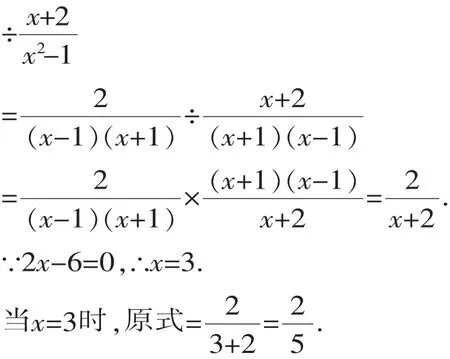
【策略】解答这类以一元一次方程的解为条件的分式的混合运算求值题，其关键是牢固掌握分式运算的法则与步骤，先化简分式，再求得一元一次方程的解，最后代入其中求结果.

【解析】本题考查了分式的化简求值，解题的关键是熟练掌握分式混合运算和利用非负数的性质列方程组求未知数的值.

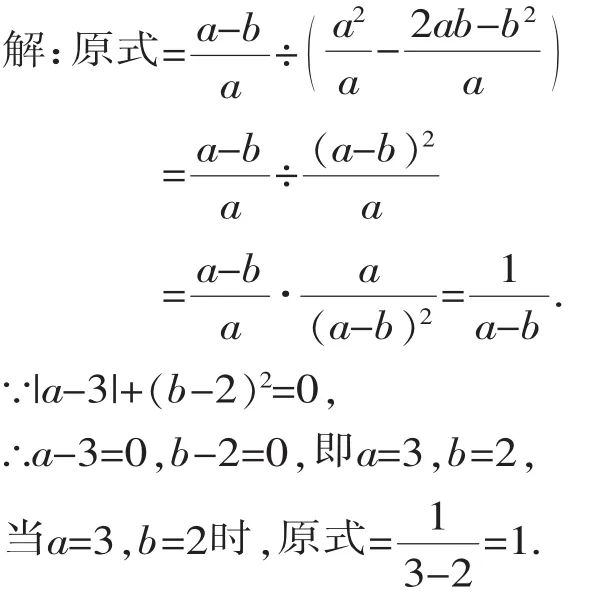
【策略】解答这类问题时，往往先应用非负数的性质建立方程组，求得方程组的解，最后代入化简后的分式中计算求得结果.

三、应用参数求分式的值

【策略】涉及两个字母的比值条件时，往往应用参数代入其中计算比较简便.

四、整体代入求分式的值

【策略】这类问题，往往先化简，再用含有一个字母的代数式作为整体代入其中进行计算求得结果.

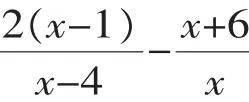
【解析】若是把方程x2-4x+1=0的根代入化简后的代数式中，计算过程会比较复杂，而且目前也不能求得方程的解.因此，先将分式通分，化为同分母分式后进行计算，再将已知条件适当变形为x2-4x=-1，而后把x2-4x看成整体代入求值.

【策略】本题没有直接求出字母x的值，而是把x2-4x看成是一个整体，巧妙地求得结果.本题渗透了整体代入的数学思想.

四、开放性条件求分式的值

【解析】先化简分式，再选择使分式有意义的x的值代入其中进行计算.

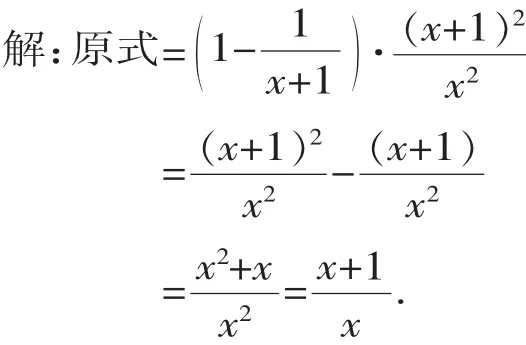
因为x+1≠0且x≠0，

所以x≠-1且x≠0，

【策略】这是一道自主性较强的分式化简求值题，能够较好地体现个性的差异性，选择的字母值一定要能够使原代数式有意义.特别要注意的是作为除式的分子不能为0哦！

【解析】先化简分式，再从所给的字母值中选择使分式有意义的字母x的值代入其中进行计算.

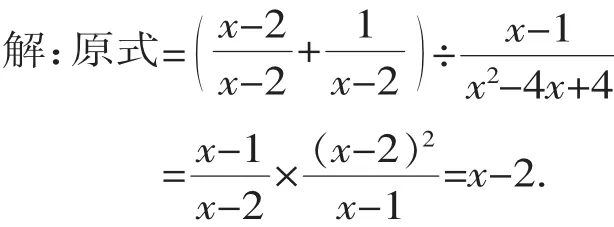
因为x-1≠0且x-2≠0，

所以x≠1且x≠2，

当x=3时，原式=3-2=1.

【策略】这类分式的化简求值题，选取喜欢的值代入时，注意要使所有分式及整个计算过程都有意义，不要落入“陷阱”中.

五、说理论证与求分式的值

（1）当x=3时，求代数式的值；

（2）原代数式的值能等于-1吗？为什么？

【考点解剖】本题考查了分式的化简求值.解题的关键是利用分解因式的方法化简分式.此时要注意把各分子、分母先因式分解，约分后再做减法运算；还要注意先把除法运算转化为乘法运算，然后约分化为最简形式.

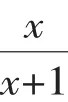
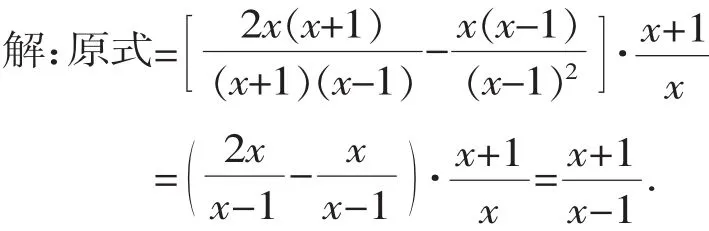
（1）当x=3时，原式=2；

∴x=0.

∴原代数式的值不能等于-1.

【策略】本题设计新颖，将求分式的值与分式方程融为一体，解答时既要正确进行分式的化简运算，也要正确进行分式值的解答，同时应明了求得的字母值还要能够使原分式有意义.

（作者单位：江苏省建湖县汇文实验初中教育集团汇文校区）