中考题中的几何变换

万中杰



中考题中的几何变换

万中杰

几何变换作为重要的研究手段和方法，在探索与发现图形的性质与图形的关系等方面有着极为广泛的应用.几何变换包括图形的平移、翻折与旋转.近几年中考中，出现了大量与此相关的问题.“平移、翻折与旋转”刻画的是两个全等图形特定的位置关系，任何图形通过“平移、翻折与旋转”后得到的新图形与原图形之间仅仅是位置发生了变化，而图形的形状与大小都没有变化.下面举例说明.

一、在平移中构造与发现

例1（2015·枣庄）如图1，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A′C′D′.

（1）证明△A′AD′≌△CC′B；

（2）若∠ACB=30°，试问当点C′在线段AC上的什么位置时，四边形ABC′D′是菱形，并请说明理由.

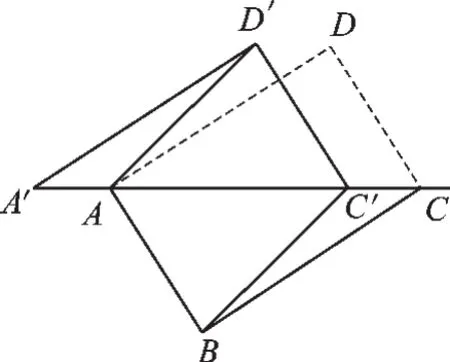
图1

【解析】（1）矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A′C′D′得A′D′=BC=AD，A′D′∥AD∥BC，AA′=CC′，∴∠D′A′C′=∠BCA，∴△A′AD′≌△CC′B.

（2）当点C′是线段AC的中点时，四边形ABC′D′是菱形，理由如下：

【点评】决定平移前后图形位置的两个基本因素是平移的方向和距离，本题通过“平移不改变图形的形状和大小”的性质，再结合平移前后图形的相应位置进行分析、综合、探究与解答.

二、在翻折中体验与发现

例2（2015·扬州）如图2，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l交CD边于点E，连接BE.

（1）求证：四边形BCED′是平行四边形；

（2）若BE平分∠ABC，求证：AB2=AE2+ BE2.

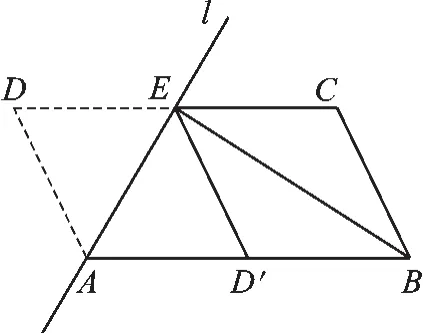
图2

【思路点拨】（1）利用翻折变换的性质以及平行线的性质，我们有∠DAE=∠EAD′=∠DEA=∠D′EA，进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形，进而求出四边形BCED′是平行四边形；

（2）利用平行线的性质结合勾股定理得出答案.

证明：（1）∵将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，

∴∠DAE=∠D′AE，∠DEA=∠D′EA，∠D=∠AD′E，

∵DE∥AD′，∴∠DEA=∠EAD′，

∴∠DAE=∠EAD′=∠DEA=∠D′EA，

∴∠DAD′=∠DED′，

∴四边形DAD′E是平行四边形，

∴DE=AD′，

∵四边形ABCD是平行四边形，

∴AB=CD，AB∥CD，

∴CE=D′B，CE∥D′B，

∴四边形BCED′是平行四边形；

（2）∵BE平分∠ABC，

∴∠CBE=∠EBA，

∵AD∥BC，∴∠DAB+∠CBA=180°，

∵∠DAE=∠BAE，

∴∠EAB+∠EBA=90°，

∴∠AEB=90°，

∴AB2=AE2+BE2.

【点评】图形的折叠问题是近几年中考试题常见题型.在解答此类问题时，要明白折痕两边的图形是轴对称图形，然后再利用轴对称变换的性质解题.它要求我们能根据题目中的折叠发现其中的变量与不变量，或者变化的趋势与内在联系，挖掘其中隐含的规律或相关的结论.

三、在旋转中构造与探究

例3（2015·甘南州）如图3，在△ABC和△EDC中，AC=CE=CB=CD；∠ACB= ∠DCE=90°，AB与CE交于F，ED与AB、BC分别交于M、H.

（1）求证：CF=CH；

（2）如图4，△ABC不动，将△EDC绕点C旋转到∠BCE=45°时，试判断四边形ACDM是什么四边形？并证明你的结论.

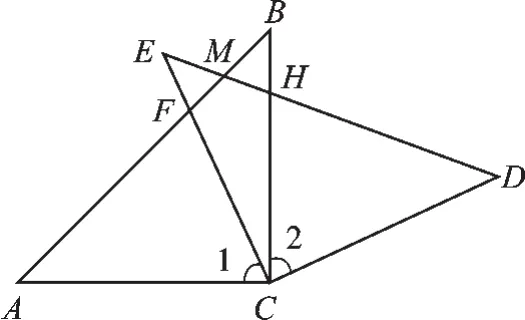
图3

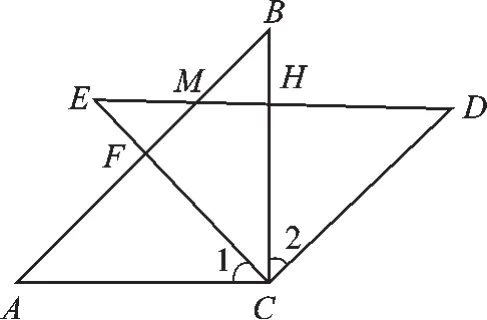
图4

【思路点拨】（1）要证明CF=CH，可先证明△BCF≌△ECH，由∠ACB=∠DCE=90°，AC=CE=CB=CD，可得∠B=∠E=45°，从而得出结论；

（2）根据△EDC绕点C旋转到∠BCE= 45°，推出四边形ACDM是平行四边形，又由AC=CD，从而判断出四边形ACDM是菱形.

【解析】（1）证明：∵AC=CE=CB=CD，∠ACB=∠ECD=90°，

∴∠A=∠B=∠D=∠E=45°.

在△BCF和△ECH中，

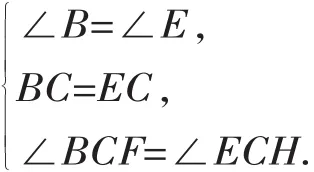
∴△BCF≌△ECH（ASA），

∴CF=CH（全等三角形的对应边相等）；

（2）解：四边形ACDM是菱形.

证明：∵∠ACB=∠DCE=90°，

∠BCE=45°，

∴∠1=∠2=45°.

∵∠E=45°，∴∠1=∠E，

∴AC∥DE，

∴∠AMH=180°-∠A=135°=∠ACD，

又∵∠A=∠D=45°，

∴四边形ACDM是平行四边形（两组对角相等的四边形是平行四边形），

∵AC=CD，∴四边形ACDM是菱形.

【点评】在旋转变换中要把握好三要素：旋转中心、旋转角和旋转方向，对于图形的旋转变换，在变化过程中的不变量、变化量以及由此构造出的新图形的形状、位置、大小关系要引起高度重视.解决这类问题的关键是以联系、发展的动态观点，捕捉和确定某些特殊的图形或位置，这样就可以找到解题思路.

例4已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG.

（1）求证：EG=CG；

（2）将图5（1）中△BEF绕B点逆时针旋转45°，如图5（2）所示，取DF的中点G，连接EG、CG.问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由.

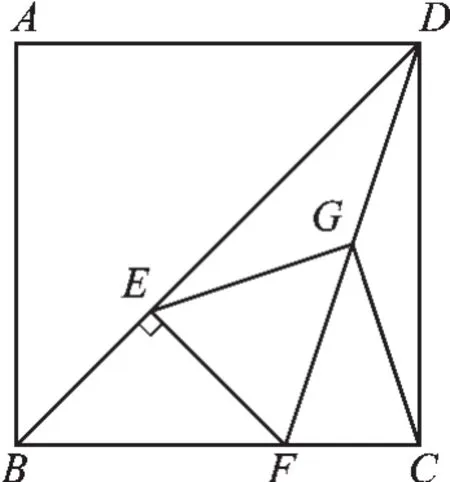
图5（1）

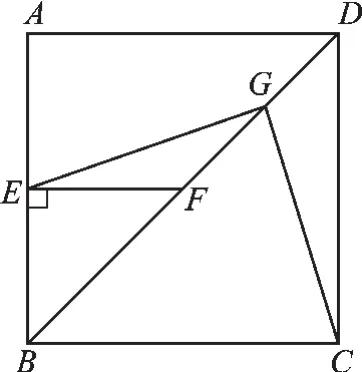
图5（2）

（3）将图5（1）中△BEF绕B点旋转任意角度，如图5 （3）所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）

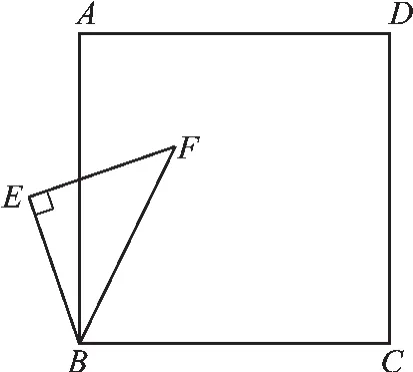
图5（3）

【思路点拨】（1）利用直角三角形斜边上的中线等于斜边的一半，可以证出EG= CG；

（2）△BEF绕B点逆时针旋转45°后，充分利用G为DF中点，通过添加辅助线，分别构造△DMG≌△FNG，△DAG≌△DCG，△AMG≌△ENG，从而得证；

【解析】（1）证明：在Rt△FCD中，

∵G为DF的中点，

∴CG=EG.

（2）（1）中结论仍然成立，即EG=CG.

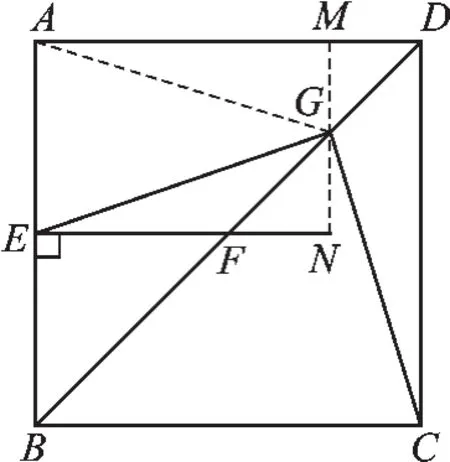
图6

连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点.

在△DAG与△DCG中，

∵AD=CD，∠ADG=∠CDG，DG=DG，

∴△DAG≌△DCG.∴AG=CG.

在△DMG与△FNG中，

∵∠DGM=∠FGN，FG=DG，∠MDG= ∠NFG，

∴△DMG≌△FNG.∴MG=NG.

在矩形AENM中，AM=EN.

在Rt△AMG与Rt△ENG中，

∵AM=EN，MG=NG，

∴△AMG≌△ENG，

∴AG=EG.∴EG=CG.

（3）（1）中的结论仍然成立，即EG= CG.其他的结论还有：EG⊥CG.

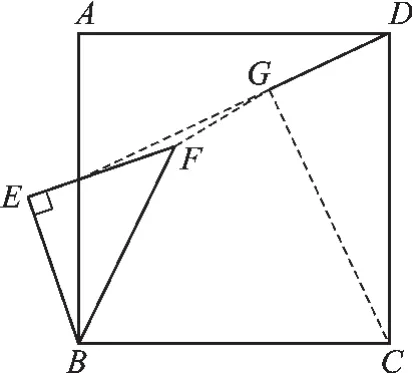
图7

【点评】充分挖掘相关图形的信息，关注图形的性质、定理，把题目中的某些隐含条件挖掘出来，并适当添加辅助线，化一般为特殊，化未知为已知，用从特殊到一般的思想，归纳猜想出结论.

对于“平移、翻折与旋转”这一类的问题，我们要紧紧抓住：变换后的图形，其形状不改变，大小不改变，只是位置发生改变.因此要通过寻找全等的图形，找到其中线（角）之间的联系，从而得出结论.