一道课本例题的再思考
——灵活运用特殊平行四边形的性质与判定
2016-06-01王金坤
王金坤
一道课本例题的再思考
——灵活运用特殊平行四边形的性质与判定
王金坤
苏科版八(下)80页例4:
已知:如图1,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.
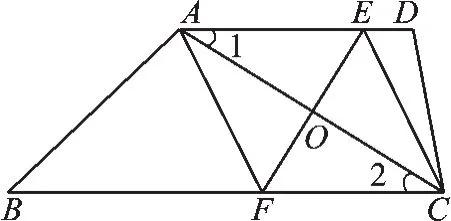
【评析】本例题在教材中安排在菱形的判定后.要证明菱形,可以先证明平行四边形,再证对角线互相垂直即可.课本上的解法是:
∵AD∥BC,∴∠1=∠2.
∵EF垂直平分AC,
∴OA=OC,∠AOE=∠COF.
∴△AOE≌△COF.∴OE=OF.
∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形).
又∵EF⊥AC,
∴▱AFCE是菱形(对角线互相垂直的平行四边形是菱形).
【反思】还能不能用其它方法证明菱形呢?答案是肯定的,在证得四边形AFCE是平行四边形后,可以得到AE=CF,而题目中已知EF垂直平分AC,所以AE=CE,AF= CF,这样就可以得到AE=CE=CF=AF.根据四边相等的四边形是菱形得到结论.当然我们也可以利用菱形的定义即一组邻边相等的平行四边形是菱形来证明.
【深入探究】
变式1如图2,矩形ABCD(AD>AB),对角线AC的垂直平分线与边AD、BC分别相交于点E、F,分别连接AF和CE.
(1)证明:四边形AFCE是菱形;
(2)若AB=4 cm,BC=8 cm,求BF的长.
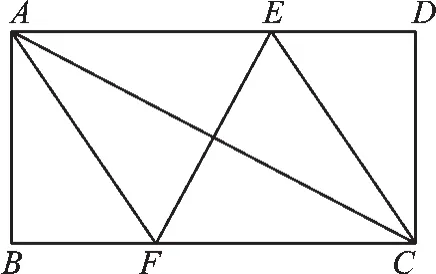
图2
【评析】菱形的性质和判定是在学习了矩形的相关知识之后,所以当题目中的条件由直接的AD∥BC换成矩形ABCD后,增加了难度.我们先要利用矩形的性质得到平行,再利用全等证平行四边形,进而证得菱形.
【解答】证明:如图3,设AC、EF相交于点O,

图3
(1)矩形ABCD中,AD∥BC,∴∠1=∠2.
∵EF垂直平分AC,
∴OA=OC,∠AOE=∠COF.
∴△AOE≌△COF.∴OE=OF.
∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形).
又∵EF⊥AC,
∴▱AFCE是菱形(对角线互相垂直的平行四边形是菱形).
(2)∵四边形AFCE是菱形,
∴AF=CF.设BF=x,
则CF=8-x,
在Rt△ABF中,AB2+BF2=AF2,
∴42+x2=(8-x)2,
∴x=3.即BF=3 cm.
变式2数学实验:你能用一张长方形纸片折叠出一个菱形吗?试试看?
【评析】我们可以按照变式1的方法,先折出一条对角线,再折出这条对角线的垂直平分线,最后沿着一些折痕,可以得到一个菱形.
【解答】如图4,先折出一条对角线AC,再折出AC的垂直平分线E,F,接着沿CE,AF折叠并剪开,得到一个四边形AECF,则这个四边形是菱形.(证明的方法同变式1)
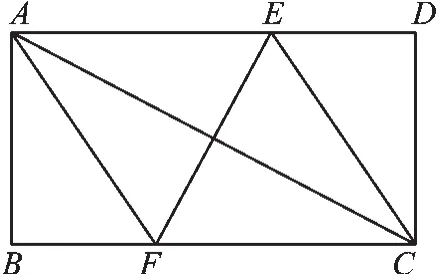
图4
变式3在▱ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE.
(1)如图5,试判断四边形EGFH的形状,并说明理由;
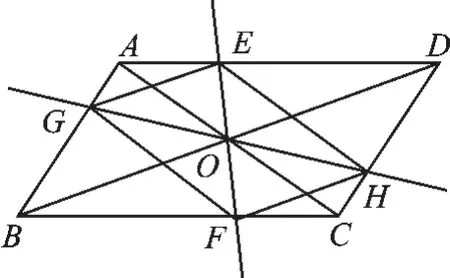
图5
(2)如图6,当EF⊥GH时,四边形EGFH的形状是_______;
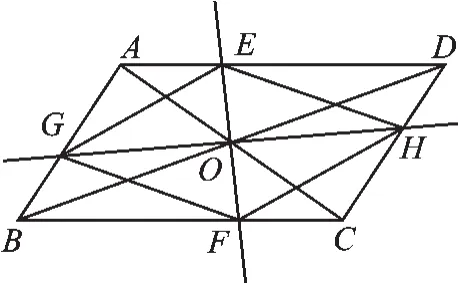
图6
(3)如图7,在(2)的条件下,若AC=BD,四边形EGFH的形状是_______;
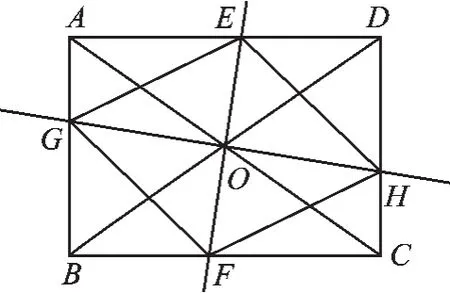
图7
(4)如图8,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.

图8
【评析】(1)由于平行四边形对角线的交点是它的对称中心,即可得到OE=OF,OG= OH,然后再根据对角线互相平分的四边形是平行四边形可判断EGFH的形状.
(2)当EF⊥GH时,平行四边形EGFH的对角线互相垂直平分,故四边形EGFH是菱形.
(3)当AC=BD时,对四边形EGFH的形状不会产生影响,故结论同(2);
(4)当AC=BD且AC⊥BD时,四边形ABCD是正方形,则对角线相等且互相垂直平分;
可通过证△BOG≌△COF,得OG=OF,从而证得菱形的对角线相等,根据对角线相等的菱形是正方形即可判断出四边形EGFH的形状.
【解答】(1)平行四边形;(2)菱形;(3)菱形;(4)正方形.
解:(1)四边形EGFH是平行四边形.
证明:∵▱ABCD的对角线AC、BD交于点O.
∴点O是▱ABCD的对称中心.
∴EO=FO,GO=HO.
∴四边形EGFH是平行四边形.
(2)菱形.
(3)菱形.
(4)四边形EGFH是正方形.∵AC=BD,
∴▱ABCD是菱形.又∵AC⊥BD,
∴▱ABCD是正方形,
∴∠BOC=90°,∠GBO=∠FCO =45°. OB=OC.
∵EF⊥GH,∴∠GOF=90°.
∴∠BOG=∠COF.∴△BOG≌△COF.
∴OG=OF,∴GH=EF.
由(1)知四边形EGFH是平行四边形,
又∵EF⊥GH,EF=GH.∴四边形EGFH是正方形.
(作者单位:江苏省盐城市毓龙路实验学校)
