“杀伤力”强的易错题剖析

顾友梅



“杀伤力”强的易错题剖析

顾友梅

分式运算是代数式运算的一种基本形式，是近年来中考的热点题型之一，鉴于其涉及的知识点较多，对同学们的综合能力要求较高，所以常常有相当一部分人在此受挫.下面笔者就以在教学过程中对大家造成很强“杀伤力”的试题为例，剖析原因，探求方法，以提高同学们解决这方面问题的能力.

一、对互为相反数的代数式理解不透

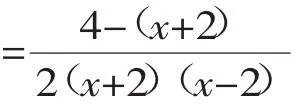
本题错在没有看出-x+2=-（x-2），因而没有将原分式继续约分，化成最简.所以正确解答应为：

这两题均是同学们在学习过程中产生错误较多的题，究其原因主要还是同学们对互为相反数的代数式认识不充分，造成不约分或乱约分.因此在学习时一定要重视此知识点的理解与应用.

二、对因式分解的知识掌握不牢

因式分解是中学数学中最重要的恒等变形之一，它被广泛地应用于初等数学之中，是我们解决分式运算等问题的有力工具，也是学好分式有关内容的基础.而很多同学到现在还对因式分解的方法、技巧等掌握不牢，导致分式运算的错误.

有的同学不知道1+4a+4a2可以分解为（2a+1）2，不能将分式进一步化简，从而造成求值繁琐出错.也有的同学没有把分式约分到最简形式.正确的解答为：

本题的错误是因为学生不会把a2-b2分解为（a+b）（a-b）导致没有将分式进一步化简.正确的解答应为：

三、对数学思想方法的应用不灵活

数学思想是指人们对数学理论的内容的本质认识，数学方法是数学思想的具体化形式.数学思想方法是数学学习的核心，初中数学中的许多问题蕴含着丰富的数学思想方法.分式运算中的化简及求值题是考查同学们的基础知识及创新能力的重要题型，由于对数学思想方法的应用不够灵活，某些试题对学生的“杀伤力”很大.

（1）整体代入思想

（2）转化思想

（3）消元代入思想（设参数）

（作者单位：江苏省连云港市新海实验中学）