例析与增根有关的分式方程解的问题

汤建明



例析与增根有关的分式方程解的问题

汤建明

解分式方程时，有时会产生增根.因此，解分式方程时，验根成了必不可少的步骤.分式方程有增根不一定无解，但如果解出的所有根都是增根，这时原分式方程就一定无解了.反之，分式方程无解可能原方程无解，也可能转化后的整式方程无解.巧妙利用其增根与方程之间的关系，可以帮助我们寻求解答与增根有关问题的解题策略，现举例说明，供大家参考.

一、根据方程增根求待定系数

A. m=-1B. m=0

C. m=3D. m=0或m=3

【剖析】方程两边都乘最简公分母（x-3），把分式方程化为整式方程，得2-x-m=2（x-3）.再根据分式方程的增根就是使最简公分母等于0的未知数的值求出x的值为3，所以2-3-m=2（3-3），解得m=-1.

【解答】本题应该选A.

【点评】解答这类方程增根问题，往往先根据最简公分母为0确定增根，再化分式方程为整式方程，最后把增根代入整式方程即可求得相关字母的值.

二、根据方程无解确定待定系数值

【剖析】分式方程两边乘最简公分母（x+2）（x-2），得关于x的一元一次方程m-（x-2）=0，解得：x=2+m.由于该分式方程的增根可能是x=2，也可能是x=-2.当x=2时，2+ m=2，∴m=0时方程无解；当x=-2时，2+m=-2，∴m=-4时方程无解.因此，m=0或m=-4.

【解答】本题应该填：m=0或m=-4.

【点评】分式方程无解的条件有两种：（1）分式方程化成的整式方程无解，则分式方程也无解；（2）化成的整式方程的解都是该分式方程的增根，均被舍掉，则分式方程无解.本题属于第2种情形，需要对方程的两个增根进行分类讨论.

【解答】本题应该填：1或-1.

【点评】本题从两种情形分别加以讨论：分式方程化成的整式方程无解，则分式方程也无解；化成的整式方程的解也是该分式方程的增根，则分式方程无解.

三、根据方程有解确定待定系数的取值范围

A. a=5或a=0 B. a≠0

C. a≠5D. a≠5且a≠0

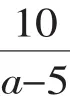
【解答】本题应该选D.

【点评】解答这类问题时，往往先根据所给的分式方程有解的条件确定转化为整式方程有解，进而取值确定其中待定系数的取值范围，再应用分式方程有解隐含其解不可能是增根的条件，求得待定系数取值范围.

A. 2B. 1

C.不为±2的数D.无法确定

【剖析】去分母，把分式方程化为整式方程，x（x+1）-k=x（x-1），解关于k的方程，得k=2x.由题意，分式方程无增根，则公分母（x+1）（x-1）≠0，即x≠-1且x≠1，则k≠±2.

【解答】本题应该选C.

【点评】方程无增根，就意味着对应的整式方程的根使分式方程的公分母不等于0，利用这一点可以确定字母系数的值或取值范围.

四、根据方程解的取值确定待定系数取值范围

A. m＞-1B. m≥-1

C. m＞-1且m≠1D. m≥-1且m≠1

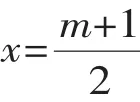
【解答】本题应该选D.

【点评】解答这类问题时，往往先根据所给方程解的取值确定转化后整式方程解的取值范围，从而确定其中待定系数的取值范围，再挖掘方程中隐含的增根条件求得待定系数取值范围.

（作者单位：江苏省建湖县城南实验初中教育集团城南校区）