《分式》学习要点

王竞进



《分式》学习要点

王竞进

《分式》是初中数学重要内容之一，它涵盖：分式的概念，分式的基本性质，分式的约分与通分，分式的加、减、乘、除及乘方运算，分式方程的概念以及可化为一元一次方程的分式方程的解法.学习本章时，需要抓住以下几个要点.

一、认清基本概念

2.根据分式的基本性质，把一个分式的分子和分母分别除以它们的公因式，叫做分式的约分.分子与分母没有公因式的分式叫做最简分式.

3.根据分式的基本性质，把几个异分母的分式变形成同分母的分式，叫做分式的通分，变形后的分母叫做这几个分式的公分母.几个分式中各分母系数（都是整数）的最小公倍数与所有字母的最高次幂的积叫做这几个分式的最简公分母.

例1下列式子中是分式的是（）.

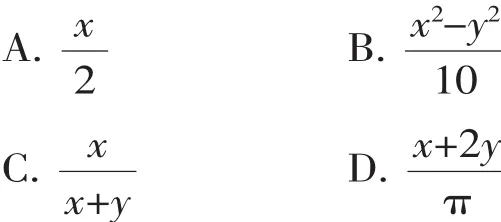
【解答】所给的四个选项中，选项A、B中的分母都是有理数、不含字母，选项D的分母是无理数π，而不是字母，只有选项C中含有字母，因此，本题答案为C.

【说明】要判别所给的代数式是否分式，只需要从形式上加以判别，只要分母中含有字母就是分式.如代数式就是分式，而代数式就不是分式.

二、理解基本性质

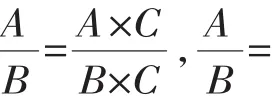
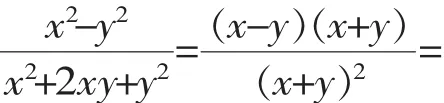
例2下列等式成立的是（）.

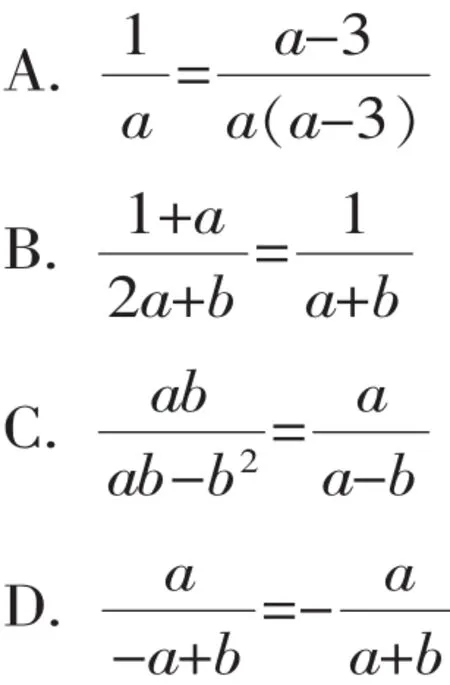
【解答】选项A，不能说明这个整式（a-3）一定不等于0，因此，不符合分式的基本性质，是错误的；选项B，将分式的分子与分母分别减去整式a，不符合分式的基本性质，是错误的；选项C，将分式的分子与分母分别除以整式b，根据分式的意义，这个整式b一定不等于0，因此，符合分式的基本性质，是正确的；根据分式的基本性质，改变分子、分母和分式中两项的符号，分式的大小不变，选项D，分式分母中仅仅改变第一项的符号，因此，是错误的.所以，本题答案为C.

【说明】分式的基本性质是分式变形与化简的依据.

三、掌握运算法则

1.同分母分式加减运算的法则

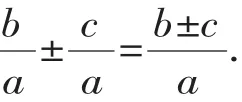
2.异分母分式加减运算的法则

3.分式的乘法法则

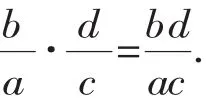
4.分式的除法法则

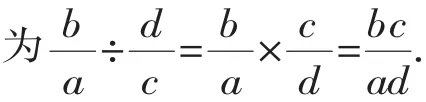
【解答】先将两个分式通分化为同分母分式，再加减，然后约分化简，即：

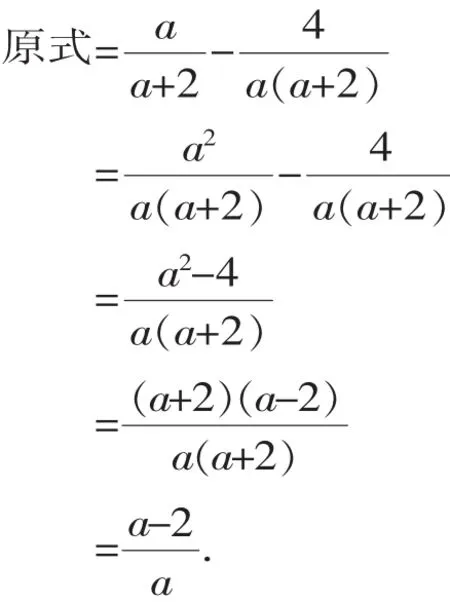
所以，本题应该填：

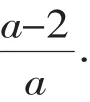
【说明】分式的加减运算，要先看分母是否相同，分母相同时，直接把分子相加，分母不同时，需要找到各分母的最简公分母进行通分把异分母分式化为同分母分式.分式运算的结果必须是最简分式或整式.

【解答】先利用分式的加减法则计算出括号里的部分，然后再根据分式的除法法则进行计算可得结果，即：

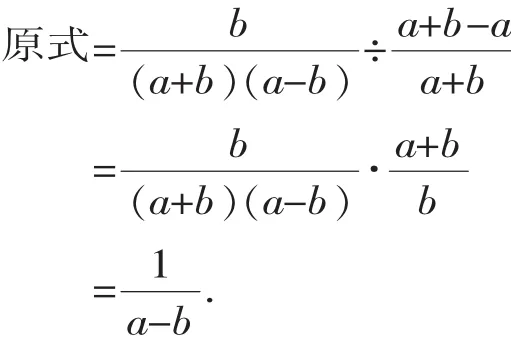
【说明】进行分式的加、减、乘、除混合运算时，先乘除，后加减，如果有括号，先进行括号内的运算.

四、会解分式方程

解分式方程的一般步骤：（1）去分母，把分式方程化为整式方程；（2）解这个整式方程；（3）检验；（4）写出结论.

A. x=2B. x=6

C. x=-6D.无解

【解答】将方程两边同时乘x（x-2）得：3（x-2）=2x，解得x=6.检验：当x=6时，x（x-2）=24≠0，因此，x=6是原分式方程的解，故选择B.

【说明】在分式方程的左右两边同时乘分式方程的最简公分母，将分式方程转化为整式方程.解分式方程与整式方程的不同之处在于：求出未知数的值后必须验根，因为在把分式方程化为整式方程的过程中，扩大了未知数的取值范围，可能产生增根.验根时把整式方程的根代入最简公分母，如果最简公分母等于0，这个根就是增根，否则这个根就是原分式方程的根.若解出的根都是增根，则原方程无解.

五、能构建分式方程模型解决实际问题

例6（2015·随州）端午节前夕，小东的父母准备购买若干个粽子和咸鸭蛋（每个粽子的价格相同，每个咸鸭蛋的价格相同）.已知粽子的价格比咸鸭蛋的价格贵1.8元，花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同，求粽子与咸鸭蛋的价格各多少？

【解答】本题中隐含的相等关系式为：花30元购买粽子的个数=花12元购买咸鸭蛋的个数.因此，可以建立方程解决问题.

设咸鸭蛋的价格为x元，则粽子的价格为（1.8+x）元，根据题意得：

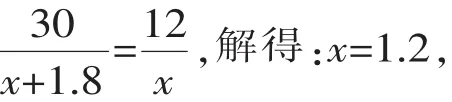
经检验x=1.2是所列分式方程的解，且符合题意，

则1.8+x=1.8+1.2=3（元）.

答：咸鸭蛋的价格为1.2元，粽子的价格为3元.

【说明】列分式方程解应用题和列整式方程（组）类似，要抓住已知条件中的等量关系式建立方程.特别要注意的是：必须从两个角度对求得的根进行检验，既要检验所求未知数的值是否适合原方程，还要检验此解是否符合实际意义.

（作者单位：江苏省建湖县汇文实验初中教育集团汇文校区）