热声制冷机板叠内气体的微观热力循环分析

汪建新 阚小美 孟 楠 李 东

(内蒙古科技大学机械工程学院 包头 014010)

热声制冷机板叠内气体的微观热力循环分析

汪建新 阚小美 孟 楠 李 东

(内蒙古科技大学机械工程学院 包头 014010)

基于线性小振幅声场，探讨了气体微团与固体板叠之间能量传递规律，系统地分析了谐振腔板叠内的热力过程。利用物理上直观的拉格朗日法，阐述了气体微团与固体板叠之间的热量交换。通过分析一个气团总声能量的变化图，直观地了解气体微团与固体板叠之间热量交换的数值变化关系。结果表明驻波型声场板叠中的不同气体微团之间，像是一个个配合精巧、功能齐全的微型制冷机，气体微团通过接力作用，实现板叠上热量的搬移，在低温端得到制冷量。

热声制冷 微观热力循环 声场分布 板叠 热量传递

1 引 言

所有热声产品的工作原理都基于所谓的热声效应。热声效应一般发生在距离壁面一个热渗透深度的范围内，因此为了加强热声效应的强度，必须增大气体与固体的接触表面。采用板叠结构可大大提高二者的接触面积，从而对提高热声制冷机的效率有非常重要的意义[1]。板叠内的气体微团在驱动声压波动作用下，在其平衡位置附近做微小振动。在一个声波周期内，气团往复运动一个循环，压力增大时被压缩，吸收声功，同时温度升高；压力降低时气体膨胀，对外做功，同时温度降低[2]。本文主要分析气体在声压波动作用下的功能转换和与板叠之间的热量交换。

要计算板叠两端形成的温度梯度，假设谐振腔内声波是一种平面波，在声场中延板叠轴向的任意位置，声压的振幅是不同的。也就是说在每一个不同位置的气团，都在振幅确定的声压波动作用下，在平衡位置左右两侧做微小振动[3]。板叠两侧的气体与板叠之间功能转换的数量值延板叠轴向方向是不同的，板叠与气体微团的换热也因此不同，当满足一定条件时，可以在板叠上形成一个温度梯度。

基于以上思路，热声制冷机热力部件的完整功能需要从微观尺度上加以分析考虑。本文将建立热声制冷机中关键热力部件板叠上的微观热力循环模型，并对其工作机理进行分析和讨论，给出板叠上形成温度梯度的条件及温度梯度的大小。

2 板叠间振荡气体的能量模型

谐振腔内的声场是相当复杂的，工作条件的不同会导致谐振腔内气体微团热力过程的极大差异。本文采用拉格朗日法分析气体微团的运动状态。首先假设：

(1)气体为无粘性的理想气体，即气体之间不会相互影响，流动是无粘性的；

(2)气体没有流动损失和热量损失；

(3)气体微团往复运动与固体板叠之间具有理想的换热，因此气体与固体之间能够随时保持热平衡。

(4)谐振腔内的声场为线性小振幅声场，声波为平面波。

在上述假设条件下，板叠不存在热力损失，循环过程可以认为熵产为零，即工作过程是可逆的[4]。

以板叠内的一个气体微团为例进行分析，气团位于板叠上方热渗透深度范围内。设在没有声扰动时气体介质的密度为ρ0，它不随时间和位置的变化而改变，所选择气体微团的体积为V0。在声压波动作用下，气体微团做微小的往复运动，动能增加，同时随着声压值增加，气团体积收缩，吸收声功，气体微团具有了位能，气体微团总的声能量为动能与位能之和[5]。

根据流体力学的3个基本方程，可以推导出一个气体微团的运动状态。由于谐振腔内的声场是小振幅声场，可以将基本方程进行线性化处理，得到简化的3个基本方程[6]：

运动方程：

(1)

连续性方程：

(2)

物态方程：

(3)

由于气体微团被压缩和膨胀过程中认为质量保持不变，气体微团所获得总的声能量为：

(4)

式(4)为一般声场中声能量变化的普遍表达式，其中u为气团沿板叠轴线方向运动速度。不难看出，该式是标量表达式，只能表示能量的大小变化情况。

3 不同型声场中的换热情况分析

3.1 不同型声场中相关参量随时间的变化规律

根据热声制冷机的特点，谐振腔内的声波为平面声波。可以用分离变量法求解一维声波方程，得到声场的解为[5]：

行波型声场：

(5)

驻波型声场：

(6)

可见声压函数为复数，有实部和虚部两部分，通常可用复平面上的一个点来表示。该点的横坐标即为函数的实数部分，纵坐标即为虚数部分。同时，它也可以用由原点到复平面上这一点的矢量来表示。式(5)和(6)可以用余弦函数与正弦函数的组合表示出来。一般取实数部分进行分析[7]，因为一个复函数为方程的解，那么，它的实部与虚部也各自都是此方程的解。也可以只取复数函数的虚数部分，因为虚部也是方程的解。

只考虑实数部分，再由运动方程(1)得出气团速度表达式[5]：

(7)

对于行波型声场，有：

(8)

对于驻波型声场，有：

(9)

进一步得气团运动的位移与时间的变化关系。

对于行波型声场：

(10)

对于驻波型声场：

(11)

总声能量表达式：

行波型声场：

(12)

驻波型声场：

(13)

图1为行波型声场中任意位置处的气团所受压力、速度、振动位移和总的声能量随时间的变化曲线。

图1 行波型声场中各参量随时间变化关系Fig.1 Changes of various parameters with time in travelling-wave sound field

显然，气团在平衡位置时，所受声压力与速度为最大值，气团运动到左右两侧极限位置时，压力与速度同时为零。此运动规律与所学的质点自由振动情况不同。这是由于声场中的能量不是贮存在系统中，而是具有传递特性的[8]。

这类系统被称为非保守系统，即气体除了受到压力，还受到粘性阻尼力的作用，使得原本能量守恒的保守系统变为能量耗散的非保守系统。气体微团所获得的能量，会使其自身温度发生变化，从而与固体板叠发生热量交换，将自身增加的温度传递给板叠，同样自身温度减少时将从板叠吸收热量。在粘性阻尼力与声压力共同作用下，气体微团的运动速度与压力同相变化，这一点不能用保守系统质点的运动规律来解释。

由于声能量是标量，根据温度定义，气团的温度与气团内能是密切相关的，图1中声能量变化曲线反映声能量全部转化成气体内能时，气体内能随时间的变化规律，它只反映温度的大小变化而不能表明温度的变化方向。

由于谐振腔内声场为小振幅声场，则在微小的时间段dt内，压力变化dP时，气团体积变化dV，由气体状态方程得气团温度变化为：

(14)

式中：n为气体的物质的量，mol；T为热力学温度；R=8.31J/K/mol为气体常数。

显然，当气团所受压力增加，气团温度升高；气团所受压力减小，气团温度降低，且二者变化的相位相同。

在波向前传播过程中，假设在下一个时刻，波从声源处向前传播，则气团所受压力、速度和能量的变化如图1中虚线所示。显然，随着声波的传播，每一个位置上的气团都会经历相同振幅的压力波动，即每个位置气团的温度变化规律均相同。对于声场中位置固定的板叠，在进行热量交换时，板叠上方温度最高的气团相对于板叠的位置始终在改变，无法在板叠两端形成温度梯度。

而对于驻波型声场，在不同位置处的气体微团所受压力、气团速度、振动位移和所获得总的声能量随时间的变化关系曲线如图2所示。

图2 驻波型声场中各参量随时间变化关系Fig.2 Changes of various parameters with time in standing-wave sound field

由图2可知，驻波型声场中的声压值与气团速度之间的相位差为90°，当波从x=x1处传播到x=x2处时，原气团所受压力、速度、位移与能量随时间变化曲线如图2虚线所示。随着波向前传播，波形保持不变，相位的变化只会影响随时间变化的压力波、速度波与能量波振幅的大小。存在节点是驻波型声场的重要的特征。

在声压波动作用下，气团获得的总声能量时刻发生改变。随着波向前传播，相位的变化只影响气团总声能量的变化振幅，即气团的温度变化值随着位置的不同而发生改变。因此，谐振腔内延轴线方向，总是存在位置固定的温度最大值点和温度最小值点。只要放置板叠的位置合适，板叠附近的气团能够保持平衡位置一侧的温度始终高于(或低于)另一侧的温度。气团的连续往复运动维持了稳定的热量搬移过程，从而在板叠上形成温度梯度。

通过上述结论，可知在驻波型声场的板叠中具备热量搬移的条件，理论上能够形成温度梯度。

3.2 气体微团与板叠之间的换热分析

由分析知，声场中的气团受到的声压数量级远大于气团速度的数量级，因此虽然声能量流入或流出气团，但气团的温度变化与压力同相，振动速度对温度的影响可忽略不计。当谐振腔中形成稳定的声场以后，任一时刻谐振腔内延板叠轴线(谐振腔轴线)的能量波形都是已知的。无论是行波型还是驻波型声场，气团获得的总声能量都会在一个固定平均值上下波动，而气团获得总声能量的变化值即为气体内能的变化值。而系统中的能量是具有传递和转化特性的，流入或流出气团的总声能量转化成气团自身内能的变化，从而使气团温度发生改变。在一个循环周期内，对于气团温度与板叠温度，二者总有趋于相同的趋势。因此，气团温度高于与之接触的固体板叠温度时，气团将会对固体板叠释放热量，同理气团温度低于板叠温度时，气团将会从板叠吸收热量。

3.2.1 行波型声场中热量的传递

为分析气团在一个运动周期内与板叠之间的换热关系，将气团的运动分为四个热力过程，把气团处于平衡位置左侧的极限位置作为循环的起始点，4个时间段为：0<ωt<π/2，π/2<ωt<π，π<ωt<3π/2，3π/2<ωt<2π，分别对应图1压力曲线中所标示的热力过程①至热力过程④。

其对应的气团运动示意图如图3所示。

图3 行波型声场中气体微团运动示意图Fig.3 Motion diagram of gas micelle in travelling-wave sound field

由图1中能量随时间变化的曲线可知，流入或流出气团的总声能量按余弦规律改变。在热力学中，温度被定义为：

(15)

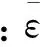
设气团未受到声扰动时的初始温度为T0，则在行波型声场中，气团位于左右两侧极限位置时所受声压力为零，温度为T0。下面分别分析4个不同的热力循环过程。

(1)热力过程①

如图2所示，气团从位置a运动到位置b，压力增加，气团内有声能量流入，气团温度从T0开始增加，温度随时间的变化关系为：

(16)

(17)

在这一过程中，气团温度逐渐增加，高于板叠温度，因此会将热量传递给板叠。由于越接近平衡位置b处，气团温度越高，与板叠之间的温度差越大，从而传递给板叠的热量越多。

(2)热力过程②

这一过程中气团继续向右运动，从位置b运动到位置c，压力与速度由最大值减小为零。声能量流出体积元，即气团内能减小，温度降低。到达位置c时，气团达到与a位置相同的状态，温度减小为T0。温度随时间的变化关系为：

(18)

在这一过程中，气团温度逐渐减小，但仍高于板叠温度，因此会继续将热量传递给板叠。由于越远离平衡位置b处，气团温度越低，与板叠之间的温度差越小，从而传递给板叠的热量越少。当到达位置c时，不再发生热量交换。

(3)热力过程③

此过程内，气团开始向左运动，从位置c返回到位置b，压力从零继续减小，声能量继续流出体积元，即气团内能减小，温度从T0继续降低。温度随时间变化关系为：

(19)

(20)

因此在第2次到达b位置时，气团温度达到最低。在这一过程中，气团温度继续减小，低于板叠温度，因此会从板叠吸收热量。越接近平衡位置b处，气团温度越低，与板叠之间的温度差越大，从而从板叠吸收的热量越多。这一过程气团所吸收的热量恰好与过程②气团释放的热量相等，相互抵消。

(4)热力过程④

同理分析这一过程气团的运动情况，气团温度逐渐增加，但仍低于板叠温度，因此会继续从板叠吸收热量。温度随时间变化关系为：

(21)

由于越远离平衡位置b处，气团温度越高，与板叠之间的温度差越小，从板叠吸收的热量越少。返回位置a时温度变为初始温度T0，不再发生热量交换。这一过程气团所吸收的热量恰好与过程①气团释放的热量相等，相互抵消。

根据上述分析可知，在行波型声场中，气体微团与固体板叠之间只进行热量的传递，一个气团在第一次经过平衡位置时产生的热量，恰好与第二次返回平衡位置时吸收的热量相互抵消，而在板叠上没有发生热量的搬移过程。随着波不断的向前传播，行波型声场中，任一位置的气团均会发生相同的热力循环过程。每一个气团在运动过程中都会与板叠之间进行热量的交换，但无法将热量从板叠的一侧搬移到另一侧，在板叠上无法形成温度梯度。

3.2.2 驻波型声场中热量的搬移

按照行波型声场的分析方法对驻波型声场中的气团进行分析，同样将气团的运动分为4个热力过程，分别对应图2中压力曲线所标示的位置，其对应的气团运动示意图如图4所示。

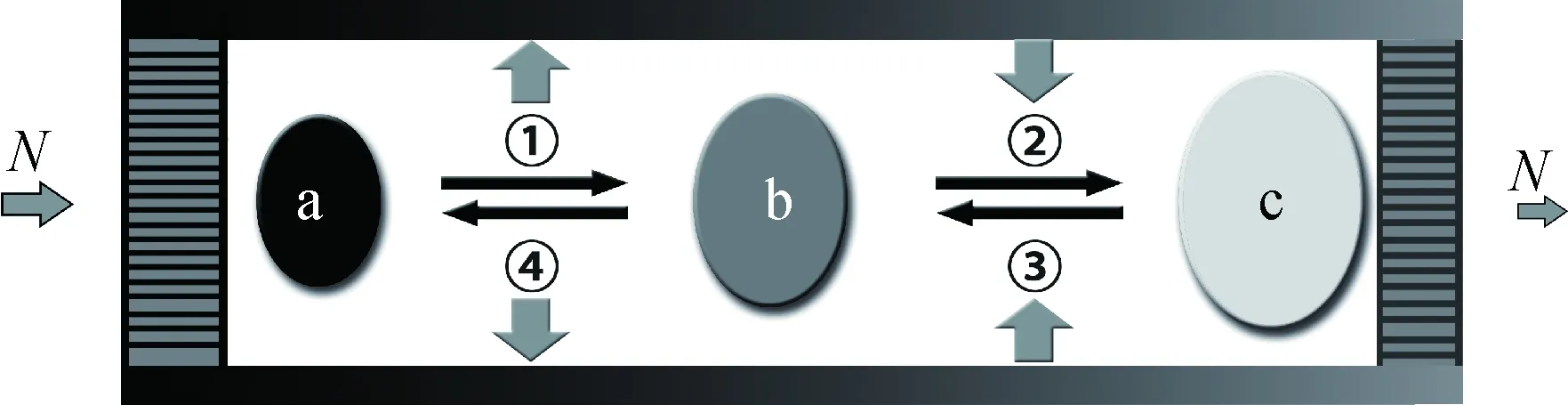
图4 驻波型声场中气体微团运动示意图Fig.4 Motion diagram of gas micelle in standing-wave sound field

(1)热力过程④和热力过程①

与行波型声场不同，驻波型声场中的气团在运动到平衡位置时所受压力为零，即平衡位置时气团未受声扰动，处于初始状态，气团温度为T0。假设气团从平衡位置b处开始做往复运动，首先分析热力过程④。气团从位置b运动到位置a，压力增加，气团内有声能量流入，气团温度从T0开始增加，温度随时间的变化关系为：

(22)

(23)

可见温度的变化与相位有直接关系。首先只讨论某处一个气团，在这一过程中，气团温度逐渐增加，高于板叠温度，因此会将热量传递给板叠。由于越远离平衡位置b处，气团温度越高，与板叠之间的温度差越大，从而传递给板叠的热量越多。气团继续运动，经历热力过程①，此过程中气团的运动恰好与过程④相反，气团所受压力减小，温度由最高值降低为初始状态，温度随时间的变化关系为：

(24)

此过程气团温度逐渐降低，但仍高于板叠温度，且气团运动到每个位置时的温度都与过程④中气团运动到相同位置时的温度相等。因此可将过程④和过程①看作一个绝热压缩过程和一个等温放热过程。即气团向左侧极限位置a处运动，经过绝热压缩过程，温度升高；返回平衡位置b的过程中，经历等温放热过程，将热量传递给板叠。

(2)热力过程②和热力过程③

气团继续向右运动，经历热力过程②，从位置b运动到位置c，压力继续减小为反向拉力，声能量流出体积元，气团温度从T0开始减小，温度随时间的变化关系为：

(25)

(26)

对于任意位置一个气团，在这一过程中，气团温度逐渐降低，低于板叠温度，因此会从板叠吸收热量。由于越远离平衡位置b处，气团温度越低，与板叠之间的温度差越大，从板叠吸收的热量越多。气团继续运动，经历热力过程③，气团所受压力开始增加，温度升高，到达平衡位置b时，气团回到初始状态，温度变为T0。温度随时间的变化关系为：

(27)

此过程气团温度逐渐升高，但仍低于板叠温度，气团运动到每个位置时的温度都与过程②中气团运动到相同位置时的温度相等。因此可将过程②和过程③看作一个绝热膨胀过程和一个等温吸热过程。即气团向右侧极限位置c处运动，经过绝热膨胀过程，温度降低；返回平衡位置b的过程中，经历等温吸热过程，从板叠吸收热量。综上所述，同一个气团在平衡位置右侧吸热，到左侧放热，实现热量的搬移。

4 结果分析

对一个气体微团来说，往复运动一个周期，就会在一个微段上形成微小的温度差，一个气团就是一个微型制冷机。由温度随时间的变化曲线可知，气团温度的变化与气团在声场中的位置有关。气团在左右两侧极限位置时温度分别达到最高与最低，温度差为：

(28)

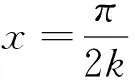
驻波型声场的谐振腔内，每个气团都在其平衡位置附近做往复运动，且每个气团都有微小的热量搬移作用。气团与邻近气团之间形成接力，在板叠上形成温度梯度。在无数个微型制冷气团循环运动进行接力以后，在板叠上应出现固定的高温区域与低温区域。当谐振腔内声场达到稳定状态，谐振腔内的气体会从外界吸收声能量，从而维持驻波振荡。将时间作为定值，以位置x作为变量，得到谐振腔内压力与气团总能量随位置的变化曲线，如图5所示。

图5 压力与气团总能量随位置变化曲线Fig.5 Curve of sound pressure and total energy with position change

5 结 论

本文从拉格朗日的观点分析了板叠内气体微团的热力过程和热力循环。通过分析一个气团的运动过程，得到如下结论：

(1)行波型声场和驻波型声场中，能量的变化方式是不同的。行波型声场中的能量时刻按最大的振幅波动，每个位置处的气团温度都是在理论上能够达到的最大值与最小值之间波动，放热量与吸热量都能达到最大状态，因此能够保证热量传递效率的最大化。但由于随着位置的改变，温度最高点始终在移动，因此不能在板叠上形成稳定的温度差。而驻波型声场中存在波节点，使得在某一特定区域，总能保证平衡位置一侧气团的温度始终高于另一侧气团的温度，从而在板叠上能够形成恒定的温度差。

(2)在进行热量交换时，行波型声场中的气团在第1次运动到平衡位置时，温度最高，将热量传递给板叠，而第2次返回到平衡位置时，温度达到最低，从板叠吸收热量，整个过程中，气团只是与板叠之间传递热量，并没有将板叠上的热量从一端搬移到另一端。驻波型声场中，由于气团在平衡位置两侧的极限位置时分别达到最高温度与最低温度，从而能够实现热量的搬移。

(3)在驻波型声场中，由于声压力波的不断扰动，内部气团的能量将发生振荡，能量振荡导致气团自身发生温度的振荡。振荡过程中，气团温度高于板叠温度时，会将热量传递给板叠；气团温度低于板叠温度时，将从板叠吸收热量。通过推导得到了达到平衡状态时板叠两端的温度梯度。

(4)本文只从微观层面上进行分析，即一个单位体积气团与板叠之间相互作用能够产生热量搬移，从而求得在板叠上形成的温度梯度。若要求宏观上总的换热量与板叠上总的温度梯度，就要从板叠的形状，尺寸等参数和气体的热渗透深度和粘性渗透深度等方面进行考虑，这些问题将在后续的工作中继续研究分析。

1 罗二仓,戴 巍,吴张华,等. 交变流动热机的介观热力循环理论 第一部分 制冷机回热器的介观热力循环模型及分析[J]. 低温工程,2004(1):1-11.

Er Cang Luo, Dai Wei, Wu Zhanghua, et al. Meso-scope thermodynamic theory for cyclic flow engines.first part:meso-scope thermodynamic model for cyclic flow regenerator[J].Cryogenics, 2004(1):1-11.

2 黄 竞,何雅玲,李 茹. 热声制冷机板叠内流动与换热的数值分析[J]. 工程热物理学报,2008(5):737-740.

Huang Jing, He Yaling, Li Ru. Numerical analysis of the flow and heat transfer in the stacks of the thermoacoustic refrigerator[J].Journal of Engineering Thermophysics,2008(5):737-740.

3 张富珍，李 青，孙生生,等.热声系统内交变流动特性的理论分析[J].低温工程，2008(1):11-15.

Zhang Funzhen, Li Qing, Sun Shengsheng,et al. In alternating thermoacoustic system theory analysis of flow characteristics[J]. Cryogenics, 2008(1):11-15.

4 A T A M de.Waele,P P Steijaert,J Gijzen.thermodynamic-al aspects of pulse tubes[J].Cryogenics,1997,37:313.

5 杜功焕,朱哲民,龚秀芬. 声学基础(第三版)[M]南京:南京大学出版社,2012:183-191.

Du Gonghuan,Zhu Zhemin,Gong Xiufen.Acoustics Foundation (third edition)[M].Nanjing:Nanjing University Press,2012: 183-191.

6 马大猷.现代声学理论基础(第一版)[M]北京：科学出版社，2004:10-30.

Ma Dayou.Modern Acoustic Theory (first edition)[M].Beijing:Science Press,2004:10-30.

7 Landau L D,Lifshsitz E M.Fluid Mechanics[M]. Pergamon Press,Oxford,1959,49:15.

8 Swift G W.Thermoacoustic engines and refrigerations[J].Ency-clopedia of Applied Physics,1997,21:245.

Analysis of micro thermodynamic cycle of gas in the stacks of thermoacoustic refrigerator

Wang Jianxin Kan Xiaomei Meng Nan Li Dong

( Mechanical and Engineering Institute,Inner Mongolia University of Science and Technology, Baotou 014010,China)

Based on the theory of linear small amplitude sound field, the energy transfer between the gas micro mass and the solid plate was discussed. The thermal process of the cavity plate stack was analyzed systematically.Lagrange method was adopted to study the heat exchange between the solid pack and gas mass.By analyzing the variation of the diagrams of total acoustic energy in one mass,the change in value of the heat exchange between gas micro mass and solid plate can be obsrved.The results show that different gas micro masses in the standing wave sound field, like some mini refrigerators, which cooperate with each other delicately and have complete functions. Through the relay action of gas micro mass,the heat on the plate is remored and obtained refrigerating capacity at the low temperature end is obtained.

thermoacoustic refrigerator;micro thermodynamic cycle;sound field distribution;stack;heat-transfer

2016-07-07；

2016-09-29

国家自然科学基金资助项目(No.51365033)。

汪建新，男，54岁，博士，教授。

TB61,TB66

A

1000-6516(2016)05-0022-08