行波型热声发动机的数值模拟实验

李晓明 梅宏昆 高 鹏 孔晓莉

(1辽宁科技大学材料与冶金学院 鞍山 114051)(2河北大唐国际唐山热电有限责任公司 河北 063000)

行波型热声发动机的数值模拟实验

李晓明1梅宏昆1高 鹏2孔晓莉1

(1辽宁科技大学材料与冶金学院 鞍山 114051)(2河北大唐国际唐山热电有限责任公司 河北 063000)

首次采用有限元法(FEM)，对行波型热声发动机实验系统进行了数值模拟，以线性热声理论作为计算模型，且与实验系统具有相同的几何结构和运行工况，同时采用有限元方法中的加权余量法对计算模型进行求解，通过自主编写的MATLAB计算程序，对热声系统进行一系列的迭代计算，计算结果成功观测到了行波型热声发动机系统内复杂的声场分布特性和流场特性。计算结果与实验结果的对比验证了有限元方法对行波型热声发动机模拟的有效性。

行波 热声发动机 有限元

1 引 言

热声学在理论和技术不断发展，应用这些理论和技术所指导的实验也取得了很多有意义的成果。可是由于热声系统内在机理的复杂性，目前的热声理论仅仅适用于小振幅的热声震荡[1]，并且对于热声自激振荡[2]的工作机理很难解释清楚，给热声热机的数值模拟带来很多困难。近些年来，随着计算机技术的高速发展以及有限元方法[3]自身的优越性使得其在科学和工程领域的应用较为广泛。因此，本文首次采用有限元方法对行波型热声发动机系统进行数值模拟，计算采用MATLAB仿真软件自行编写程序[4]，通过计算，得到了发动机内部的声场分布。计算结果与实验结果的对比验证了有限元法对热声发动机模拟的有效性。

2 计算模型及计算方法

2.1 物理模型

本文模拟计算的物理模型为行波热声发动机系统，如图1所示，其主要结构参数和物性参数见表1和表2。

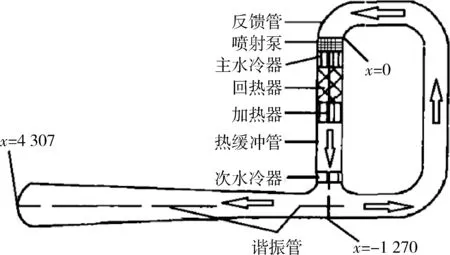
图1 行波型热声发动机实验系统示意图Fig.1 Schematic of experimental traveling-wave thermoacoustic engine

如图1所示，系统依次布置为同轴心管, 反馈管、喷射泵、主水冷器、板叠、加热器、热缓冲管、次水冷器和谐振管。反馈管末端处的坐标定为X=-1 270 mm,喷射泵处的坐标定为坐标原点X=0 mm,然后依次往左直到谐振管的末端X=4 307 mm处结束。

模拟计算采用与实际热声发动机实验系统相同的物理模型。表1给出了行波热声发动机实验系统内各部件的结构参数。表2给出了热声发动机系统内部的主要物理参数，模拟选用氦气为气体工质，平均压力为3.0 MPa。表中的物理参数除密度是通过其他状态方程计算外其他都与温度变化有关。

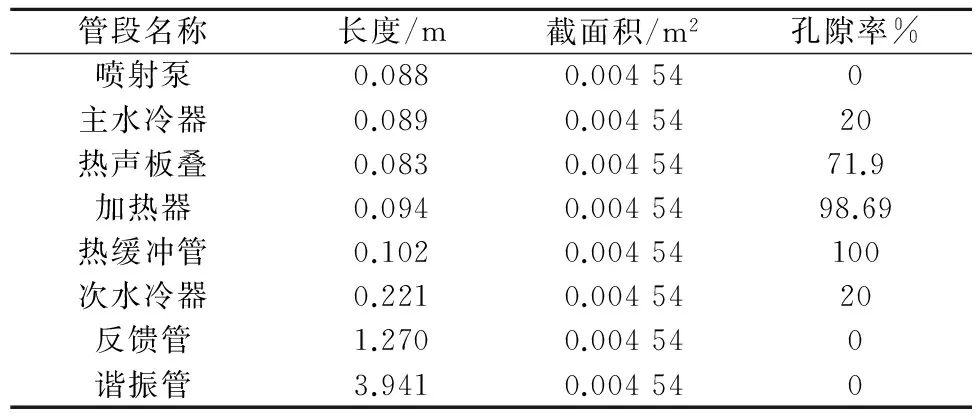
表1 行波型热声发动机的主要结构参数Table 1 Main structural parameters of the traveling-wave thermoacoustic engine

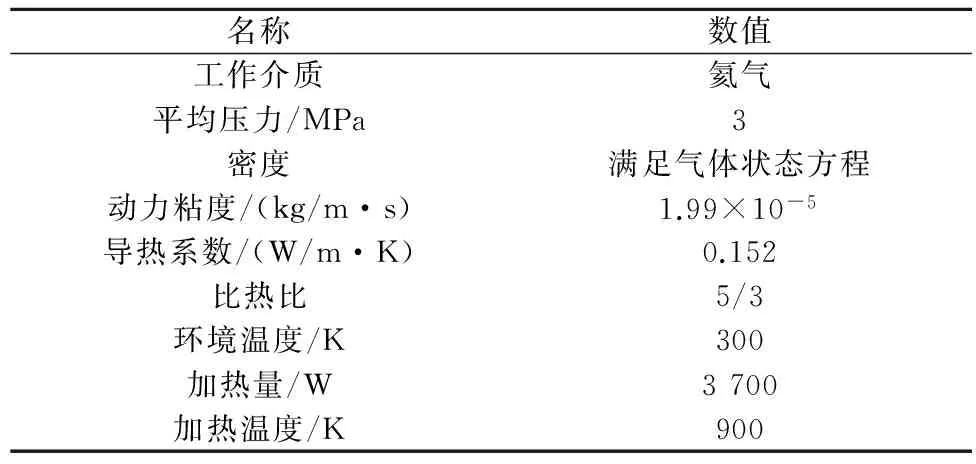
表2 行波型热声发动机的主要物理参数Table 2 Main physical parameters of the traveling-wave thermoacoustic engine

2.2 数学模型

以线性热声理论[5]作为本次模拟计算的数学模型，系统中的加热器和换热器均采用板式换热器，二者的特点是其设计的水利半径小于气体的热渗透深度和粘性渗透深度，因换热器中存在热量交换，所以数学模型中增加了时均总能流方程，且总能流的变换等于换热器的传热量。具体的数学模型如下：

压力梯度方程：

(1)

体积流率梯度方程：

(2)

温度梯度方程：

(3)

总能流方程：

(4)

声功方程：

(5)

其中：

(6)

(7)

系统中只有热声板叠和热缓冲管存在温度梯度，且只有在板叠中才能产生声功，其他的部件没有温度梯度，因此温度梯度项为零。另外，喷射泵、反馈管和谐振管的数学模型除了总能流方程为零以外，其余的都与主水冷器和次水冷器的数学模型相同。以上模型中，P1和U1表示声场中的一阶波动压力和一阶波动体积流率；负号表示共轭；i为复数符号；ω为波动角频率，rad/s；Agas为流体流道截面积，m2；ρm为流体工质的平均密度，kg/m3；Pm为平均压力，Pa；Tm为平均温度，K；γ为流体的比热比；Kgas为热导率，W/m·K；cp为定压比热，J/kg·K；σ为普朗特数；复数变量fv和fk与固体流道的几何结构有关，Asolid为固体流道的截面积，m2；Ksolid为固体热导率，W/m·K；H2为系统的总能流，W；E2为系统的声功流，W。

2.3 有限元模型

模拟采用有限元方法，对行波型热声发动机实验系统进行了数值模拟。其模型如下：

总体有限元方程：

(8)

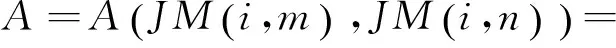
(9)

(10)

有限元总体方程为AX=B，其中A为N*N矩阵，X为N*1向量，B为N*1向量，N为总体节点数，m的变化范围是由1到JM的列数，n的变化范围是由1到JM的列数，即m和n分别对应JM(i,m)和JM(i,n)的数值。在此基础上，将边界条件JB(i,j)数据库带入总体方程，并采用对角线归一法对方程进行降阶，选用雅克比迭代计算方法对方程求解。

2.4 数值模拟计算

通过MATLAB软件利用有限元方法对热声系统进行模拟，首先对所要计算的结构区域进行网格离散，然后对上述的数学模型采用有限元方法中的伽辽金逼近建立单元刚度矩阵，根据划分的网格形式将所有的单元矩阵组合成整体刚度矩阵，加入必要的边界条件，对不同的结构输入相应初始变量和待定参数，使模型封闭，按顺序对热声系统各部件进行计算。在计算过程中，把实验系统看成是由一些相互串联的元部件所构成的整体，采用打靶法的思想，适当的猜测和调整入口边界的初始值，利用波动压力、波动体积流率和平均温度等参数的连续性来使相邻元部件之间的解满足条件，在每一个元部件中，根据部件的尺寸形状来对连续性方程、动量方程、能量方程、总能流方程进行积分,经过迭代计算，直到计算终值满足给定边界条件为止。

3 分 析

本文成功地对一台行波热声发动机进行了模拟，计算得到了发动机系统内部的声场分布情况，同时也对其各个部件包括热声板叠、加热器以及谐振管进行了系统的分析研究，其结果如下。

3.1 系统内部基本声场分析

图2、图3分别为系统内压力和体积流率振幅随热声系统位置的变化，其中-1 270 mm到0为反馈管，0到(4 307 mm)依次为喷射泵、主水冷器、回热器、加热器、热缓冲管、次水冷器、三通接头(X=680 mm)、谐振管末端。图2、图3可以看出在热声板叠的进口端出现了压力振幅的最大值，且压力振幅在热声板叠中逐渐地减小，在谐振管中达到了最小值，随后压力振幅反相逐渐增大，并且在谐振管的末端达到一个最大值。而体积流率振幅趋势与压力振幅正好相反，在热声板叠的进口端出现了体积流率振幅的最小值，由Z=P/U可知，阻抗在此处亦达到了最大值。此点的体积流率振幅并不为0，并非体积流率的节点。因此在热声板叠的进口处不可能存在体积流率的节点，体积流率的节点出现在谐振管的末端。

图2 系统内压力振幅分布Fig.2 Distribution of pressure amplitude in system

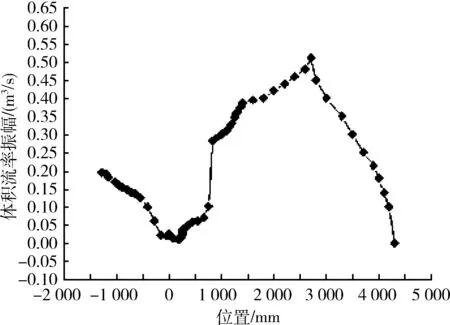
图3 系统内体积流率振幅分布Fig.3 Distribution of volume flow rateamplitude in system

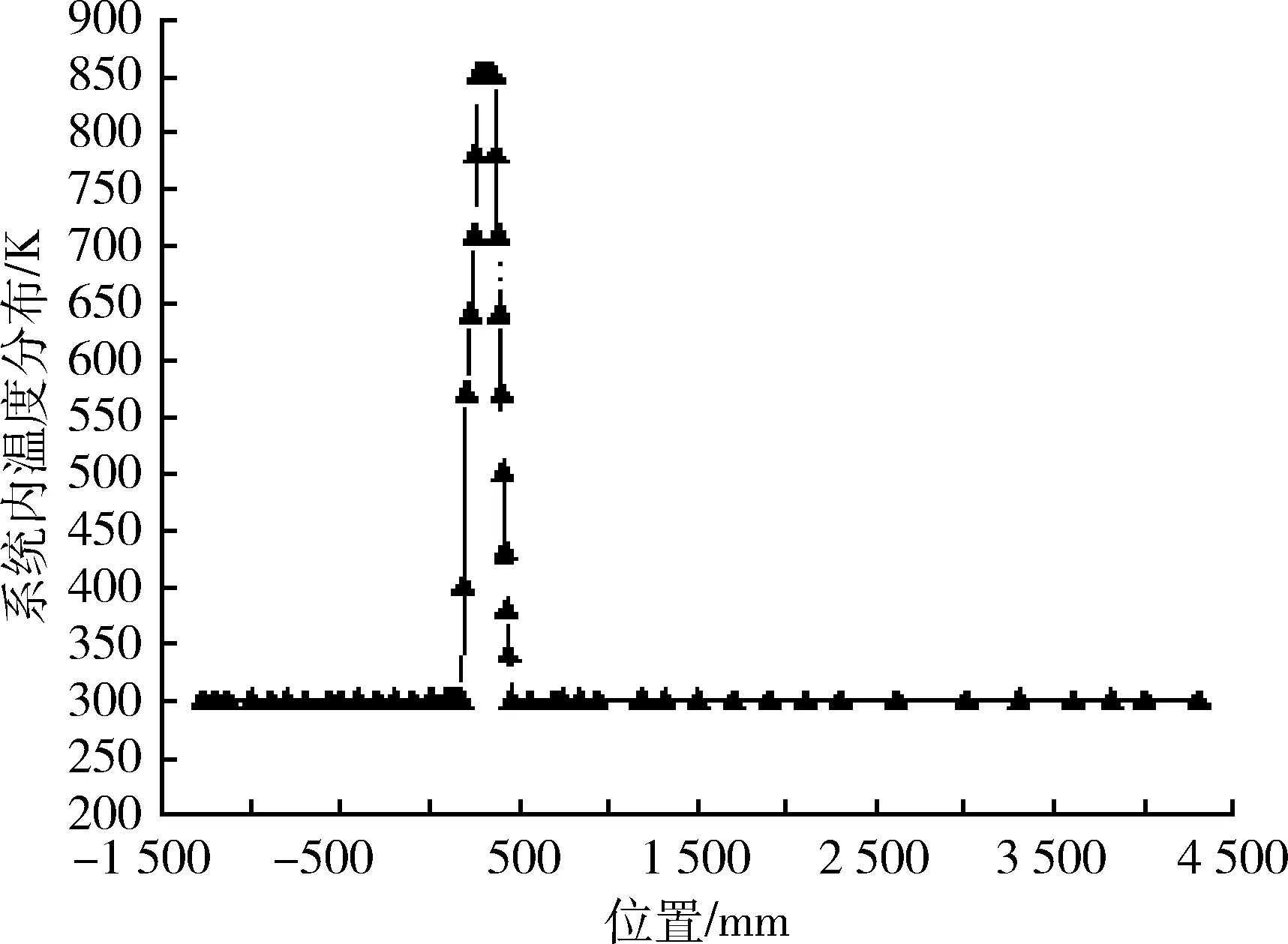
图4 系统内的温度分布图Fig.4 Temperature distribution within system

图4为系统内部温度的沿程变化，热声系统位置同图2、图3。图4可以看出，在热声板叠内随着热声板叠长度的增加，温度随之增加，加热器中的温度不变，从加热器到次水冷器之间温度逐渐下降至环境温度。在反馈管环路以及谐振管中，温度不变。在热声板叠与热缓冲管内，温度的变化最为明显。

图5为系统内声功的沿程变化，热声系统位置同图2、图3。图5可以看到，热声板叠内声功有一定幅度的增加，系统如果不接负载的情况下，产生的这些声功将会被耗散在系统管路中。还可以看到，在三通管处声功其被分配成两路，一路进入反馈管环路来维持自激振荡，另一路进入谐振管逐渐被消耗。

图5 系统内的声功分布Fig.5 Acoustic power distribution within system

3.2 各个部件模拟结果分析

图6为热声板叠内声功分布随热声位置的变化关系。从图6中发现，声功一开始是不断增加的，并且在接近热声板叠的出口约20 mm处，声功达到了最大值。然后开始逐渐地减小，这说明声功在热声板叠后面的一段并没有产生，且以前产生的声功亦被消耗了一部分，此时可以计算声功的消耗量占声功放大量的比例为28.7%。因此，要保证热声板叠内的声功一直处于增加状态，就需要再设计中保证dE2/dx>0。

图6 热声板叠内的声功分布Fig.6 Acoustic power distribution within regenerator

图7热声板叠内温度梯度和产生声功之间的关系。从图中可以看出，当其他条件保持不变时，热声板叠内产生的声功随着温度梯度的升高而增多。可以这样认为：热声板叠两端的温度梯度的增大，实际上是加热器所提供的加热功率增大了，从而导致气体从板叠吸收的热量也增加了，所以热声板叠内热能转化为声能的过程也就越发强烈，产生的声功也就越来越多。

图7 热声板叠内的温度梯度与声功的关系Fig.7 Relations between temperature gradient and acoustic power within regenerator

图9、图10为加热器内加热温度、加热功率与热声板叠内产生声功的关系。从两图中可以看出，当其他的条件不变时，热声板叠内产生的声功随着加热温度的增加而增加。输入的加热功率越高，热声板叠内产生的声功量会相应地增大。

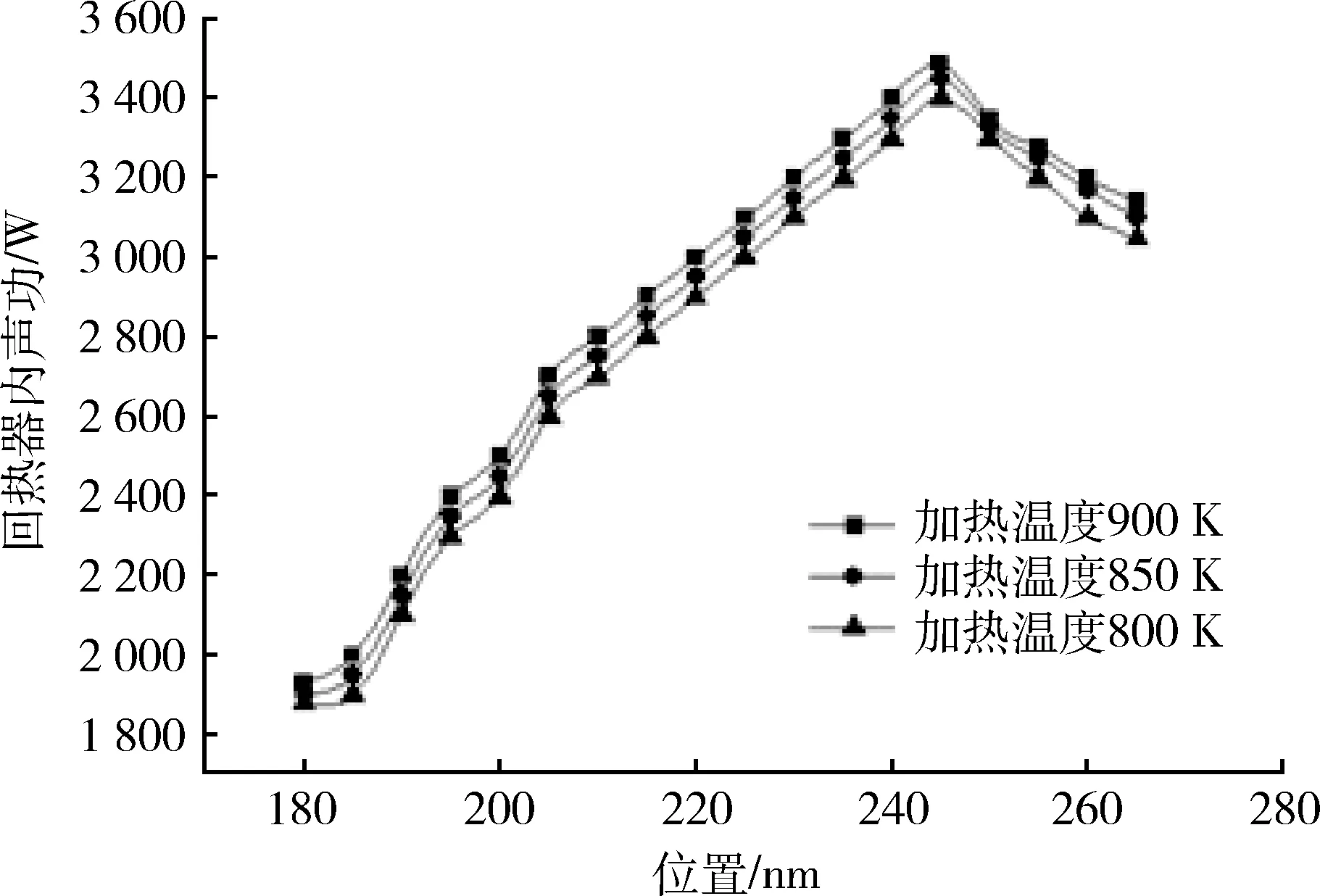
图9 加热温度与热声板叠声功的关系Fig.9 Relations between heating temperature and power of regenerator

图10 加热功率与热声板叠声功的关系Fig.10 Relations between heating power and acoustic power of regeneratoracoustic

图11、图12为系统内声功、工作频率与谐振管长度之间的关系。从前文可知，在三通管处体积流率被分为了两路，一路流向了谐振管，另一路流向了反馈管，此处的声功分配与体积流率分配一致，并且被逐渐地消耗，直到消耗殆尽，如图11所示。从图12可以发现，当谐振管的长度增加时，实验系统的工作频率会相应地降低。从进口处的106 Hz减小到了出口处的93 Hz，减幅近12%，与实验相符。

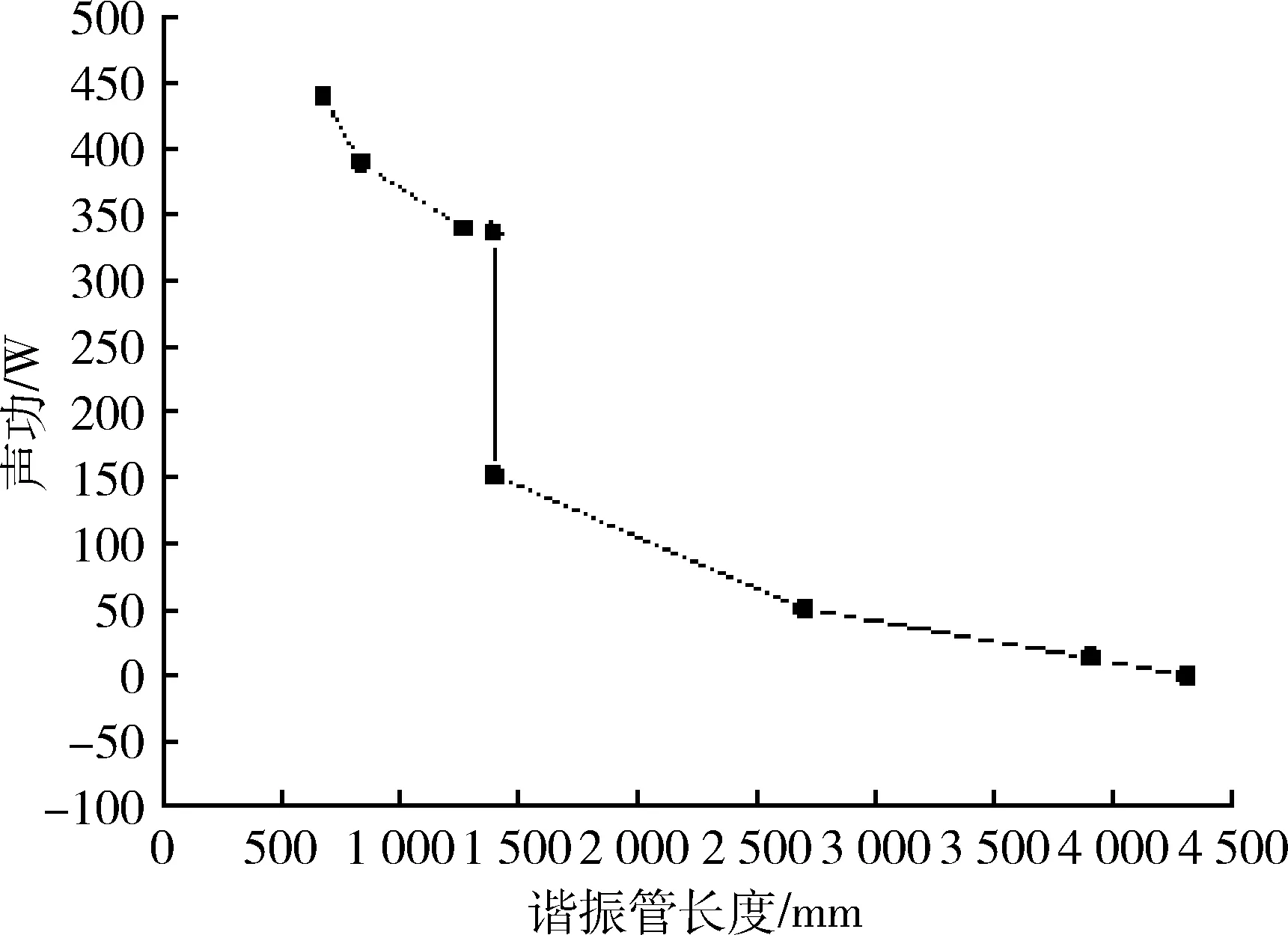
图11 谐振管内的声功分布图Fig.11 Acoustic power distribution within resonance tube

图12 谐振管的长度与工作频率的关系Fig.12 Relations between the length of resonance tube and working frequency

3.3 与实验结果的对比

为了验证模拟的准确性，将模拟结果与发动机系统中压力测点P1(三通管处)所测数据进行对比。在这里将模拟所得工作频率与压力振幅进行对比，结果列于表3中。从表中可以看出，模拟计算结果同实验结果存在一定的误差，发动机工作频率的误差在10%左右，压力振幅的误差达到了18%。产生误差原因总结为以下几点：(1)在对热声发动机的整体结构进行简化时，只是将系统中的部件简化成了直管形式，从而忽略了那些结构为锥管的部件；(2)热声系统中回热器的物理模型和数学模型还不够精确；(3)目前的热声理论不够完善，不能对系统中产生的非线性现象做出解释。

表3 计算结果与实验结果对比Table 3 Comparison between computation results and experimental results

4 结 论

采用了有限元分析方法中的加权余量法，利用MATLAB软件编程，对行波型热声发动机系统进行了数值模拟，得到了实际热声系统内工质流体的压力振幅分布、体积流率振幅分布及声功分布。依据系统内参数分布，研究得到：系统的谐振管形式介于1/4到1/2波长之间，且体积流率节点出现在谐振管的末端；热声板叠内主要为行波声场，谐振管内为驻波声场；要保证热声板叠内声功处于一直增加状态，需设计保证dE2/dx>0，同时增加加热器的加热功率、加热温度，热声板叠内的温度梯度、长度以及内部孔隙率，声功也会增加。模拟结果及与实验系统的结果对比说明了采用有限元方法对行波型热声发动机进行数值模拟并指导热声系统设计的可行性，并为进一步模拟热声系统的高维高阶模型奠定了基础。

1 Rott N. Damped and thermally driven acoustic oscillations in wide and narrow tubes[J]. Zeitschrift furAngewandte Mathematik und Physik (ZAMP),1969,20 (2):243.

2 余国瑶.热声发动机自激振荡过程以及热声转换特性研究[D].北京:中国科学院,2008.

Yu Guoyao.Study of spontaneous oscillation and thermoacoustic conversion characteristics of thermoacoustic heat engines[D].Beijing:Chinese Academy of Sciences,2008.

3 (美)G.R.布查南.全美经典有限元分析[M].北京:科学出版社,2002.

George R Buchanan. Schaum’s outline of theory and problems of finite element analysis[M].Beijing:Science Press,2002.

4 毕 超.计算流体力学有限元方法及其程序详解[M].北京：机械工业出版社,2013.7.

Bi Chao. Finite element method and programming of computation fluid dynamics[M]. China Machine Press, 2013.7.

5 肖家华.热声效应与回热式制冷机(热机)的热声理论[D].北京:中国科学院, 1990.

Xiao Jiahua. Thermoacoustic theory of thermoacoustic effect and regenerative cryogenic refrigerator[D].Bei jing: Chinese Academy of Sciences,1990.

《低温工程》关于实行参考文献中-英双语对照标注的启事

为了进一步深入报道我国低温技术所取得的最新研究成果，加强我国低温技术在国际低温学术领域的交流与影响，促进世界各国低温学者间的相互交流，本刊对刊登的稿件中引用的中文参考文献实行中-英双语对照标注。作者向本刊投稿时，请对文后所列的中文参考文献同时标注对应的英文内容。

(1)引用近些年的连续出版物、学位论文、会议论文等类中文文献，其对应的英文内容一般可直接从引用的文献中直接获取；其它类中文文献，其对应的英文内容一般需要作者自行翻译。

(2)引用的中文参考文献中-英双语对照标注方式及格式示例如下：

1 杨世铭，陶文铨. 传热学[M]. 北京：高等教育出版社，1998：324-326.

1 Yang Shiming，Tao Wenquan. Heat Transmission Science[M]. Beijing：Higher Education Press，1998：324-326.

2 丁闪，王毅，李冀鹏，等. 液氢循环预冷泵用电机的研制[J]. 低温工程，2013(6)：48-51.

2 Ding Shan，Wang Yi，Li Jipeng，et al. Development and experiment research of liquid hydrogen recirculation pre-cooling pump motor[J]. Cryogenics，2013(6)：48-51.

(3)所列的参考文献应为必须引用的必要文献，例如需要标示出重要观点、重要计算公式、重要设计依据、重要数据、重要结论来源，以对论文中的内容进行佐证或说明的。不必要的文献尽量不用，以尽可能减少版面占用。

Finite element numerical simulation of traveling-wave thermoacoustic engine

Li Xiaoming1Mei Hongkun1Gao Peng2Kong Xiaoli1

(1School of materials and metallurgy, University of Science and Technology Liaoning, Anshan 114051，China)(2Hebei Dating international Tangshan thermal power Co.,Ltd ,Hebei 063000,China)

Experimental system of a traveling-wave thermoacoustic engine has been studied by numerical simulation based on finite element method (FEM),using the linear thermoacoustic theory as the calculation model, which has the same geometrical structureand operating conditions with the experimental system. It adopts weighted residual method of the FEM to solve the calculation model,and a MATLAB calculation program to make iterative calculation of thermoacoustic system. The calculation results exhibit acoustic field distribution characteristics and complex flow field characteristics of traveling-wave thermoacoustic engine.In addition, the calculated results are compared with the experimental results.

traveling wave; thermoacoustic engine; finite element

2015-11-09；

2016-06-05

国家自然基金青年基金(项目号：51206074)

李晓明，男，39岁，博士，讲师。

TB651

A

1000-6516(2016)03-0057-06