基于马氏距离的多高斯Voronoi图生成方法
2016-06-01康顺,相诗尧
康 顺,相 诗 尧
(中国矿业大学(北京) 地球科学与测绘工程学院,北京 100083)
基于马氏距离的多高斯Voronoi图生成方法
康 顺,相 诗 尧
(中国矿业大学(北京) 地球科学与测绘工程学院,北京 100083)
Voronoi图作为一种重要的几何结构,不仅是计算几何研究的重要内容,还是地理空间分析的有力工具,在科学与工程领域应用广泛。针对传统欧氏距离条件下Voronoi图生长元权值大小等同、生长元与Voronoi图数据结构一对一关系的局限性,该文以高斯分布的统计距离为切入点,利用马氏距离作为Voronoi图生成距离测度,提出一种新的Voronoi图,即多高斯Voronoi图(MGVD)。MGVD不但囊括了欧氏距离作用下产生的普通Voronoi图与加权Voronoi图,而且将生长元与Voronoi图数据结构的一对一关系拓展为空间的一对多关系,表现出单个空间生长元的多个Voronoi图存在。最后,通过模拟实验验证了该方法的可行性。
欧氏距离;马氏距离;多高斯;Voronoi图;一对多关系
0 引言
Voronoi数据结构是一种存在于自然界的宏观和微观实体间以距离函数相互作用的普遍结构,在地理信息科学、计算机图形学、人工智能、生态学等领域具有广泛应用[1]。国外相关研究包括Aurenhammer 对Voronoi图的基本几何数据结构的研究[2];DONG、Aurenhammer等对空间点、线和面要素的加权Voronoi图算法进行的研究[3,4];Du等对质心Voronoi图的研究[5,6];Boissonnat等采用一种布雷格曼增益(Bregman divergence)的距离函数形式生成Voronoi图[7];Balzer等构建的层次Voronoi树结构图[8]等。国内主要有陈军等对Voronoi动态空间数据模型的研究,并提出了基于Voronoi图的k阶空间邻近关系、基于Voronoi空间拓扑关系的九交模型、球面Voronoi图的生成算法研究[9-12];文献[13]基于Voronoi图的GIS空间关系计算研究;文献[14]利用线性四叉树结构实现了栅格数据下Voronoi图的反向膨胀生成方法;文献[15]通过扫描线算法构建出Voronoi图;以及文献[16]由水流扩展思想生成网络Voronoi图等。
上述方法对Voronoi的发展起到了积极的推动作用,然而在Voronoi图势力范围的界定上还局限于欧氏距离或欧氏加权距离。鉴于欧氏距离对空间不确定性表达的局限性:首先,就数据本身的不确定性而言,欧氏距离未顾及空间数据的自相关性;其次,该距离条件下生长元所产生的Voronoi区域仅存在生长元作用的一定邻域范围内,数据结构表现为生长元与Voronoi图的一对一关系,无法满足由于空间分布结构而产生的跨越邻近Voronoi图而产生的空间竞争力模型,如:空间中的购物广场,鉴于其知名度所产生的“引力”不仅对周围邻近对象存在影响力,而且对邻域外的空间对象也具有一定的吸引力,在Voronoi数据结构上表现为生长元Voronoi图空间分布的离散性,呈现出生长元与其Voronoi图之间的一对多关系。基于此,本文提出了一种新的Voronoi图——多高斯Voronoi 图(Multi-Gaussian Voronoi Diagram,MGVD),以马氏距离为切入点探究Voronoi图的空间结构。
1 不确定性估计
客观世界是一个充斥着偶然性的纷乱世界,空间实体具有复杂性和可变性。观测数据远少于客观总体数据,数据的期望值通常由观测数据近似,属性的感知除实体本身外,更多是基于空间实体间的邻接关系[17]。如数据不确定性中的空间位置不确定是指空间实体的位置与其实际位置之间存在不一致性,通常表现为以统计均值作为无偏估计、以分布方差为邻域来度量其空间的分布形态;然而,欧氏距离表达的是一种确定性距离,此项则是欧氏距离所不具备的。在不确定性研究中,高斯分布是统计中最重要的概念,是推论统计的基础。空间数据点的分布很大程度上服从高斯分布。当对未知随机过程的概率分布建模时,其确定方式多是根据中心极限定理,在多次采样的样本空间中,将样本频率作为数据整体均值的无偏估计,样本方差视作整体的无偏方差,表达式如式(1),示意图如图1。
f(x)=(2π)-p/2|∑|-1/2exp{(x-μ)T∑-1(x-μ)}
(1)

图1 二元样本统计量分布Fig.1 Bi-variable statistics distribution
在时空尺度作用下,空间数据的不确定性通常是将当前尺度下获得的数据作为一种无偏估计值进行计算,如图2所示的单高斯分布。相比之下,欧氏距离局限性主要表现为:首先,它与指标的量纲息息相关,而高斯分布中的马氏距离可消除量纲;其次,欧氏距离未考虑指标间的自相关性。此外,从统计的角度,欧氏距离的使用要求一个向量的n个分量不相关且具有相同的方差,换言之,欧氏距离适用的前提条件是各坐标对欧氏距离的贡献相同,也就是权值相等且变差大小相同,在此条件下欧氏距离才适用空间区域的界定表达,否则易得出对真实地理空间的曲解,甚至错误性结论[18]。
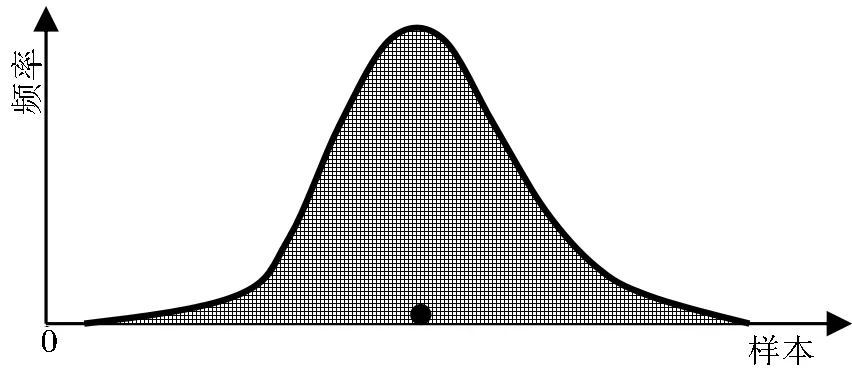
图2 一元样本统计量分布Fig.2 Sample statistics distribution of one-variable
2 多高斯Voronoi图
2.1 普通Voronoi图
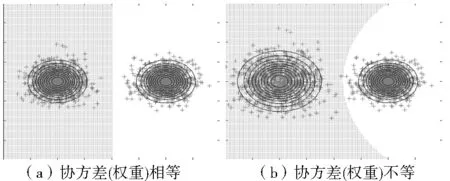
如果存在空间点集P= {x1,x2,...,xn}⊂R2,(2 V(xi)={p|d(p,xi)≤d(p,xj),j≠i,i,j∈N*} (2) 多个生长元生成的普通Voronoi图形式化表达如式(3)所示,其示例图如图3a所示;当距离函数变为加权距离d(p,xi)-wi时,则产生加权Voronoi图(WeightedVoronoiDiagram,WVD)(图3b)[8,19]。 V= {V(x1),…,V(xn)} (3) 图3 欧氏距离界定下的Voronoi图Fig.3 Voronoi diagram produced by Euclidean distances 2.2 马氏距离 欧氏距离对统计不适用性的具体表现为:当坐标表示随机波动的测量值时,需对可变性大的坐标赋予较大权值、对微小变化的坐标赋予较小权值,此时需要一个能够对距离进行不同测度表达的量值。因此,从变差及相关性角度,要求使用一种能够消除量纲、涵盖并拓展欧氏距离作用的马氏距离,描述如下: (4) 从图4可以看出欧氏距离是协方差为单位矩阵的马氏距离,即当马氏距离的协方差阵为单位阵时,马氏距离与欧氏距离是等价的。 图4 马氏距离Fig.4 Mahalanobis distance (5) 定义 多高斯Voronoi图: 若存在空间点集P= {x1,x2,…,xn}⊂R2,(2 MGV(xi)={p|dm(p,xi)≤dm(p,xj),j≠i,i,j∈N*} (6) 则多高斯Voronoi图(MGVD)的形式化表达如式(7),图形可视化表达如图5所示。 MGV= {MGV(x1),…,MGV(xn)} (7) 图5 马氏距离界定下的多高斯Voronoi图Fig.5 MGVD generated by Mahalanobis distance 该实验采用MATLAB 6.5模拟的空间分布数据为实验算例,研究了空间中存在多种高斯分布的生长元Voronoi图表现形式,如马氏距离中协方差正相关性相同、大小相等条件下的多高斯Voronoi图存在形式,即表现为普通Voronoi图;协方差正相关性相同、大小不等条件下多高斯Voronoi图存在形式,即表现为加权Voronoi图;协方差正相关、负相关性并存、大小不相等条件下多高斯Voronoi图的存在形式,即表现为一种跨域性、生长元与Voronoi图表现为一对多关系的空间结构。 图6a对应为式(8)、式(9)实验模拟生成的距离协方差正相关、数值大小相等条件下的多高斯Voronoi图表达,即普通Voronoi图。 (8) (9) 图6b对应为式(10)、式(11)实验模拟生成的距离协方差正相关、数值大小不等条件下多高斯Voronoi图存在形式,即表现为一种加权Voronoi图。 (10) (11) 图6c对应为式(12)、式(13)实验模拟生成的距离协方差正相关、负相关并存,且协方差数值大小不等条件下多高斯Voronoi图的存在形式,即表型出Voronoi图在空间分布中的一种离散型态,体现出Voronoi图的跨域性。 (12) (13) 图6 协方差矩阵不同的多高斯Voronoi图Fig.6 MGVD on different covariance matrices 上述实验表明,马氏距离生成的多高斯Voronoi图不仅可以利用距离协方差矩阵综合普通Voronoi图、加权Voronoi图的欧氏距离生成方式,而且实验生成的多高斯Voronoi图能够产生具有跨域延展性的离散Voronoi图。顾及数据本身的相关性,由图6可知,由马氏距离产生的Voronoi图空间结构可表现为普通Voronoi图、加权Voronoi图及跨域性Voronoi图。跨域性Voronoi图延展了传统Voronoi图的概念,如图6c中由左上方生长元所产生的两个Voronoi图Ⅰ跨越Voronoi图Ⅱ,形成空间离散分布形态存在的Voronoi图Ⅰ,表明其影响范围不仅仅局限于生长元自身的一定空间邻域内,而且可拓展至其Voronoi图以外的其他生长元的Voronoi邻域内,表现出Voronoi图切入到其他生长元Voronoi图之间形成竞争关系,扩展了传统Voronoi数据结构与生长元的一对一关系,实现了空间生长元与Voronoi图之间数据结构一对多关系的表达。 本文分析了普通Voronoi图与加权Voronoi图的生成距离及空间结构中数据结构关系的局限性,提出一种基于马氏距离的多高斯Voronoi图生成方法。从统计角度,马氏距离不仅包含了普通Voronoi图与加权Voronoi图生成的欧氏距离,而且拓展了Voronoi图的空间结构,形成了跨域性的Voronoi图,弥补了普通Voronoi图及加权Voronoi图的空间不可分离性,实现了生长元Voronoi图的跨域性,由传统的生长元与Voronoi图一对一的数据结构关系拓展为一对多的数据结构关系。针对空间中存在的多种分布结构,发现Voronoi图在空间分布中存在的其他形态以及对Voronoi数据结构多对多关系的研究是今后研究中需要进一步探讨和解决的问题。 [1] OKABE A,BOOTS B,SUGIHARA K,et al.Spatial Tessellation:Concepts and Applications of Voronoi Diagrams[M].Chichester:John Wiley,2000.6-11. [2] AURENHAMMER F.Voronoi diagrams——A survey of a fundamental geometric data structure[J].ACM Computing Surveys,1991,23(3):345-405. [3] DONG P.Generating and updating multiplicatively weighted Voronoi diagrams for point,line and polygon features in GIS[J].Computers & Geosciences,2008,34(4):411-421. [4] AURENHAMMER F,EDELSBRUNNER H.An optimal algorithm for constructing the weighted Voronoi diagram in the plane[J].Pattern Recognition,1984,17(2):251-257. [5] DU Q,FABER V,GUNZBURGER M.Centroidal Voronoi tessellations:Applications and algorithms[J].SIAM Review,1999,41(4):637-676. [6] JU L L,DU Q,GUNZBURGER M.Probabilistic methods for centroidal Voronoi tessellations and their parallel implementations[J].Parallel Computing,2002,28(10):1477-1500. [7] BOISSONNAT J D,NIELSEN F,NOCK R.Bregman Voronoi diagrams[J].Discrete & Computational Geometry,2010,44(2):281-307. [8] BALZER M,DEUSSEN O.Voronoi treemaps[A].IEEE Symposium on Information Visualization 2005:INFOVIS[C].New York:IEEE,2005.49-56. [9] CHEN J,LI C M,LI Z L,et al.A Voronoi-based 9-intersection model for spatial relations[J].International Journal of Geographical Information Science,2001,15(3):201-220. [10] 陈军.Voronoi动态空间数据模型[M].北京:测绘出版社,2002.20-32. [11] CHEN J,ZHAO X S,LI Z L.An algorithm for the generation of Voronoi diagrams on the sphere based on QTM[J].Photogrammetric Engineering and Remote Sensing,2003,69(1):79-89. [12] CHEN J,ZHAO R L,LI Z L.Voronoi-based k-order neighbour relations for spatial analysis[J].ISPRS Journal of Photogrammetry and Remote Sensing,2004,59(1-2):60-72. [13] 赵仁亮.基于Voronoi图的空间关系计算研究[D].湖南:中南大学,2002.30-38. [14] 李佳田,陈军,赵仁亮,等.基于线性四叉树结构的Voronoi图反向膨胀生成方法[J].测绘学报,2008,37(2):236-242. [15] HU S M,JIN L,DONGUK K,et al.A sweepline algorithm for Euclidean Voronoi diagram of circles[J].Computer Aided Design,2002,38(3):260-272. [16] 艾廷华,禹文豪.水流扩展思想的网络空间Voronoi图生成[J].测绘学报,2013,42(5):760-776. [17] SHI W Z.Principles of Modeling Uncertainties in Spatial Data and Spatial Analyses[M].CRC Press,2009.8-12. [18] MAHALANOBIS P C.On the generalized distance in statistics[J].Proceedings of the National Institute of Sciences (Calcutta),1936,2:49-55. [19] 吴立新.地理信息系统原理与算法[M].北京:科学出版社,2003.283-295. A Generating Method of Multi-Gaussian Voronoi Diagram Based on Mahalanobis Distance KANG Shun,XIANG Shi-yao (CollegeofGeoscienceandSurveyingEngineering,ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China) Voronoi diagram not only is regarded as one of the most popular data structure in computational geometry,but also an advantageous tool in geospatial analysis,and provided with extensive applications in all fields of science and engineer.In terms of the equal weight values being possessed by each generating cell of Voronoi diagram,and the one-to-one relationship data structure limitation between generating cell and its corresponding Voronoi diagram produced by traditional Euclidean distance,from viewpoint of the statistical distance of Gaussian distribution,a new Voronoi diagram,namely Multi-Gaussian Voronoi Diagram,abbr.MGVD,is proposed in this paper based on Mahalanobis distance,which is utilized as the distance measure.The MGVD includes the generalization method of ordinary Voronoi and weighted Voronoi diagram based on Euclidean distance.Moreover,the MGVD extends the data structure between generating cell and its corresponding Voronoi diagram from one-to-one relationship in space to that one-to-many,which makes the spatial existence of multi-Voronoi diagram which belongs to a single generating cell.Last but not least,the method was proved to be feasible by simulation experiments. Euclidean distance;Mahalanobis distance;multi-Gaussian;Voronoi diagram;one-to-many relationship 2015-12-10; 2016-01-24 中央高校基本科研业务费专项资金项目(2010YD06) 康顺(1987- ),男,博士研究生,主要研究方向为Voronoi建模与计算。E-mail:421347922@qq.com 10.3969/j.issn.1672-0504.2016.03.010 P208 A 1672-0504(2016)03-0049-04




3 算例与分析

4 结论
