基于RS-SVM模型的滑坡易发性评价因子选择方法研究

于 宪 煜，胡 友 健，牛 瑞 卿

(1.中国地质大学(武汉)信息工程学院，湖北 武汉 430074；2.中国地质大学(武汉)地球物理与空间信息学院，湖北 武汉 430074)

基于RS-SVM模型的滑坡易发性评价因子选择方法研究

于 宪 煜1，胡 友 健1，牛 瑞 卿2

(1.中国地质大学(武汉)信息工程学院，湖北 武汉 430074；2.中国地质大学(武汉)地球物理与空间信息学院，湖北 武汉 430074)

为提高滑坡易发性评价的精度和准确性，利用粗糙集理论和支持向量机模型进行滑坡易发性评价因子选择。以三峡库区秭归到巴东段为研究区，首先通过相关分析和主成分变换对初始滑坡评价因子进行筛减与合并，将剩余的评价因子分为控制因素和影响因素，采用粗糙集理论分别对其进行属性约简，生成核因子集。然后，利用核因子集对支持向量机模型进行训练和预测，得到滑坡易发性评价结果，其预测精度和曲线下面积分别为76.9%和0.939。最后，将两种传统的对所有滑坡评价因子一同进行筛选的方法用于该研究区的滑坡易发性评价，并将传统方法与该方法的评价结果进行比较,结果表明，该文所提出的滑坡评价因子选择方法的精度和准确性均优于传统方法。

滑坡易发性评价；评价因子筛选；粗糙集理论；支持向量机

0 引言

滑坡是一种典型的地质灾害，具有分布地区广、发生频率高、运动速度快和灾害损失大等特点，严重危害人民的生命与财产安全[1,2]。科学、准确、有效地进行滑坡灾害的预测预报，对于防灾减灾具有十分重要的意义[3]。滑坡的易发性评价是一种比较有效的滑坡灾害预测方法。

已有学者采用不同方法进行了滑坡易发性评价。韩国Lee等将人工神经网络模型(Artificial Neural Networks,ANN)引入滑坡易发性评价体系，发展了滑坡易发性评价技术[4]；Lee等利用逻辑回归模型(Logistic Regression,LR)进行滑坡易发性评价[5-8]；Yao等将支持向量机模型(Support Vector Machine,SVM)应用到滑坡易发性评价中，均取得了较好效果[9-12]。

环境因素并不是一个整体，可将其分为控制因素(静态因素)和影响因素(动态因素)两大类[13，14]：控制因素是对滑坡的发生起控制作用的地质和地貌因素，控制着滑坡发生的区域地质环境、可能的规模和滑坡类型等，这些因素在长时间内是基本稳定的；影响因素是对滑坡发生起影响作用的外部因素，其作用会影响滑坡灾害发生的时间，是动态变化的。控制因素和影响因素包括地形地貌、地质、水文、降雨、人类工程活动等多方面的数据，甚至对于某些特殊的研究区域和研究目的，滑坡体上树木的种类、平均直径、密度、树龄[15]及地面峰值加速度[16]等在滑坡研究中不常见的因素也作为参与模型构建的因子出现。因此，如何科学、合理地确定对滑坡发生起决定性作用的影响因子集，是一个非常棘手的问题，也是在许多研究中没有提及的问题[17]。

为提高滑坡易发性评价结果的精度和准确性，本文基于粗糙集理论(Rough Set,RS)和支持向量机模型进行滑坡易发性评价因子选择。以三峡库区秭归到巴东段为研究区，首先利用ArcGIS、SAGA GIS及ENVI软件从遥感影像和数字高程模型中获得初始滑坡评价因子，在利用相关性分析和主成分变换对因子进行筛减和合并后，将剩余的评价因子分为控制因素和影响因素两大类。然后，采用粗糙集理论对其分别属性约简，生成核因子集。最后，运用支持向量机模型对筛选出来的核因子集进行训练和预测，得到区域滑坡易发性评价结果，并将本文提出的环境因素筛选方法与传统的筛选方法进行比较。

1 算法简介

1.1 粗糙集

RS理论是一种能够有效分析和处理不确定、不一致和不完整信息与知识的数学工具。在RS理论中，一个知识系统可以表示为[18]:

IS=(U,A,V,f)

(1)

考虑属性的子集。每个∀B∈A都在U中产生一个不可分辨关系，定义为:

Ind(B)={(xi,xj)|(xi,xj)∈U2,∀b∈B(b(xi)=b(xj))}

(2)

其中，b(xi)表示对象xi中b的属性值。如果(xi,xj)∈Ind(B)，则对象xi和xj被认为关于属性集A的子集B是不可分辨的。关于Ind(B)的等价类称为B的基本集，对于∀xi∈U，Ind(B)的等价类可以表示为[xi]Ind(B)。

对于任意对象集合的X⊆U，属性集B⊆A，则X关于B的下近似BX，是所有真包含于X的B基本集的并，表示为:

BX={xi∈U|[xi]Ind(B)⊆X}

(3)

(4)

则X的边界区域可以定义为:

(5)

如果Bnd(X)≠0，可以认为子集是不可定义集，即粗糙集(RS)，否则子集就是可定义集。属性约简和核属性集是RS理论的两个基本概念，一个核约简属性集是集合A中的属性最小集，并且能够得到和全体属性集一样的目标分类结果。

1.2 支持向量机模型

SVM是一种机器学习方法[19]，其重要应用之一就是用来分类。假设一个线性可分离的训练向量xi(i=1,2,…,n)包含了两类yi=±1，那么SVM的目的就是寻找一个n-维超平面使得这两类尽可能分开并且有最大的分类间隔。这个n-维超平面可以简化表示为:

(6)

式中:‖w‖是w的2-范数，b是用来增加间距使得超平面不会穿过原点，xi是超平面上的点，w是垂直于超平面的向量。

在引入非负的拉格朗日乘数λi后，其成本函数可以定义为:

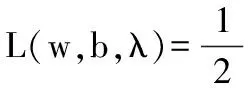
(7)

(8)

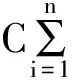
2 研究区概况与数据源

2.1 研究区概况

研究区位于长江三峡库区境内，包括巴东和秭归县，总长度约55km,地理坐标为110°18′～110°52′E，30°01′～30°56′N，面积约446km2，其地理位置如图1所示(见封2)。该地区处于中国地形三大阶梯中的第二阶梯向第三阶梯的过渡区域，是川东褶皱与鄂西山地地区的交汇处，其地貌主要特征为中低山和侵蚀峡谷。境内主要山脉是大巴山和巫山余脉，高程80～2 000m。气候属亚热带大陆性季风型气候，雨量充沛，月均降雨量为100～150mm，年均降雨量为1 100mm，降雨主要集中在春季和夏季，在这两个季节月均降雨量可达200～300mm[20]。区内基岩由前震旦纪的准晶质岩组成，有3条主要的断层和断裂带。第1条位于黄陵背斜的西南，是北北西-南南东走向的仙女山断层；第2条是北北东-南南西走向的九畹溪断层；第3条是穿过秭归盆地且与九畹溪断层有相似走向的牛口-香炉坪断裂带[21]。

2.2 数据源

本研究中，利用Landsat8卫星影像数据计算植被指数、湿度指数和建筑指数；用1∶5万比例尺地形图提取地形地貌及水体等信息；用1∶5万地质图获取地层岩性和断层信息；利用降雨和地震数据获得年均降雨量和地震震级数据；用历史滑坡存档资料和野外调查资料进行滑坡解译与滑坡空间定位。

研究区内共有滑坡202处，总面积为23.4km2，占整个研究区面积的5.89%，其中最大的滑坡是范家坪滑坡，位于长江右岸，面积达1.51km2；最小的滑坡是葵花街滑坡，面积为2 068.8m2。

3 实验方法及过程

3.1 评价因子的选取

利用ArcGIS、SAGAGIS以及ENVI等软件从遥感影像及分辨率为30m的数字高程模型中共提取58个初始评价因子，其中有23个地形地貌类因子(坡向、高程、平面曲率、剖面曲率、斜坡形态、坡度、地形粗糙指数、地形表面凸率、地形表面纹理、地形位置指数、地形地貌分类、汇聚指数、截面曲率、一般曲率、纵向曲率、切向曲率、最大曲率、最小曲率、中坡位置、总体曲率、坡长、坡高和谷深)；3个地质因子(距断层距离、岩性及斜坡结构)；13个水文因子(流域面积、流域坡度、渠网基础等级、流路长度、流宽、坡长系数、Melton崎岖系数、汇流动力指数、基于低地的地形分类指数、渠网垂直距离、地形湿度指数、流线曲率及距河网距离)；17个土地覆盖因子(归一化植被指数、归一化植被含水指数、简单比值指数、差异植被指数、大气阻抗植被指数、转换植被指数、绿色植被指数、植被覆盖度、归一化水体指数、改进的归一化水体指数、归一化水分指数、比值水分指数-1，比值水分指数-2，缨帽变换湿度指数、增强水体指数、改进的归一化建筑指数及城市土地利用指数)。此外，还有研究区的年平均降雨量因子以及地震活动因子。

3.2 划分模型计算单元和选择模型训练样本集

模型计算单元的划分方式对模型的建立和模型精度影响很大，一般可分为栅格单元、地形单元、唯一条件单元、斜坡单元和地貌单元[22]。本文采用栅格单元作为模型的计算单元，由于所用的Landsat8遥感影像数据的空间分辨率为30m，故以30m×30m作为一个栅格单元，将所有获取的评价因子重采样为30m。这样，将研究区划分为439 646个模型计算单元，其中滑坡有25 897个模型计算单元。

在样本选择中，采用移动窗口采样规则可在一定程度上消除由于空间位置导致的因子空间相关性。按照3×3窗口(90m×90m)对滑坡区域进行样本点采样，共得到3 197个滑坡样本点。由于采用SVM模型在模型训练时对训练样本集的样本均衡性有严格要求，因此，将滑坡区域以100m做缓冲区，其以外的研究区作为非滑坡区域，在非滑坡区域内随机选择和滑坡样本数相同的3 197个点作为非滑坡样本点。最后，将滑坡样本点和非滑坡样本点合并成最终的训练样本集。

3.3 评价因子的筛选

在上述58个初始评价因子中，因子之间存在一定的相关性，需要对其进行相关性分析和处理，以消除冗余。首先通过相关性分析，将地形地貌因子中的切线曲率、地形粗糙指数、流域坡度、流域面积、流路长度、基于低地的地形分类指数、地形地貌分类和汇聚指数共8个因子去掉。由于在地形地貌因子中出现了一个由7个因子组成的因子组合，其中的每个因子都与其他6个因子存在较高的相关性，故再通过主成分分析，将坡面曲率、地形位置指数、截面曲率、一般曲率、纵向曲率、最大曲率和最小曲率这7个因子转换成曲率综合第一到第七主成分(Curvature_PCA1到Curvature_PCA7)，选择第一到第三主成分作为新的评价因子(包含原始7个因子92.74%的信息)。在17个土地覆盖因子中，植被指数之间、水体指数之间和建筑指数之间有很高的相关性，也通过主成分分析，将其转换成植被综合(PCA_VI1到PCA_VI8)、水体综合(PCA_WI1到PCA_WI7)以及建筑综合(PCA_BI1，PCA_BI2)，挑选这3个综合指数的第一主成分(分别占各自指数总信息的93.7%，92.22%和98.75%)作为新的评价因子。对于13个水文因子，由于不存在由多个具有较高相关性的因子组成的因子组合，故未进行主成分分析，而是从相关性较高的因子中直接删除流域面积、流域坡度、流路长度、低地地形分类指数这4个因子，达到消除相关性的目的。

经过上述步骤，还剩余32个评价因子。采用如下3种不同方法分别进行因子筛选，以便对其筛选结果进行比较。第1种方法为常规做法，将这32个评价因子输入到Rosetta软件中得到最终的核因子集。第2种方法是将控制因素和影响因素分开，分别获得核因子集并合并为最终评价因子。第3种方法是在常规做法中，通过调整阈值来扩充核因子集中的因子数量，使其与第2种方法获取的评价因子个数相同(经过反复实验和计算，在Rosetta软件中将阈值调整为0.45即可)。本文将这3种方法分别称为基于默认阈值和传统因子筛选方法的RS-SVM模型(DT_12，对应第1种方法)、基于变化阈值和传统因子筛选方法的RS-SVM模型(T0.45_20，对应第3种方法)和基于默认阈值与本文提出的对滑坡控制因素和影响因素分别约简后再合并的因子筛选方法的RS-SVM模型(DS_20，对应第2种方法)。三种方法最终所选取的因子如表1所列。

从表1可见，通过上述3种方法获取的核因子集，无论是在因子的数量上还是在因子本身的选择上都不尽相同。DT_12中获取了12个因子作为核因子集，而T0.45_20和DS_20都获取了20个因子作为核因子集；T0.45_20因为是DT_12阈值调整后的结果，所以T0.45_20不仅包含了DT_12的所有因子，还将一部分DT_12中删减掉的因子加入了核因子集中，但是与DS_20相比，差异非常明显：在DT_12中，传统的被认为与滑坡相关性较强的因子如坡度、地形表面纹理、距河网距离等因子都被剔除在外，虽然在T0.45_20中将这些因子又加入了核因子集中，但是仍然有许多与滑坡有较强相关性的因子没有被考虑在内，如斜坡形态、岩性、地震活动、年平均降雨量等，这些因子都在DS_20中得到了体现。出现这种现象，是由于控制因素的因子和影响因素的因子之间存在着量纲以及属性等多方面的差异，将这两类因子放在一起进行核因子集的筛选，有可能造成不同类别因子在核因子集筛选中的不均衡性，造成重要的滑坡评价因子的缺失，从而影响滑坡易发性评价结果的准确性。

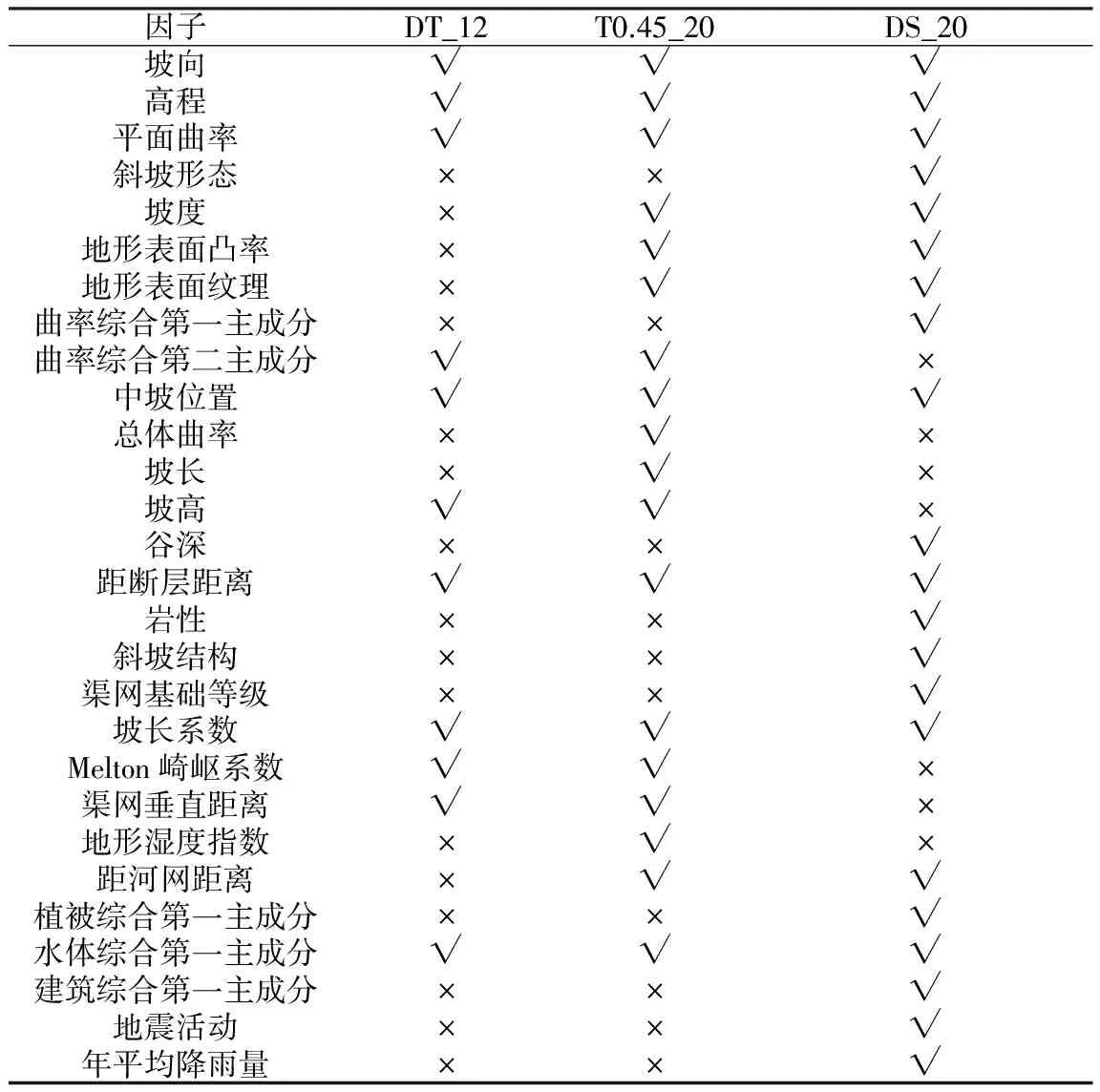
表1 三种不同方法最终选择的影响因子Table 1 The influence factors selected by the three different methods

3.4 SVM模型参数计算和滑坡易发性评价

将前述3种方法选择的核因子集提取到训练样本集中，并利用这3个训练样本集分别对SVM模型进行训练，从而得到与这3种方法对应的SVM模型参数。然后，将已经训练好的SVM模型对研究区内所有的计算单元进行预测。由于选择的SVM模型的计算结果除了分类结果之外，还同时输出属于各分类结果的概率值。最后，利用ArcGIS软件结合概率值生成滑坡易发性评价结果，即滑坡敏感性制图(Landslide Susceptibility Mapping,LSM)。

4 结果与分析

通过模型计算，可得到DT_12、T0.45_20和DS_20这3种方法的滑坡敏感性制图。为了增加滑坡敏感性制图的可读性，并且评价这3种方法的预测准确性，利用自然断点法将连续型的滑坡敏感性指数分成5个离散型的分类值，分别对应不易发区、低易发区、中易发区、高易发区和极高易发区，从而得到滑坡敏感性区划图(图2,见封2)，各区所占面积比见表2。其中，DT_12的极高易发区占滑坡面积的28%，T0.45_20的极高易发区占滑坡面积的52.5%，DS_20的极高易发区占滑坡面积的53.4%。虽然在极高易发区的区间中，本文提出的方法(DS_20)略逊于以0.45为阈值的传统因子筛选方法(T0.45_20)，但如果将高易发区和极高易发区作为危险区来考虑，DS_20的危险区占滑坡面积的76.9%，而T0.45_20的危险区仅占滑坡面积的72.8%。

表2 基于自然断点法的滑坡敏感性区划各分区所占研究区面积和滑坡面积比例Table 2 The ratio of the area of each division to the total study area and landslide area

利用滑坡敏感性区划验证了模型的预测精度，再利用ROC曲线(Receiver Operating Characteristic Curve)检验模型的预测性能。ROC曲线是反映敏感性和特异性连续变量的综合指标，并用构图法揭示敏感性和特异性的相互关系。在ROC曲线上，最靠近坐标图左上方的点为敏感性和特异性均较高的临界值。将DT_12、T0.45_20和DS_20这3种滑坡预测模型的滑坡敏感性预测值和已发生滑坡的真实值联合绘制出ROC曲线(图3)，并求得曲线下的面积AUC(Area Under the Curve)(表3)。从图3可见，DS_20的曲线在ROC曲线图中更接近左上角，而T0.45_20的曲线与左上角靠近程度要稍次于前者，DT_20与左上角距离最远。同时，表3显示，DS_20的AUC值为0.939，稍优于T0.45_20的AUC值(0.932)，但是前两者的结果都要好于DT_12的AUC值(0.912)。所以，在模型预测性能方面，本文提出的方法也优于其他两种方法。

从研究区内部分区域的滑坡分布来看，三种方法计算生成的滑坡敏感性制图结果都能得到滑坡的大致空间位置，但是DS_20无论是从滑坡空间范围预测的准确性上还是非滑坡区域的误分率上都要比T0.45_20和DT_12好得多。特别是在位于巴东县城以东的长江右岸区域，在历史资料和野外踏勘中均没有滑坡的发生或者可能生成滑坡的区域，这与DS_20的预测结果相符，而T0.45_20和DT_12却均在此处预测有大面积的高易发区和极高易发区，与实际情况不符。由此可见，本文提出的方法在模型预测的实际检验中也要优于其他两种方法。

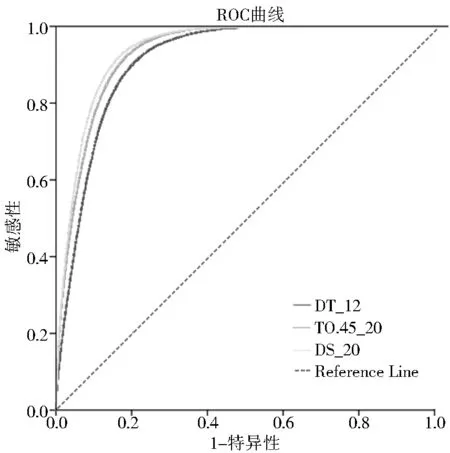
图3 DT_12、T0 45_20和DS_20三种方法的ROC曲线Fig.3 The ROC curves of the three methods

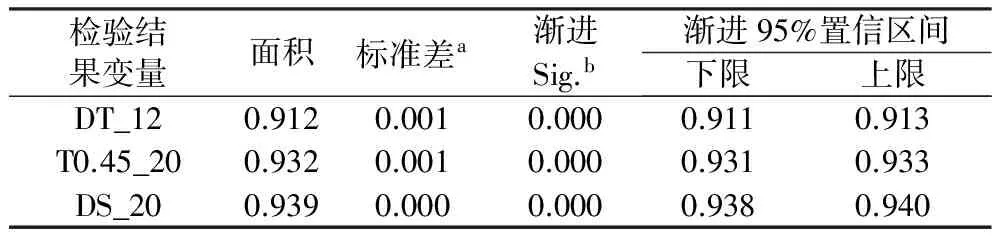
表3 曲线下面积Table 3 Area under the curve

注：a 在非参数假设下；b 零假设:实面积= 0.5。

5 结语

传统的滑坡因子筛选方法没有将滑坡影响因素分为控制因素和影响因素分别进行筛选，而是将这两类因子放在一起进行核因子集的筛选，由于控制因子与影响因子之间存在着量纲以及属性等多方面的差异，就存在不同类别的因子在核因子集筛选中的不均衡性，可能造成重要滑坡评价因子的缺失，从而影响滑坡易发性评价结果的精度和准确性。本文首先通过相关性分析和主成分变换将初始滑坡评价因子进行筛减和合并之后，将剩余的滑坡影响因素分为控制因素和影响因素两大类，再利用粗糙集理论分别对控制因素和影响因素进行属性约简，得到相应的核因子集。然后，运用支持向量机模型对筛选出来的核因子集进行训练和预测，得到滑坡易发性评价结果。这样，不仅消除了原始因子中的冗余因子，而且通过筛选能够得到对滑坡的发生起到重要作用的因子集，因而可以提高滑坡易发性评价结果的精度和准确性。实验和实际验证结果均表明，本文提出的滑坡易发性评价因子选择方法的预测精度和准确性均优于传统方法，具有较好的实用价值。

[1] 陈剑，杨志法，刘衢秋.滑坡的易滑度分区及概率预报模式[J].岩石力学与工程学报，2005，24(13)： 2392-2396.

[2] 戴福初，李军.暴雨滑坡泥石流的研究进展与趋向[J].地理研究，1998，17(增)：117-124.

[3] 牛瑞卿，彭令，叶润青，等.基于粗糙集的支持向量机滑坡易发性评价[J].吉林大学学报(地球科学版)，2012(2)：430-439.

[4] LEE S,RYU J H,MIN K,et al.Landslide susceptibility analysis using GIS and artificial neural network[J].Earth Surface Processes and Landforms,2003,28:1361-1376.

[5] LEE S,MIN K.Statistical analysis of landslide susceptibility at Yongin,Korea[J].Environmental Geology,2001,40:1095-1113.

[6] DAI F C,LEE C F.Landslide characteristics and slope instability modeling using GIS Lantau Island,Hong Kong[J].Geomorphology,2002,42:213-238.

[7] OHLMACHER C G,DAVIS C J.Using multiple regression and GIS technology to predict landslide hazard in northeast Kansas,USA[J].Engineering Geology,2003,69:331-343.

[8] AYALEW L,YAMAGISHI H.The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains,Central Japan[J].Geomorphology,2005,65:15-31.

[9] YAO X,THAM L,DA F C.Landslide susceptibility mapping based on Support Vector Machine:A case study on natural slopes of Hong Kong,China[J].Geomorphology,2008,101(4):572-582.

[10] MARJANOVI M,KOVA EVI M,BAJAT B,et al.Landslide susceptibility assessment using SVM machine learning algorithm[J].Engineering Geology,2011,123(3):225-234.

[11] BALLABIO C,STERLACCHINI S.Support vector machines for landslide susceptibility mapping:The Staffora river basin case study,Italy[J].Mathematical Geosciences,2012,44(1):47-70.

[12] XU C,DAI F C,XU X W,et al.GIS-based support vector machine modeling of earthquake-triggered landslide susceptibility in the Jianjiang River watershed,China[J].Geomorphology,2012,145:70-80.

[13] 晏同珍，杨安顺，方云.滑坡学[M].武汉：中国地质大出版社，2000.

[14] 殷坤龙，张桂荣，陈丽霞，等.滑坡灾害风险分析[M].北京：科学出版社，2010.

[15] LEE S,SONG K Y,OH H J,et al.Detection of landslides using web-based aerial photographs and landslide susceptibility mapping using geospatial analysis[J].International Journal of Remote Sensing,2012,33(16):4937-4966.

[16] LIU L,XU C,XU X,et al.Interactive statistical analysis of predisposing factors for earthquake-triggered landslides:A case study of the 2013 Lushan,China Ms7.0 earthquake[J].Environmental Earth Sciences,2015,73(8):4729-4738.

[17] 汪华斌，吴树仁，汪微波.滑坡灾害空间智能预测展望[J].地质科技情报，2008，27(2)：17-20.

[18] PAWLAK Z L A.Rough sets[J].International Journal of Computer & Information Sciences,1982,11(5):341-356.

[19] VAPNIK V.The Nature of Statistical Learning Theory[M].Springer Science & Business Media,2013.

[20] HE K Q,LI X R,YAN X Q,et al.The landslides in the Three Gorges Reservoir Region,China and the effects of water storage and rain on their stability[J].Environmental Geology,2008,55(1):55-63.

[21] LIU J G,MASON P J,CLERICI N,et al.Landslide hazard assessment in the Three Gorges area of the Yangtze river using ASTER imagery:Zigui-Badong[J].Geomorphology,2004,61(1):171-187.

[22] GUZZETTI F,CARRARA A,CARDINALI M,et al.Landslide hazard evaluation:A review of current techniques and their application in a multi-scale study,Central Italy[J].Geomorphology,1999,31(1):181-216.

Research on the Method to Select Landslide Susceptibility Evaluation Factors Based on RS-SVM Model

YU Xian-yu1，HU You-jian1，NIU Rui-qing2

(1.FacultyofInformationEngineering，ChinaUniversityofGeosciences,Wuhan430074；2.InstituteofGeophysicsandGeomatics，ChinaUniversityofGeosciences,Wuhan430074,China)

The evaluation of regional landslide susceptibility is very important for the medium and long-term prediction and forecast of the landslide hazard.Whether the evaluation results are in line with the actual situation depends on the scientific and reasonable determination of evaluation factors.In order to improve the precision and accuracy of evaluation result,this paper proposed a method to select evaluation factors of landslide susceptibility based on Rough Set theory (RS) and Support Vector Machine model (SVM).Zigui to Badong section in the Three Gorges Reservoir Area is used as a study area.Firstly,the original evaluation factors obtained from remote sensing image and digital elevation model are screened and combined by correlation analysis and Principal Components Analysis (PCA).The remaining evaluation factors were divided into control factors and influence factors,and attribute reduction is carried out on the control factors and the influencing factors by RS respectively to generate core factor set.Then,SVM model is used to train and predict the core factor set selected to get the results of the regional landslide susceptibility evaluation,the precision and accuracy of which are 76.9% and 0.939 respectively.In order to make a comparison between the proposed method to select valuation factor and those traditional ones which screen all environmental factors at the same time,the existing two traditional methods are also used for the landslide susceptibility evaluation in this study area,and the precision and accuracy of which are 53.6%,0.912 and 72.8%,0.932 respectively.The results show that the proposed method to select landslide susceptibility evaluation factors in this paper is better than the traditional methods.

landslide susceptibility evaluation;evaluation factor selection;rough set theory;support vector machine

2015-12-18；

2016-02-12

国家863项目“重大工程地质灾害快速监测与评估”(2012AA121303)

于宪煜(1987-)，男，博士研究生，主要研究方向为地质灾害监测与预测。E-mail：yuxianyu1987@126.com

10.3969/j.issn.1672-0504.2016.03.005

P642.22

A

1672-0504(2016)03-0023-06