时间序列分析在财政收入预测中的应用

许 楠

时间序列分析在财政收入预测中的应用

许 楠

介绍求和自回归移动平均模型ARIMA(p,d,q)的建模方法。将ARIMA模型应用于我国财政收入的分析与预测，结果表明ARIMA是一种短期预测精度较高的预测模型。

ARIMA模型；财政收入；预测

对财政收入进行定量分析并做出预测，可以为相关部门或者企业制定发展规划、实施相关措施提供理论参考。因此，建立准确有效的预测模型，进行时间序列分析，将有助于相关部门制定合理的财政预算，加强政府对经济的调控能力[1]。本文介绍时间序列分析的基本理论及其进展，并利用ARIMA模型对我国财政收入进行分析与预测。

一、ARIMA模型的结构

早期的时间序列分析采用Persons提出的方法，将一个时间序列分为长期趋势、循环变动、季节变动和随机变动[2]。到了1970年后，学者们不再将一个时间序列分为不同的成分，而是作为一个整体来研究，将模型分为3种：自回归模型(AR)、移动平均模型(MA)和自回归移动平均模型(ARMA)[3]。求和自回归移动平均模型(ARIMA)主要是对平稳序列建模，对非平稳序列进行平稳化后，即可按照ARMA模型的方法建立。模型结构如下：

其中：▽d=(1-B)d,B为后移算子，Bxt=xt-1,▽为差分算子，▽=(1-B),d为差分阶数；

Φ(B)=1-φ1B-…φpBp，为平稳可逆ARMA(p,q)模型的自回归系数多项式；

Θ(B)=1-θ1B-…θqBq，为平稳可逆ARMA(p,q)模型的移动平滑系数多项式；

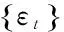
二、ARIMA建模思想

将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值[4、5]。本文利用现代统计方法、计量经济模型在某种程度上能够对我国财政收入进行预测。

三、ARIMA模型预测的基本步骤

(一)获取数据

用观测、调查、统计、抽样等方法取得被观测系统时间序列动态数据。

(二)时间序列的预处理

根据时间序列的散点图、自相关函数和偏自相关函数图，或用ADF单位根检验对序列的平稳性进行识别[6]。

这一段音乐的旋律，也是“五声性”最为明显的段落。旋律中隐含着江南水乡的明丽欢快和三月桃花烟带雨的钱塘。第三乐段（C）转入降D大调（五个降号），圆舞曲的风格更加明显，音乐轻灵流丽。第四乐段（D）转入降A大调（四个降号），歌舞更加欢畅。第四乐段结束时，音乐从头开始反复第一乐段和第二乐段，并直接连接到第5小节的短小“结尾”（Coda），在活泼、欢快、热烈中结束了全曲。

(三)模型识别

若平稳的时间序列的自相关函数拖尾,而偏相关函数是截尾的,则可断定此序列适合AR(p)模型；若平稳的时间序列的自相关函数是截尾,而偏相关函数是拖尾的,则可断定此序列适合MA(q)模型；若平稳的时间序列的自相关函数和偏自相关函数都是拖尾的,则此序列适合ARIMA(p,d,q)模型。

(四)估计模型中未知参数的值

一是检验模型参数的估计值是否具有显著性；二是检验残差序列的随机性。

(五)模型优化

如果拟合模型通过检验,仍然转向步骤3.2，则应充分考虑各种可能建立的多个拟合模型, 从所有通过检验的拟合模型中选择最优模型[7]。检验的方法主要有DF检验、ADF检验等。本文采用ADF检验方法。

(六)预测

利用拟合的ARIMA(p,d,q)模型对序列进行预测,得出预测误差。若预测误差较小, 就可以考虑接受该模型。

四、ARIMA法对我国财政收入进行建模

从中国统计局网站找到我国1985-2006年财政收入的数据，其中采用1985年至2004年的数据拟合模型，并预测2005年和2006年的数据，见表1。

表1 中国1985-2006年财政收入总额表(单位：亿元)

第一步，将财政收入用序列xt表示，用1985-2004年的序列xt做时序图，用后两年数据做模型预测检验。从图1可以看出，该时序图前后趋势波动不同，并向右上方倾斜，说明序列存在一定的增长趋势，同时存在异方差。该序列不是平稳序列，需要进行平稳化处理。

图1 我国财政收入时序图(1985-2004年)

第二步，平稳化处理。首先对序列xt取自然对数，序列变为logxt，记为Zt。再对Zt一阶差分，消除趋势性，取对数差分后序列利用自相关图和偏相关图及单位根检验来确定序列Zt的平稳性和白噪声。如图2-5所示。

图2 时序自相关和偏自相关图

t-StatisticProb.AugmentedDickey-Fullerteststatistic-4.3215480.0042Testcriticalvalues:1%level-3.8867515%level-3.05316910%level-2.666593

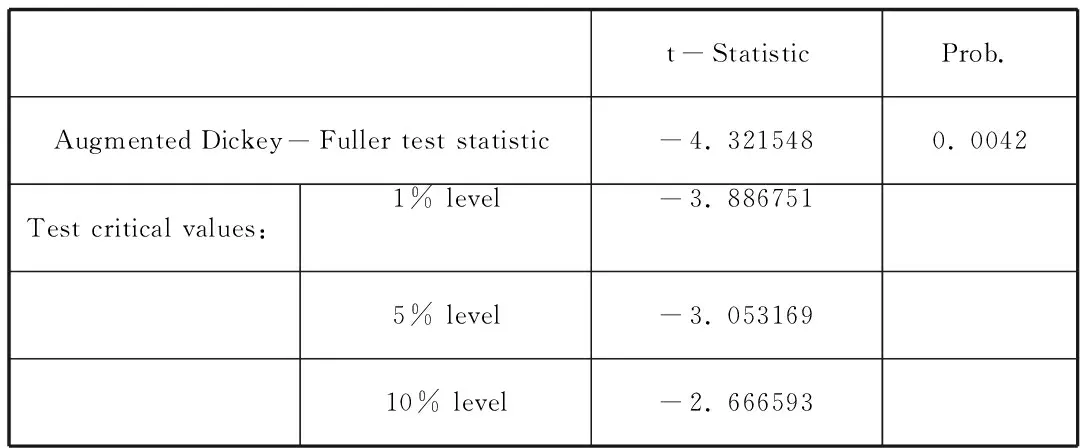
图3 一阶差分ADF检验

从自相关图看，除了延迟1阶、2阶和3阶的自相关系数大于两倍标准外，其他的都在两倍标准差内，说明该序列具有短期相关性，由图3的ADF检验知，该序列α=0.01水平下平稳。经分析可知该序列为平稳非白噪声序列，可以对其进行建模。

第三步，模型识别及参数估计和模型优化。由自相关图和偏相关图可知，除延迟1阶的偏自相关系数大于两倍标准外，其他的都在两倍标准差，是拖尾的，适合建立ARMIA(p,d,q)模型。经过反复尝试及拟合，发现模型ARIMA(2,1,1)比较合适，参数显著性如图 4，残差序列的随机性检验如图5。

图4ARIMA(2,1,1)回归结果

图5 残差序列相关性检验

可以看出，残差不存在自相关，说明模型ARIMA(2,1,1)的拟合度较高。

图6 模型建立结果

第四步，预测检验。本研究预测的是对数数据值，因此，要想得到原始数据的预测值，必须要将对数值的预测变换回原来的预测单位。现在对进行2005-2006年的预测，并将预测值与实际值进行比较，如表2所示。

表2 预测对比图(单位：亿元)

从表2可以看出，预测值和实际值的差异较小，说明模型的预测效果较好。

五、小结

在解决一个实际问题时，确定一个合理的模型和方法对解决问题有很大的帮助。本研究利用ARIMA模型和EVIEWS软件，对我国财政收入时间序列进行预测分析。随着人们要求对实际问题讨论越来越精确，使得在实际预测工作中，采用时变参数模型和自适应预测技术的现代时间序列方法成为必然，出于研究不同变量间动态关系的需要以及计算机硬件的发展，多元模型在向量ARIMA模型中或在状态空间模型中的应用也会日益增加。(作者单位：华南理工大学经济与贸易学院)

[1] 李娜,薛俊强.基于最优ARIMA模型的我国GDP增长预测[J].统计与决策,2013(5):23-26.

[2]JonathanD.Cryer,Kung-SikChan. 时间序列分析及应用[M].北京:机械工业出版社, 2011:63-70.

[3] 高铁梅等.计量经济分析方法与建模[M].北京:清华大学出版社,2012:164-177.

[4] 侯成琪,徐绪松.计量经济学方法之时间序列分析[J].技术经济,2010(8):51-58.

[5] 罗芳琼,吴春梅.时间序列分析的理论与应用综述[J].柳州师专学报,2009(3):113-117.

[6] 郑鹏辉,单锐,陈静.时间序列分析在我国财政收入预测中的应用[J].重庆文理学院学报,2008(2):15-18.

[7] 欧阳昕.基于时间序列ARIMA模型的人民币汇率走势预测[J].现代经济信息,2011(1):224-225.

许楠(1992-)，女，江西余干人，华南理工大学经济与贸易学院硕士研究生，研究方向：经济系统决策与分析。