依托多种形式 建立数的概念

居海霞

摘 要：数的概念是学生认识和理解数学的开始，理解数的意义伴随着学生学习数学的过程。利用直观材料、借助多种模型、设计变式练习，都可以帮助学生建立清晰的数的概念，理解数的意义。

关键词：数的概念；直观材料；模型；变式练习

【中图分类号】G 【文献标识码】B 【文章编号】1008-1216（2016）05B-0089-01

面对数的认识这一重要内容，我们怎样帮助学生建立清晰的数的概念呢？笔者拟从以下三方面对小学数学整数认识进行阐述。

一、利用直观材料，培养学生数感

《义务教育数学课程标准》强调：“要引导学生联系身边具体、有趣的事物，通过观察、操作、解决问题等丰富的活动，感受数的意义。”小学生的年龄特征决定了他们正处于认知结构发展的初期，这时的数学生长需要直观材料和学生的感性认知做强力支撑。

比如，教学认识“100”，教师首先出示糖葫芦图。10串糖葫芦，一串10个，一共有多少个？糖葫芦是学生熟悉的食品，比较容易激发学生的学习兴趣。把10串整体进行出示，学生在直观图的视觉冲击下，能形象地感知“100”的多少。接着，教师出示一叠纸杯：“估一估，这里可能是多少个纸杯？”学生很容易想到会是100个纸杯。那是不是100个呢？需要数一数。怎样数，才能一眼看出是不是100个？需要10个一叠，10个一叠地摆一摆。这样，先估一估，再摆一摆，学生从中不但能进一步感知“100”的多少，而且自主建立“10个10是100”的概念。

数来源于数，量产生于量。吴正宪老师指出：“数的认识关键是要培养学生的数感，而数感是在具体的情境中培养出来的。”所以，教学中，教师要给学生提供充分的感性认识的材料，培养学生数感。

二、借助多种模型，建构数的组成

在数的认识知识板块，计数器、方格图、数位顺序表等模型，是帮助学生理解数的概念、建构数的组成的有力助手。比如，教学认识几十几的数，教师利用百数方格图帮助学生建构数的组成（如图1）。教师先让学生捧出一捧棋子，在方格里摆一摆，数一数一共有多少颗。学生在摆的过程中，感悟出“2个十和6个一合起来是26”。接着，组织学生继续向后摆数，当摆出29时，学生发现，再摆1颗，就是3个十，也就是30。学生在操作中突破“拐弯数”的难点。

数无形时少直觉，形无数时难入微。借助模型，数形结合，能帮助学生建构数的组成。

三、设计变式练习，把握核心概念

郑毓信教授指出：“尽管我们的学生在各种考核中往往都能准确和迅速地说出已学过的各个数学概念的严格定义，但如果要求他们对这些概念给出若干实例却又往往表现出极大的困难。”这就要求学生掌握数的核心概念，比如数位、计数单位、位值制等。教学中，可以通过变式练习，帮助学生强化核心概念的认识。

比如，学生认识十几时，第一个接触的应是“11”这个数。课中，为了帮助学生区分“11”两个数位上的“1”表示的不同的意义，教师采用数形结合的方法（如图2），先组织学生用小棒摆出“11”这个数，在此基础上，追问：“十位上的1是怎么摆出来的？个位上的1指什么？”通过直观演示、比较、辨析等一连串研究，学生就能清楚地认识到十位上的“1”表示1个十，个位上的“1”表示1个1，这两个1表示的意义不一样。进而，研究12、13、14等表示十几的数。下图中的练习与其相得益彰。在计数器上拨1个珠，如果这个珠在个位上，则表示1个1，如果这个珠在十位上，则表示1个十。同样，如果这个珠在百位上，则表示1个百。深层次的理解，为后续学习奠定基础。

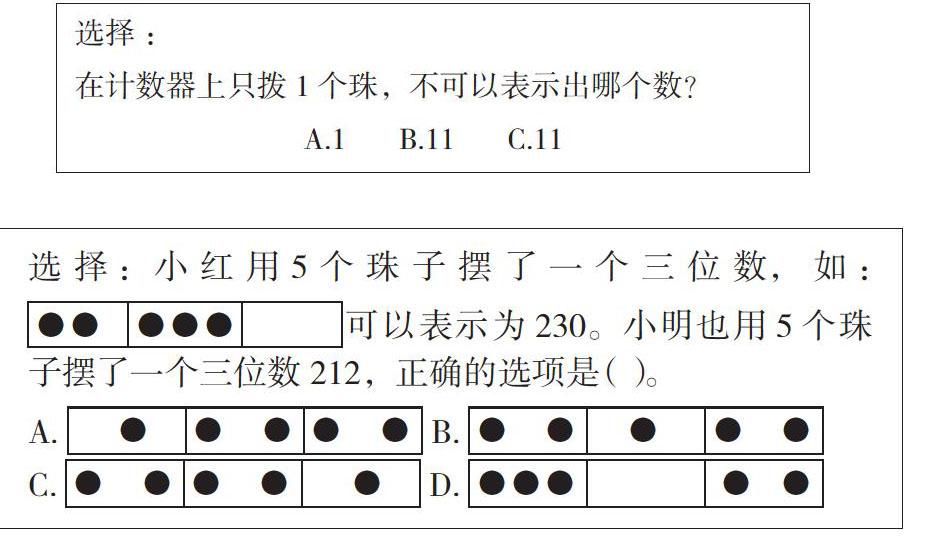
再如，学生认识了千以内的数，为了帮助学生理解各数位上数代表的意义，可以给学生进行下图的变式练习。

题中，在个位、十位、百位上摆5个珠子，摆法不同，得到的三位数不同。正确的选项应是B。此题也有一一对应方法的训练。

西方有一句谚语：“教育的本质，不是把篮子装满，而是把灯点亮。”充分利用直观材料，借助多种模型，充分进行变式训练，学生就会建立起清晰的数的概念，理解数的意义。

参考文献：

王杨灵.凸显本质，优化练习，提升效率——“几分之一”的研究和改进历程[J].小学数学教师， 2015，（S1）.