同一未知数表示多个未知量的方法在数学解题上的应用

罗运友

摘 要：同一未知数表示多个未知量的方法在解决矩形、一次函数和二次函数等问题中有广泛的应用，能够降低学生解题的思维难度，化解由多个未知量带来的解题障碍，充分提高学生解题能力。

关键词： 同一个未知数；矩形；一次函数；二次函数

中图分类号：G633.6 文献标识码： A 文章编号：1992-7711（2016）10-037-01

初级中学学生学习数学的过程中，常常会遇到一个问题当中有多个相关联的未知量的问题，因为未知量较多，学生解决这类问题时感觉茫然、棘手、紧张、无从下手，增加了解题的思维难度和畏难情绪。我们得教会学生掌握和应用“同一未知数表示多个未知量的方法”进行解题，以帮助学生克服和解决这类问题。

先用例题解释“同一未知数表示多个未知量的方法”的含义。例如：用一根长为24㎝的铁丝围城一个斜边长是10㎝的直角三角形，则两直角边长分别是多少？设其中一直角边长为X㎝，，则另一条直角边长度为 （24—10—X） =（14—X）㎝。这样，直角三角形的三边，都用数量表示出来了。再用直角三角形的勾股定理建立方程，即为X+（14—X）=10，解这个方程，就可求得两直角边长，问题得到解决。这里应用到同一未知数X及其代数式14—X表示两直角边的长，用的是同一个未知数表示两个或两个以上未知量的方法，再加上方程思想，问题就得到圆满的解答。

同一未知数表示多个未知量的方法在数学解题上有广泛的应用。

一、在矩形中的应用

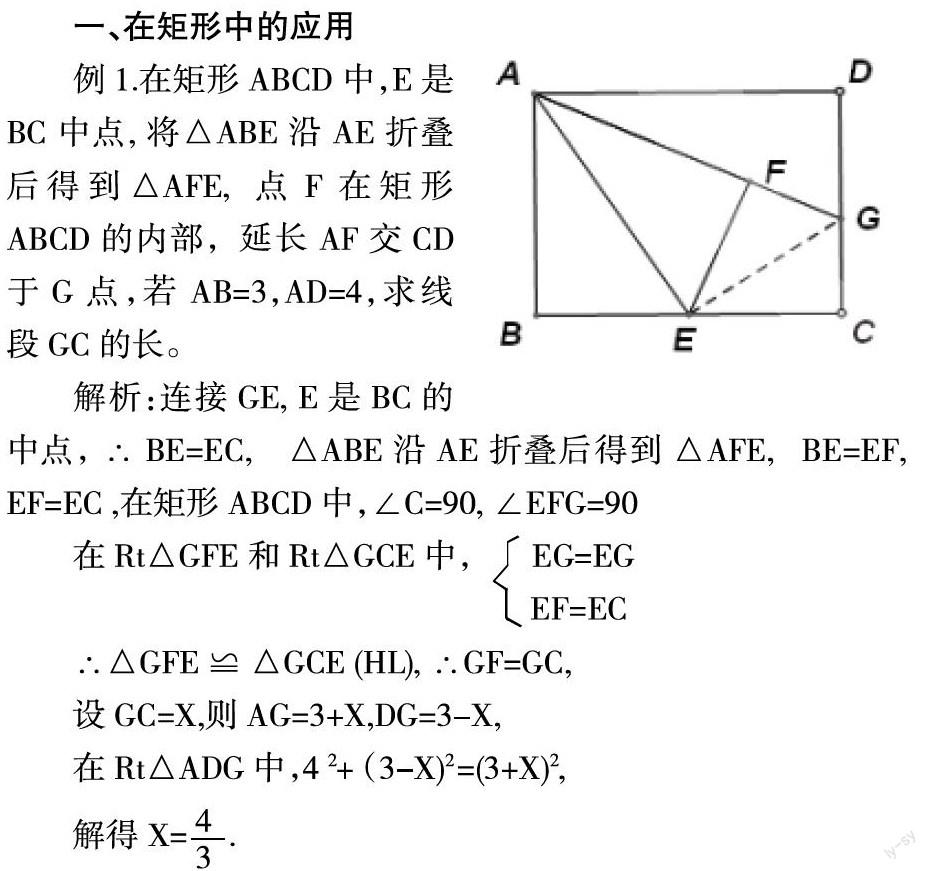
例1.在矩形ABCD中，E是BC中点， 将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD的内部，延长AF交CD于G点，若AB=3，AD=4，求线段GC的长。

这里应用X及其代数式表示了GC、AG和DG这三个未知量的长度，为学生进一步应用勾股定理，建立方程，求出GC的长度，有效扫除了未知量较多而导致思维障碍上的难度，为学生增强了解题的自信心。

二、在一次函数中的应用

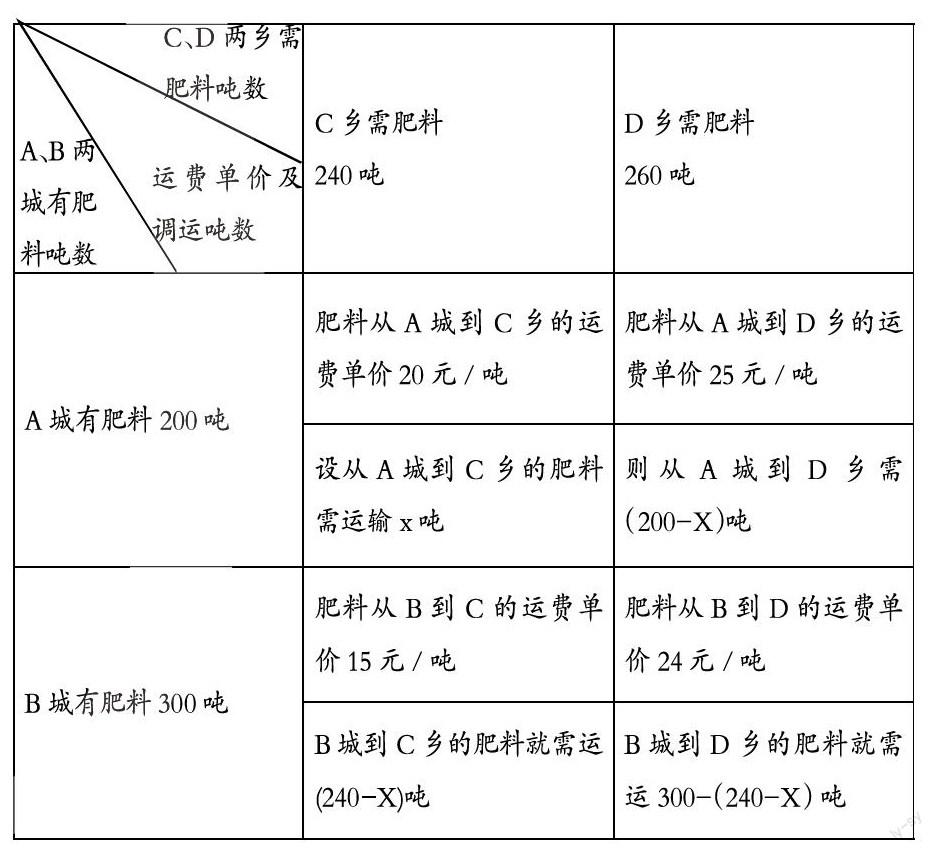
例2.A城有肥料200吨，B城有肥料300吨，现要把这些肥料全部运往C、D两乡，从A城运往C、D两乡的运费单价分别为20元/吨和25元/吨，从B城运往C、D两乡的运费单价15元/吨和24元/吨。现在C乡需要肥料240吨，D乡需要肥料260吨，怎样调运肥料，可使总运费最少？

解析：本题已知和未知的数量都较多，学生解题的难度较大，引导学生画出如下关系图形，用同一未知数x及其代数式把全部未知量都表示出来，就会清晰、明了，该如何求解。图表如下。

题中的未知量有A城运往C、D两乡的肥料各多少吨，B城运往C、D两乡的又各是多少吨，然后才能计算总运费。若设A城运往C乡的肥料有X吨，则可用X的代数式表示A城到D乡， B城到C乡， B城到D乡的肥料分别为（200—X）吨、 （240—X）吨、（60+X）吨 ，又因为X表示从A城运往C乡的肥料吨数，所以X的取值范围是0 ≤ X ≤ 200，总的运费表示为20X+25（200—X）+15（240-X）+24[300—（240—X）].

设总的费用为y， 则有y=20X+25（200—X）+15（240-X）+24（60+X），（0 ≤X≤ 200）。化简得y=4X+10040，（0≤X≤200），

这就变成了一次函数，由一次函数知识可以知道，当取X=0时，总的运费就最少为y=10040（元）。本题应用了一个未知数及其代数式把多个未知的数量表示出来，再利用一次函数上的知识，轻松顺利完成了此题的解答。