功能关系中系统选择对简化力学问题重要性分析

陈志瑶 令维军

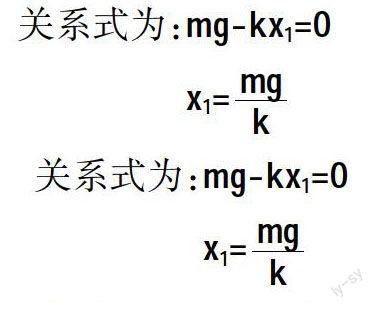
摘要：利用功能关系分析物理运动与相互作用规律是高中物理解决力学问题的常用方法，其中功能关系中系统选择是解决问题的关键。本论文通过分析力学问题中的不同系统的选择，指出正确的选择系统，可以简化问题，更加深入物理本质，突出物理意义，对解决力学问题具有重要的意义。

关键词：功能关系；系统选择；机械能；保守力做功

中图分类号：G642.0 文献标志码：A 文章编号：1674-9324（2016）17-0117-03

在人教版普通课程标准实验教科书必修2（2010年4月第三版）第七章中开始做功和能量问题的教学，纵观教材可以发现，教材对能量问题的基本线——功能关系分析不够明确，容易给初学者混乱的感觉，而功能关系是分析物体的运动与相互作用的最基本规律，也是研究物理力学问题最基本的常用方法。

一般情况下，运用能量观点分析解决问题的基本思路，运用功能关系解决力学问题步骤的第一步就是对于研究系统的正确选定，对于高一学生的认知水平来说，要运用功能关系分析解决问题，首先要做的就是确定研究对象（即系统），这是涉及功能关系中问题分析的关键所在。要顺利解决问题，首先要选择恰當的研究系统，明确外界与系统之间的做功情况，通过分析外力，非保守内力和保守内力的做功，从而找出它们之间的内在联系，更好地利用功能关系解决实际力学问题，在处理任何力学问题的过程中能够形成举一反三的解题思路。

一、系统选择在功能关系中重要性的理论阐释

在力学中，提到系统选择我们就自然而然地想到功能关系，功能关系与能量密不可分，能量、功能关系、系统选择之间的关系是怎样的呢？系统选择在功能关系中问什么这么重要呢？下面我们就三者之间的关系及重要性进行阐述。

1.物体具有能量。教材在第七章以能量问题为引子，用伽利略的理想实验引入思考，“某个量是守恒的”，这个量就叫能量。可以看出能量概念是物理中的一个比较抽象的概念，在物理学的发展过程中，能量的概念几乎是与人类对能量守恒的认识同步发展起来的，能量的概念之所以重要，就是因为它是个守恒量。我们知道从能量观点分析和解决问题，需要有较高的思维起点，需要学生具有综合运用所学知识，以及对物理过程进行全面、深入分析的能力，在高中物理教学中，指导学生学好这部分内容，使学生真正全面正确理解及熟练运用能量知识解决物理问题显得很重要，而我们的能量又跟力学紧密联系着，并且是引出功能关系的源头，所以重要性就不言而喻了。

2.功能关系很重要。能量是引子，功能关系就是主干了。所谓功能关系即物体做功和能量转化之间的关系，就是外力做的功与物体能量变化之间的关系。这在整个中学物理教学中有着十分重要的地位，也是高考必考点之一，它贯穿于力学、热学、电磁学、光学和原子物理学各个部分。我们知道力学中的功能关系分析是第七章教材能量问题的基本线，是主干，是引导，运用功能关系的第一步系统选择来解决力学问题成为解决该问题的关键所在。教材以动能定理引入功能关系（动能定理：力在一个过程中对物体做的功，等于物体在这个过程中动能的变化）[1]，动能定理的研究对象只能是单个物体，如果研究的不仅仅是单个物体而是系统，对功能原理加深理解就是外力和非保守力所做功之和等于机械能的增量[2]，可表示为ΣW外+ΣW非保内=（Ek2+Ep2）-（Ek1+Ep1）=Δ（Ek+Ep）=ΔE。如果外力和非保守力做功为零，此系统机械能守恒。

在解决力学问题上，机械能守恒定律只适用于惯性参考系，且物体的位移、速度必须相对同一惯性参考系。但在解决实际力学问题中，当外力和非保守力做功或其代数和不为零时，机械能守恒的条件是无法严格满足的，这是因为物体运动时总要受到空气阻力和摩擦力等非保守力的作用，并始终做功，因而系统的机械能要改变，但是当摩擦力等非保守力的功同机械能相比可忽略不计时仍可用机械守恒定律来处理问题。在机械运动的范围内，我们所讨论的只是机械能（或动能和势能），可知，只有外力做的功ΣW外和非保守内力做的功ΣW非保内才会引起机械能的改变。机械能守恒定律是功能关系的特例，在这类问题中，系统选择很重要。

3.功能关系系统选择的重要性。我们知道，要解开一团线，找到线头是极为重要的。要功能关系简洁地解一道力学题，第一步最重要。运用功能关系解决力学问题的第一步就是对于研究系统的正确选定，这是功能关系中问题分析的关键所在。要顺利解决问题，首先要选择恰当的研究系统，明确外界与系统之间的做功情况，通过分析外力、非保守内力和保守内力的做功，从而找出它们之间的内在的联系。这样就能快速、正确、简洁地解决你需要解决的问题。

以上分析可以看出，能量、功能关系、系统选择之间的关系环环相扣，缺一不可。正确地选择系统，可以避免很多的不必要的麻烦，尽量选择包含保守力的系统，这样保守力做功可以直接通过势能变化量来表示，使功能关系的表达式物理意义更加清楚明了。同时有利于问题的简化，更加突出物理意义，这对于我们用物理思维解决力学问题有导航的意义和作用。

为了加深对功能原理系统选择的深入理解，我们通过具体实例来说明如何运用功能原理解决力学问题。

二、系统选择在功能关系中的案例解析

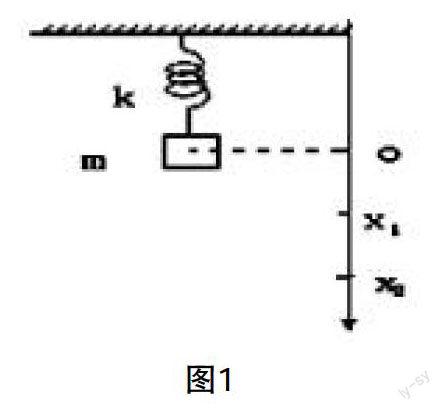
案例1：如图1所示，一个劲度系数为k的弹簧上端固定，下端挂了一质量为m的物体，先用手托住，使弹簧保持原长。设x轴向下为正，取弹簧原长处为坐标点o。

若将物体拖住缓慢放下，到达静止时，弹簧的伸长量x1是多少？

若将物体突然放手，物体到达最低位置时，弹簧的伸长量x2是多少？

分析：研究对象是一个系统，当选择系统的不同，所列出的关系式包含的意义也不同，我们以下列所选的系统举例列出以下列物体为系统时的功能关系式：

1.m，k，地球；2.m，地球。

（1）由于是缓慢放下，物体在整个下落过程中可以近似为是受力平衡的。

①以m，k，地球作为系统。在下落的过程到达o点（平衡位置）时静止，在这个状态下物体（外力）不做功，这时m只受到竖直向下的重力和竖直向上的弹力，它们在这里只扮演内力的角色。

②以m，地球作为系统。静止时，重力是m的内力，因为平衡，弹力在这个系统充当了外力。

小结：以m，k，地球作为系统时，在静止状态下物体（外力）不做功，这时m只受到竖直向下的重力和竖直向上的弹力，要给高一的学生区分外力在这个时候是一个内力的角色是不容易的，他们的物理知识容量还没有达到那个层次，很容易和之前的知识点产生混乱。

在选择以m，地球作为系统的过程中，重力主要是地球吸引力的作用下所产生的，在这个系统中的重力是一个内力，高中一年级的学生已经学过重力是保守内力知识点，不用过多的解释，不容易造成混乱，因此，在这个系统中理解这个案例的问题以及解题思路和所列出的关系式比较容易让读者（学者）接受。

（2）设弹簧原长处于重力势能和弹性势能的零点，且此时物体静止，因此，该状态系统机械能为零。

①以m，k，地球作为系统。突然放手，这时系统机械能守恒，系统在m下落的过程中弹力这个外力做功和非保守内力重力做功都为零，机械能为零，以o处为零势能点，根据机械能守恒，最低位置静止状态，动能为零，两状态机械能相等。

当以m，k，地球作为系统。突然放手，动能和势能相互转化，在物体运动的过程中系统机械能守恒，机械能为零，静止状态，动能为零，两位置点机械能守恒。在这个系统中很容易理清运动关系得出精确的关系式。而以m，地球作为系统静止时，左边，弹力就要充当外力的角色，并且外力做了功，等于右边动能的变化，而右边是静止，动能为零，重力为保守力，机械能的增量，关系式可以列出来，但这个关系式用物理理论是不可以相等的，是说不通的。因此，合理地选择系统很重要。

案例2：如图2所示，在水平桌面上放在质量为M的木块，M的一端与劲度系数为k的轻弹簧相连，并固定在墙上，另一端经轻滑轮与下垂的重物质量为m的C相连，设M与桌间摩擦系数为μ，其余为光滑接触，开始时M静止于平衡位置，求当m下降距离为d的速率为ν有多大？[2]

分析：这个题目整个系统包含了重力、弹力、摩擦力做的功及机械能的变化，我们以下列所选的系统举例列出以下列物体为系统时的功能关系式：

1.M，m；2.M，m，k，地球；3.M，m，k；4.M，m，地球。

根据功能原理和题目所要求的四类系统，可分别得出如下关系式：

①以M和m作为系统，在整个运动过程中，内力和外力的确定与所选取的系统有关，显然在这个系统中重力、弹性力均为外力，摩擦力做的功可视为系统的外力负功，可得到外力做功之和等于机械能的增量。

②当以M、m、k和地球作为系统时，我们发现这时候的重力和弹性力以内力的角色出现，外力就只有摩擦力，可得到摩擦力做的功就等于整个机械能的增量减去内力做的功。

③当M、m、k作为系统时，这时系统外的重力和摩擦力显然是外力，我们知道外力做的功等于机械能的增量减内力做的功，由题目可知弹性内力做的功是负功。

④当M，m，地球为参考系，也就是把重力就作為内力，这个时候弹性力，摩擦力做的功就是外力做功。

在这里我们需要注意的是，系统内保守力做的功的量值与其相应的势能增量是相同的，在功能关系中决不可重复计入。如④式中，重力作为内力角色其势能变化已在等式右方考虑，等式左方就不得计入，并且弹性力作为外力做功已在等式左方考虑，等式右方就不得重复入内。

从以上分析中，将M，m，k，地球看作一个系统物理意义更加明显，系统中重力和弹力变为内力，由于它们为保守力，其做功可以通过重力势能和弹性势能的改变来表征，系统只有摩擦力为外力，其做的功可以表达为整个系统机械能的增量。使表达表达更加清楚明了，避免了重力和弹力做功的重复计入的混乱。

三、小结

在人教版普通课程标准实验教科书必修2（2010年4月第三版）中可知机械能守恒定律只适用于惯性参考系，如果系统选择不同，在一个系统适用的机械能守恒定律在另一个系统中则不一定机械能守恒，通过以上案例，我们可以看出，以不同的系统为参考系，则作用力的性质是不同的，在一个系统中的内力在另一个系统中可能为外力，表达式中这个力作用的涵义就不同。教师在讲解力学中功能关系问题（适用于高中一年级学生）时，在系统完全确定后，等式左面部分代表外力和非保守力做的功，右面为机械能的增量。因此系统的选择直接影响功能关系的表达式，我们在选择系统时，尽量选择包含保守力的系统，这样保守力做功可以直接通过势能变化量来表示，使功能关系的表达式物理意义更加清楚明了。同时有利于问题的简化，更加突出物理意义。

系统的选择，对应了不同的功能关系，深刻理解系统选择，对很好地理解功能关系以及发散思维是很有优势的，因此在解题过程中教师可以适当扩展，指出系统选择的重要性。

参考文献：

[1]普通高中课程标准实验教科书·物理（必修2）[M].北京：人民教育出版社，2010：101.

[2]王少杰，顾牡.新编基础物理学[M].北京：科学出版社，2012，（6）：37-53.

[3]陈震.功能关系及常用的八种表达式[J].理科考试研究综合版，2013-09-1：50.

[4]余俊文.浅析去”功能关系”后的两个瑕疵[J].教学与理论，2013-11-1：82-83.

[5]朱伟华.能量教学的基本线——功能关系（对人教版高中物理教材处理功能关系的探讨）[J].实验教学研究 实验教学与仪器，2010，（6）：75.