格子Boltzmann方法在GPU平台下对多孔介质流动的模拟

摘 要：GPU有着强大的并行计算能力，现在越来越多的被人应用到科学计算领域了。格子Boltzmann是一种模拟不可压缩流动的计算方法，由于其具有天然的并行性，因此本文利用GPU的并行计算能力，在GPU平台上，利用格子Boltzmann模拟周期性的绕方块多孔介质流动，在保证程序结果的计算精度的情况下，极大的提高了程序计算效率。同时将计算结果同有限元的结果进行比较，也得到了较好的计算结果。

关键词：GPU；格子Boltzmann；多孔介质；并行计算

在近20年来，格子Boltzmann方法在计算流体流动的模拟中，起到了很大的作用。但是，与此同时，格子Boltzmann（LBM）方法，在计算过程中，有着计算量大，计算时间长，内存消耗大的特点。但是由于LBM方法是一种显示计算格式，在计算的过程中，只需要利用邻近网格点的信息，因此该方法有着良好的并行性，尤其是在GPU平台上，可以达到很高的并行效率。

GPU 是一个大规模并行计算架构，被广泛的用于图像和非图像计算领域，机器学习，图像，语音等领域都有着应用。GPU的主要优势在于单位时间的浮点计算能力远远的高于CPU的浮点计算能力[ 1 ]。

对于多孔介质流动的数值模拟，大多数情况下，多孔介质流动，都属于缓慢流动，而在模拟缓慢流动的数值方法中，LBM方法是其中一种相当广泛的方法。关于LBM对于多孔介质的流动，在很多领域中都有着重要的应用：复合材料、流变学、地质学、统计物理、生物科学等诸多领域都有着广泛的應用。

在本文中，我们实现了一个通用的LBM在GPU上运行的程序，为了减少数据从CPU内存上到GPU内存上拷贝的消耗，我们将LBM算法中的每一步计算都放在GPU上面来实现。

本文的程序是基于nVIDIA公司CUDA C 语言实现的。一共分为三个部分，第一部分首先介绍了LBM方法，第二部分介绍了LBM方法在GPU平台上的实现。第三部分，我们利用实现的程序对多孔介质流动进行模拟，并进行相关的计算，将计算得到的结果与其他文献结果进行比较，都吻合的很好。

1 格子Boltzmann方法

那么在本文中，该方法由如下几个步骤来实现：

1）对fi进行流动演化；

2）通过fi来计算守恒变量dr和u；

3）利用u*=u+adt/2计算u*，其中a=F/r0，这里F代表外力；

4）利用计算出来的u*和dr计算矩空间的平衡态分布函数mieq；

5）利用fi来计算mi；

6）计算u**=u*+adt/2=u+adt；

7）将mi映射到分布函数空间得到分布函数fi；

8）计算碰撞后的分布函数。

图中的圆点代表每个粒子，从图中可以看出，粒子的分布函数fi只会迁移到周围相邻的几个点。在实际利用格子Boltzmann计算中，需要计算的介观粒子往往很多，并且在模拟多孔介质的流动过程中，往往需要迭代很多的时间步，才能得到稳态流动的数值解。因此一个二维问题的串行程序，往往需要计算几天甚至一个月的时间才能得到计算结果。在GPU上，最基本处理单元是SP（streaming processor），计算过程中，具体的指令和任务都是在SP上进行处理的。GPU进行并行计算，也就是很多个SP同时做处理。

本文程序的编写，采用的是CUDA平台。在CUDA平台上，最基本的处理单元是thread，一个CUDA的并行程序会有多个threads来执行。一定个数的threads会组成一个block，同一个block中的threads可以同步，也可以通过共享内存（shared memory）通信。同时，多个blocks则会再构成grid。

在GPU中，一个GPU所拥有的Thread往往有很多个。在本文所使用的Nvidia-K40的显卡中，采用的计算架构是Tesla Kepler，该架构下面，所能够调用的Thread多达两千万个。

因此，为了提升计算速度，本文在编写多孔介质流动模拟程序的时候，采用的是一个Thread处理一个格子上面的计算。同时，因为计算过程中，需要经常用到格子的离散速度{ci：i=1，2，…，9}，矩阵M，矩阵M的逆矩阵，所以为了优化程序对这些量的访问速度，本文将这些量放入常量内存。

同时，在每一步计算过程中，都会用到矩空间的平衡态函数，为了提高函数的调用效率，本文对于矩空间的平衡态函数采用宏来进行预定义。

由于在计算过程中，会涉及到介观粒子的迁移，所以对于介观粒子的分布函数，只能存放在GPU的全局内存里面（global memory）。但是本文模拟的是多孔介质的流动，该问题的计算区域示意图如下图所示：

如上图中，图（a）为整个多孔介质流动的结构，黑色部分为固体，空白区域为液体。由于多孔介质流动是属于缓慢流动，所以在本文中，可以将问题的计算区域抽象成如图（b）所示的计算区域。边界条件，对于固体边界采用的是无滑移边界条件，对于上下左右的流体边界，采用的是周期性边界条件。

3 数值结果

3.1 数值解的收敛性

从文献[2]可以知道，格子Boltzmann程序的精度是二阶精度，也就是说，多孔介质的程序计算结果是正确的话，那么该程序的收敛阶必须是二阶收敛。

下面给出不同固体体积分数的情况下的收敛阶。在本文中，固体体积分数由如下所示的式子表示：

如下表所示，给出了a=0.9025，0.01这两种情况下的收敛阶。

从上面表可以看出，不管a=0.9025是a=0.01还是的情况下，计算出来的收敛阶都接近2，这也就说明了本文所编写的程序收敛阶为2，所以由此可以看出此多孔介质流动的模拟程序的结果与理论相符合。

3.2 渗透率的计算

同时，由于多孔介质流动多为缓慢流动，对于缓慢流动，存在达西定律，达西定律的公式为如下所示：

其中U为多孔介质流动的平均速度，K为多孔介质的渗透率。

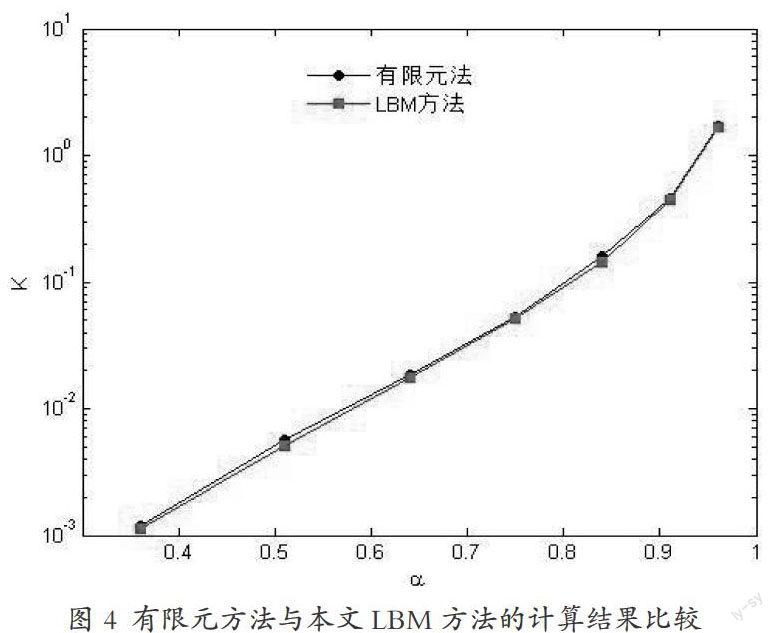
本文将格子Boltzmann方法计算出来的渗透率同文献[3]中的结果进行比较，结果图如下所示：

从上图可以看出，本文所采用的数值方法的GPU程序，与文献[ 3 ]所采用的有限元方法的计算结果吻合的相当的好。

4 结论

从前面的章节可以看出，本文基于GPU平台的多孔介质数值模拟，所得到的结果与理论吻合的很好，与此同时，计算出來的渗透率同有限元计算得到的结果也是一样的，与此同时，本文的程序是基于GPU平台下的大规模并行程序，在模拟同样的问题，同样的网格尺度的情况下，本文所用的时间是普通串行程序的几十倍，并且随着网格的增多，由于GPU里面依然是一个thread处理一个格子，但是串行程序却是一个线程处理所有的格子，相比之下，在迭代相同的步数情况下串行程序所消耗的时间会越来越多，但是本文的GPU平台下的并行程序所消耗的时间却不会有太大的变化。

参考文献：

[1] Nit C， Itu L M， Suciu C. GPU accelerated blood flow computation using the Lattice Boltzmann Method[C].High Performance Extreme Computing Conference （HPEC），2013 IEEE. IEEE，2013：1-6.

[2] He X，Luo L S.Theory of the lattice Boltzmann method：From the Boltzmann equation to the lattice Boltzmann equation[J].Physical Review E，1997，56（6）：6811.

[3] Yazdchi K， Srivastava S，Luding S. Microstructural effects on the permeability of periodic fibrous porous media[J].International Journal of Multiphase Flow，2011，37（8）：956-966.

作者简介：

顾超（1991-），男，汉族，湖北仙桃，硕士，研究方向：计算流体力学。