高中立体几何解题研究

魏胤呈 刘丹

摘 要：高中立体几何主要是对我们高中生的空间想象能力、逻辑思维能力等进行培养，在高考中，立体几何也是考察的重点内容之一，因此高中立体几何的解题有着重要的意义。本文主要从高中生的角度对高中立体几何进行研究和分析，对其中的解题方法和思路进行了探讨，对提高高中生立体几何解题能力有着一定的影响。

关键词：立体几何；解题；研究

在新课标的要求下，高中立体几何的教学有了新的教学目标，在进行高中立体几何的解题过程中，就是对解题方法的不断重复和巩固。个人认为在高中立体几何解题过程中，应该培养的是我们学生的解题能力，我们应该如何去发现问题和解决问题。通过立体几何来分析问题、解决问题，培养自己的空间想象能力和数学思维能力。

一、高中立体几何解题理论基础

对高中立体几何问题进行解决是一个学习的过程，不仅仅是对以往所学的知识的运用，同时也是一个全新的学习过程，在这个过程中，我们不断的进行假设、验证，最终得到正确的答案。数学思想方法基础在立体几何的教学中也是至关重要的，在解决一个立体几何问题的过程中，数学思想被反复的应用。可以说数学思想是一个问题的灵魂，运用的数学方法是数学思想的具体体现。具体而言，数学思想有函数思想、转化思想、方程思想、数形结合思想、分类思想和归纳类比思想等。种种不同的数学思想为高中立体几何问题的解决奠定了良好的理论基础。我们只有不断的对各种数学思想进行熟练的运用才能不断的提高自身的立体几何解决问题的能力。

二、从学生的角度看高中立体几何学习

1.学习手段单一，影响学习效果

现在，高中立体几何的学习方式过于单一，教师不能根据立体几何的特点选择有效的教学手段，黑板和口授是最为主要的学习方式，这样的学习方式是不能满足我们高中生对于立体几何空间想象的要求，也不能对于教师所描述的物体进行想象和理解，学习效果不明显。久而久之，我们对于高中立体几何的问题感到极为头疼，学习兴趣也是逐渐的丧失。学习手段单一是直接影响学习效果的原因之一，我们无法克服对于空间想象的困难，相关的知识点和概念理解不透彻，导致上课听课效果差。

2.空间想象能力不足

与真实的图形结构相比较，立体几何对于我们的空间想象力的要求比较高，而整体来看，我们的空间想象能力较差，还是不能真正的理解立体几何与真实图形之间的差异，想要将立体几何图形转化为语言更是比较困难。比如，在立体几何中，一些看似不平行的线段，在实际的图形中是平行的，我们对此理解困难，导致很难解决好立体几何问题。还有在立体几何题目中，经常需要去证明一些线段之间是相互垂直的，但是在所给图形中看起来是不垂直的，这样让我们去证明就会产生困惑，这些问题都是因为我们对于立体几何的空间想象能力不足，不能充分的理解问题，从而导致学习困难。

3.立体几何概念的理解能力较差

在立体几何中，一些概念是十分重要的，是为以后深入学习立体几何的保障，然而因为我们高中生的空间想象能力不足，理解概念的能力较差，很多时候都是采用死记硬背的方式，无法对于立体几何的概念彻底理解，导致在解题的过程中碰到种种问题，只能生搬硬套相关的公式，最后往往是无法得到正确的结果。因此，提高我们的立体几何概念理解能力和空间想象能力是解决问题，提高立体几何能力的根本。

三、立体几何解题常用方法分析

1.数形结合法

数形结合法是我们在解决问题中常用的方法之一，将数学问题和几何图像相互转化，将一些抽象的数学语音通过直观的图像来表达，这样能更加容易理解，化抽象为具体，将一些复杂的立体几何问题简单化。数形结合法的基本思路是根据题目中数的结构特征，构造相应的立体几何，在利用图形之间的特点和规律来解决问题，或者是将一些复杂的图像利用代数的形式表达出来，更加容易的解决问题。

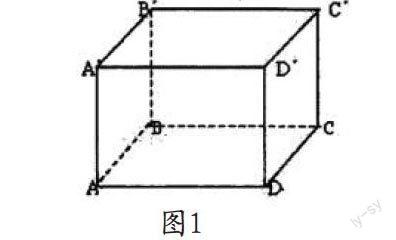
具体案例，如图1所示：在一个3m×4m×5m的房间中，一只蚂蚁想要从长方体的顶点A爬行到顶点C?，计算蚂蚁爬行的最短距离。

面对此类问题，我们首先应该想到的是这个问题是一个最短距离的问题，因此，将空间立体几何转化为平面时是解决问题的最简单有效的方式，数形结合法在此过程中就能得到充分的利用。

2.向量法

在新课标立体几何解题教学中，向量法也是我们解决立体几何问题的重要方法之一。利用三视图和斜二测图，经过数学语言的表达，最后使用向量法进行处理，可以大大降低立体几何的难度。在运用向量法解决问题的过程中，主要是对向量的位置关系和数量关系的应用。

在具体的向量问题中，向量之间的夹角和相关向量之间的垂直、平行关系都可以转化为向量之间坐标的运算，尤其是在求解异面直线间距离问题时，利用法向量，通过向量之间的计算来求解答案。向量法在立体几何的解题中有着重要的地位，很多无法直接求解的问题都可以利用向量法来解决，在一些选择填空中利用向量法不仅可以节省时间，同时还能大大提高答案的正确率。

3.割补法

通过对几何图形的分割或补充来简化问题的方式就是割补法，这种解题方法蕴含着一种构造的数学思想，也是对立统一辩证思想的具体表现。割补法中的补形法是将原来的几何图像补充为一个新的几何体，便于观察和解题。而分割法则是将原来的几何体分割为多个我们所熟悉的几何体，这样能够更加便于问题的解决。在高中立体几何中，利用割补法来进行解决实际问题，对于我们的立体思维的培养和拓展有着一定的意义。

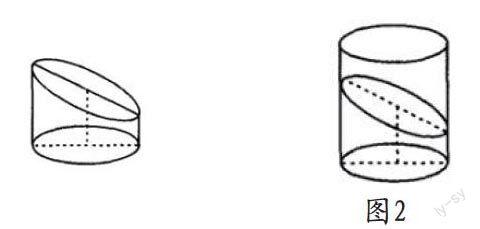
具体案例：如图2所示，一个被平面所截的圆柱体，在被截之后，侧面最长母线为5，最短母线为2，底面半径为3，求该几何体的体积。

对于这样的问题，我们可以运用割补法将两个相同的几何体想拼接，作为一个完整的圆柱体，这样就能利用圆柱体的体积公式来简单的解决问题。将问题简单化就是利用割补法的意义所在。

四、立体几何解题的建议

1.利用多媒体教学，提高学习效率

我们高中生的空间想象能力和逻辑分析能力还是有一定的缺陷，因此在观察事物或解题的过程中会喜欢比较直观的方法。往往立体几何中复杂的逻辑分析和抽象的图像会让我们望而祛步，枯燥而无趣的学习过程也会使我们学习兴趣不高。因此，利用多媒体教学能够充分的解决抽象和逻辑分析复杂的问题，在多媒体教学中，通过动画演示能够将立体几何的演变生动、直观的展示在我们的面前。在多媒体设备上，立体几何与实物相结合，对几何体的特征进行分析，总结其特点，这样视听结合的方式能够大大提高我们的学习效率。在立体几何概念、定理和公式方面，应该利用多媒体资源和信息，将难以理解的概念和定理、公式等进行演示，帮助我们来充分理解，从而提高立体几何解题效率。

2.立体作图，培养学生的空间思维

我们在初中所学的平面知识对学习立体几何有着一定的阻碍，思维还停留在平面思维中，没有空间想象的思维，在遇到空间几何图形时首先想到的就是平面图形，因此，在平时的做题和训练中，就应该培养我们进行立体作图，对其空间思维进行培养，让我们逐渐的适应空间中的异面直线和图形旋转等问题。首先，教师应该带领我们进行一些简单立体图像的学习，在纸上将自己所看到的立体图形画出来，这样由简单到复杂，逐渐的培养空间立体思维。其次，教师应该逐渐的培养我们的识图能力，在实际题目中，根据所提示的信息，将需要的图形画出来，以便于解题。

3.加强我们的理解与应用能力

对于立体几何的概念、定理和公式的充分理解是进行熟练应用的基础，教师需要带领我们弄清楚各个概念、定理和公式之间的关系，将所学的知识形成一个系统的知识网络，在实际做题的过程中，我们可以利用形成的知识网络进行熟练运用。在解题过程中，有意识的培养我们的分析问题和解决问题的能力，灵活的运用公式，同时在做题的过程中对概念、定理和公式作进一步的加深理解。

五、结束语

对于高中立体几何的解题个人认为是高中数学学习中的重点和难点，在现代化信息技术如此发达的今天，教师应该充分的利用多媒体设备来帮助提高立体几何的学习效率，培养我们高中生对于立体几何的学习兴趣，让我们进行主动的学习，帮助我们灵活运用知识点，培养空间想象能力和逻辑思维能力。

参考文献：

[1]底军艳.新课标下立体几何教学的分析与探讨[J].中国科教创新导刊，2014（06）.

[2]王晓峰.高中立体几何解题教学研究[D].内蒙古师范大学，2013.

（作者单位：成都外国语学校）