问题解决教学需要关注什么

张川

随着基础教育课程改革的深入推进，广大教师越来越清楚地意识到：解决问题教学如果只是侧重于具体的解决思路分析，或是增加解决方法的初步感悟与评析环节，是远远不够的。而应当关注隐藏在具体思路和方法后面更为本质也更为有价值的东西，即解决问题策略的教学。课程改革的大量实践证明：如何使解决问题的策略思想转化为学生具体的解决问题能力与行为，是当前迫切需要研究的问题。学生在解决问题的过程中常常出现这样一些现象：不明确问题解决目标，无法正确确定问题解决策略；解决策略选择不当，过程繁难等。笔者认为，要培养和发展学生的问题解决能力，应关注学生问题解决策略的适用性；分析手段的直观性；知识应用的灵活性。

一、问题解决策略的适用性

面对一个题目，如何达成题目的要求，是一切策略的核心，“我们必须对我们所要达到的目的一清二楚”。有了核心，就能有的放矢地在定向分析中探索和研究处理问题的策略，否则，只能是无头苍蝇似的瞎碰。

例如，一位教师在执教《包装中的学问》（北师大版小学数学五年级下册）一课时，学生已经解决了二盒磁带的包装纸大小问题。在此基础上，教师出示四盒磁带，让学生思考“怎样包装最节省包装纸？”

大多数学生不假思索地回答并认为：先动手摆一摆，看有几种包装方式；再分别计算包装纸的面积；最后进行比较。于是，教师让学生在小组合作中加以解决。顺理成章地，小组合作和全班交流的环节让少数学生体验到了巨大的成功：他们展示了自己是如何对包装方式进行分组、比较、筛选、再比较，甚至不用计算就知道最节省包装纸的是哪种方式。只是，如何能让大多数学生都能体验到成功的乐趣呢？

课后，我们对这一问题进行了反思。问题的关键在于：绝大多数学生没有明确解决此问题的目的不是“求多少”，而是“比多少”，由于受到前面学习环节的影响，思维策略拘泥于“一一列举”的不在少数。为此，我们可以适时地引导性提问——这么多种包装方式，我们能否少一些计算？启发学生明确解题的目的在于“比多”，引导学生的思维集中关注“比”，在“如何比”方面想办法。以上案例说明，学生在审题方面，存在个体差异，每个学生都存在一个从幼稚走向成熟、从肤浅走向深刻的过程。学生在选择解决问题的策略时，往往不对路子或是繁难不堪。出现这样的情况实属正常，作为教师，有必要提示学生反思自己的解题策略，对其适用性进行审视和评估，优化或重新选择，采用既能达成题目要求，又富有效率的策略和方式。长此培养下去，学生在解决问题过程的自主性将有望大为增强。

二、问题分析手段的直观性

生活实际问题在情境的呈现、叙述上往往具有生活化、信息分散，存在多余條件等特点。对于学生而言，知识的内在联系比较隐蔽，解决问题的思路不易把握。同时，从小学生的年龄和心理特点考虑，有必要引导学生学会对扑朔迷离的表象进行由表及里、去伪存真的加工改造。达到既能概括出具有本质特征的、规律性的认识，又能易于他们接受与认同，才能在此基础上自主选择有效的解题策略或思路。

据此，笔者认为：在解决问题的教学中，可以适当地鼓励学生运用举例、画图、列表等方式分析问题，在相对直观的条件下进行思维、交流想法、深化认识。

线段图是小学阶段运用非常广泛的一种分析问题的手段。它不仅可以形象、直观地反映题目中的数量关系，启发学生的解题思路，还可以通过画线段图的训练，提升学生思维的敏捷性，提高分析、解决问题的能力。

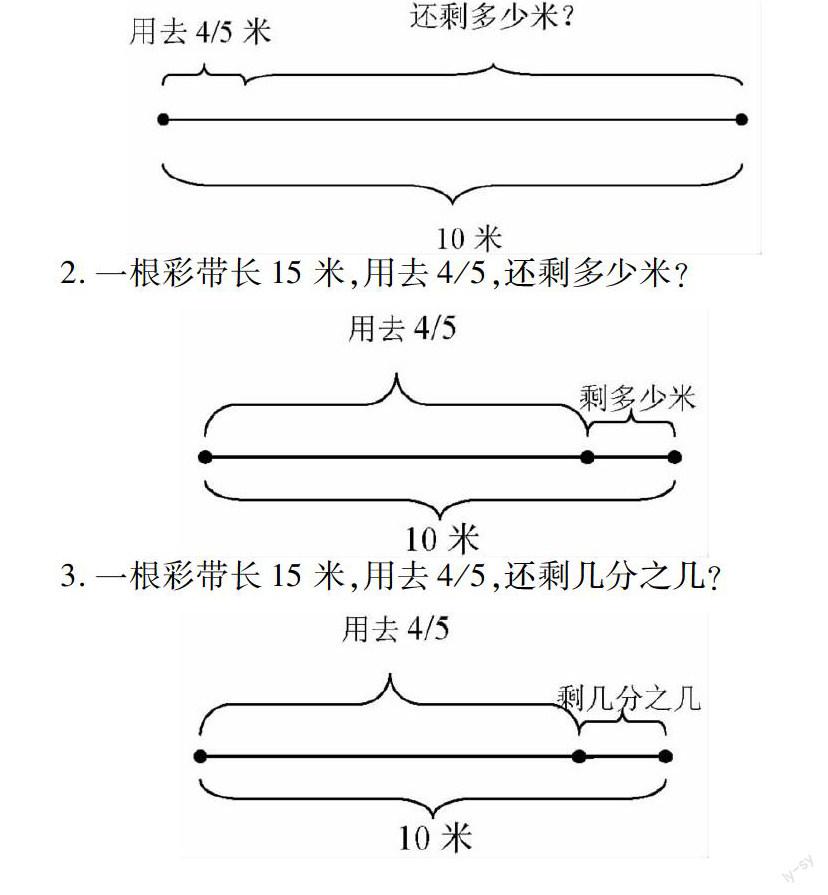
例如，1.一根彩带长15米，用去4/5米还剩多少米？

2.一根彩带长15米，用去4/5，还剩多少米？

3.一根彩带长15米，用去4/5，还剩几分之几？

借助线段图不仅可以帮助学生理解题意、算理和解题思路，而且，如果把相似、相近的题目放到一块，从线段图上进行比较，就能明显地区分它们的异同。从而能减少作业中常出现的错误，提高正确率。

三、知识应用的灵活性

探求解题途径时，学生必须戴上广角镜，多方向、多角度地在题目所涉及的范围内思考。只有视野开阔，才能保证选择、认定解题策略的灵活性和合理性。

在北师大小学数学教材第十册的《购物策略》一课的教学过程中，曾出现这样的情景：教师让学生思考“当所购饮料的总价低于30元时，甲、乙两个超市谁更划算？”，于是，绝大多数的学生立即埋头举例演算起来。只有一位同学没有急于行动，他不慌不忙、若有所思地本子上写了一些数字，草草算了一下，这些都被教师看在了眼里。在全班汇报时，教师最后请他来介绍，这位同学说道：“甲超市‘买大送小，花10元可以买回12元钱的商品，也就是说这个超市实际是打8.3折；而乙超市‘一律九折。所以我认为甲超市更加划算。”话音刚落，教室里已是议论纷纷。……最终，通过全班交流，全体同学不仅达成了共识，而且纷纷赞扬这位同学独辟蹊径，运用折扣的知识解决实际问题。

学生在问题解决中知识综合应用的灵活性表现不是一朝一夕练就的。教师除了利用好教材内容之外，还要善于选择或设计好的问题，让学生习惯于独立思考，逐渐在独立思考的过程中发展其问题解决的灵活性。例如，一位教师在教学完圆柱的表面积之后，出了一道思考题：下图是一块长方形铁皮，利用图中的阴影部分，刚好能做成一个油桶，求油桶的容积（铁皮厚度不计）。