注重过程教学 提高数学能力

秦德宝

初中数学教学的目标是提高学生基础知识、基本技能、数学思维能力、问题解决能力等综合数学能力。课堂教学是培养学生数学能力，提高学生数学能力的主阵地。在教学活动中，要关注学生学习过程，在学生理解、掌握、应用知识与技能的过程中，培养学生的数学思维能力、解决问题的能力，掌握数学思想方法，形成学生继续学习新知的能力。因此，重视过程教学，充分暴露学生的认知发展变化的过程，教师加以科学引领，从而促进学生自主建构知识，这是提高课堂教学效率的关键。

一、经历认知发展变化的过程，提高思维能力

案例：探究等腰梯形性质定理的过程

师：你能用老师给你的矩形纸片剪一刀使它成为一个等腰梯形吗？并说出你在剪的等腰梯形的过程有什么发现？

学生在拿起纸来动手探究后，一位学生兴奋的说：老师，我将纸片对折后，剪一刀就剪出来了。他边说边演示，其他同学观察演示过程。

生2：我发现等腰梯形是轴对称图形，同一底上的两个角相等。

生3：两条对角线相等。

操作是思维的起点，也是认知的来源，实践出真知。学生动手操作，让学生从亲历到感知，从感性到理性，从而发现了等腰梯形的轴对称性、同一底上的两个角相等、两条对角线相等。经历知识发生、发展的过程，在实践中丰富了数学活动经验，培养观察、归纳、概括、类比、猜想的数学思维能力。

师：如何证明你们猜想？

生1：要证两个角相等有几种常规思路：（1）当两个角在同一个三角形时，只需用等边对等角。（2）当两个角在不同一个三角形里时，用三角形全等。所以我想连接AC，BD证明△ABC≌△DCB，从而证明。

生2：我已想过这里只有两条线段AB=DC，BC=CB，不能证明两个三角形全等。

师：如何通过添辅助线构造三角形全等呢？

生3：作AE⊥BC，DF⊥BC，垂足为E、F，图（1）。

师：大家说的都很好，以上这种方法是我们研究问题的一种思路，都需要通过添辅助线，将梯形问题转化为我们已学的知识，在梯形的问题里，我们通常通过添辅助线解决，以上这种转化方法称：作高线。

生4：延长BA，CD交于点E，利用等边对等角。

生5：这里EA、EC不知是否相等，所以不能证明EB=EC，这种方法不行。

生6：过点D作DE∥AB交BC于点E ，得到平行四边形与三角形，图（2）。

师：太好了，这种转化方法我们称：平移一腰，将梯形转化成平行四边形和一个等腰三角形。学习性质定理后，教师及时让学生小结解决梯形问题的常用辅助线作法，体会转化思想。

学生的认知过程是一个对思维不断地进行自我调整、整合的过程，若教师呈现给学生的是优化的思维方式和完美的解题过程，则难以体现出教学思维的真实过程，使得学生只会模仿，不会创新，学生回答问题时只能沿着教师的思路回答，掩盖了学生思维活动的真实过程。在教学中如果充分利用生成资源，沿着学生的思路解下去后展开讨论，肯定同学们的想法，我们发现了一种新的解法。重视过程教学，可以培养学生学习数学的兴趣，提高学生的数学能力，培养学生勇于探索的精神。充分暴露学生的思维过程，使学生体会“数学是思维活动的过程”，从而提高学生的数学思维能力。

二、关注知识与方法的迁移过程，提高数学能力

只重视知识的传授，单纯依靠大量练习达到知识技能的熟练的传统教学只是培养“高分低能”，不会培养出具有数学能力创新能力的人才。解决数学问题的实质就是将原有知识、新知识进行联系、比较和运用，从原有知识迁移到新知识的过程，通过迁移，掌握知识和技能并转化为能力。把所要解决的问题与已有知识进行对比联想，找出其中隐含的关系，为解决问题开辟广阔的空间，实现知识及方法的迁移。

案例 探究梯形中位线及性质定理教学过程。

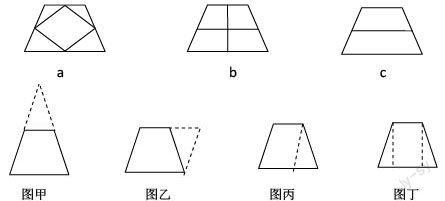
学习梯形中位线概念及探究梯形中位线性质时，学生已经学习了三角形的中位线及其性质，梯形也有中位线，那么怎样探究梯形中位线及性质呢？学生类比三角形中位线，可能画出图a，任意连接两边中点的线段就是中位线，有四条；也有学生画出图b，连接对边中点的线段就是梯形中位线。纠其原因这是旧知对新知产生的负迁移，关键是没有找准新旧知识间的联系结合点，只是通过表象来迁移联想。此时，教师引导学生联系三角形中位线的性质考虑，学生回顾三角形中位线与第三边平行的特性再画出了图c。教师再引导学生类比三角形中位线定义结合图形给出梯形中位线的定义，此时学生很自然的给出了准确的梯形中位线定义。

三、重视数学思想方法的渗透过程，提高数学能力

数学思想方法是数学的精髓，学生只有领会了数学思想方法，才能深化知识的理解，应用知识，形成能力。

案例 探究等腰梯形的判定定理教学过程。

探究：给你矩形、平行四边形、等腰三角形纸片，怎样剪出等腰梯形？通过动手操作学生就会发现：等腰三角形有两底角相等，等腰梯形同一底上的两个底角也相等，他们的性质类似，所以等腰三角形可以得到等腰梯形；有的学生提出，把矩形纸片对折，剪下一个三角形就可以得到一个等腰梯形；把平行四边形剪去一个等腰三角形就是等腰梯形。教师顺势引导学生证明判定定理：同一底上的两个底角相等的梯形是等腰梯形。有了上面的探究，学生的思维活跃开了，很自然想到延长梯形的两腰得到两个等腰三角形（图甲），把梯形补成一个平行四边形去证明（图乙），从“补法”联想到“分法”，添辅助线把梯形分成平行四边形和三角形（图丙），把梯形分成矩形和两个直角三角形（图丁）去证明等。教师及时点拔、归纳，同学们都很好的运用了“转化”的数学思想，通过恰当的添加辅助线，把梯形问题转化为三角形或平行四边形问题得以解决。

学生经历了得到等腰梯形性质的探索过程，发现了等腰梯形与等腰三角形、平行四边形、矩形之间的联系，在探索的过程中，运用了“转化”的方法，得出了梯形问题中添加常用辅助线的规律，形成研究梯形问题的基本技能，领悟了“转化”的数学思想方法，提高了学生的分析问题和解决问题的能力。让学生经历知识的学习和问题的解决过程，在过程里领悟数学思想方法，提高数学能力。

总之，重视数学过程教学，在过程教学中充分暴露学生的思维过程，重视学生迁移能力的培养，加强数学思想方法形成的引导。这样，学生不仅学到了知识，而且学到了方法，提高了能力。

（作者单位：南京市江宁区上峰初级中学）