一种用于波速测试的正演和反演算法

丁健华，宛新林，贺晓华（安徽建筑大学土木工程学院，安徽合肥，230601）



一种用于波速测试的正演和反演算法

丁健华，宛新林，贺晓华
（安徽建筑大学土木工程学院，安徽合肥，230601）

摘要：波速测试的正演和反演算法是通过地表或井间观测到的地震波走时，推算地下或井间的介质速度结构和地震波的传播路径。其步骤如下：（1）数据采集。（2）将地下介质离散成一定大小的网格并初始化慢度（速度的倒数）场，采用射线追踪技术推导各网格节点的射线路径和最小旅行时。（3）建立线性方程组。（4）反演求解线性方程组，并修正初始慢度模型。（5）重复（2）-（4）步骤，不断修正慢度场，直到满足精度要求为止。本文采用最短路径射线追踪正演算法和同时迭代重建（SIRT）反演算法在二维平面上进行求解计算，并且把得到的结果与传统单孔法比较，从而了解本文所采用的波速测试方法的可靠性、实用性及其精度情况。

关键词：最短路径射线追踪；SIRT算法；单孔法

0　引　言

土层波速，特别是剪切波速的研究具有重要意义，因为土层剪切波速关系到场地类别的划分、关系到砂土液化现象和土层的动剪切模量等。目前土层波速测试主要是分为实验室测试和现场原位测试。前者主要应用于场地复杂、无法进行原位测量的重要工程。现场测试波速的方法主要有单孔法、跨孔法和表面波法等。单孔法具有设备简单，操作方便，是应用的较多的原位测试技术，但是单孔法假设地下介质为水平层状结构和地震波沿直线路径传播，这都忽略了地下介质非均匀分布的影响，从而导致计算结果的误差。因此能不能模拟出地震波的真实传播路径，能不能得到地下非均匀介质各点处的波速（即波速场），这就是本文所研究的内容。目前关于这方面的研究很多，也取得了很大进展。其中大部分方法都采用了将地下介质离散成网格并在网格上布置节点，然后，分两步求解：一是正演计算，即计算每个网格节点的最小旅行时和追踪节点的地震波传播路径；二是反演求解，修正模型。在求解过程中需不断地重复这两步，直到前后两次的慢度差满足精度要求为止。网格中的正演求解是通过射线追踪的方法来实现的。

目前，用于射线追踪的算法有很多，如传统的试射法［1］和弯射法［2］、最短路径法、有限差分求解程函方程法［3］、旅行时线性插值法（LTI）［4］等。反演求解线性方程组的方法有最小二乘法（QR）、代数重建法（ART）、同时迭代重建法（SIRT）、分解法（LSQR）［5］等多种算法。各种算法都有各自的优缺点，本文采用的正演算法是最短路径射线追踪算法，它是一种稳定性较好的算法；反演算法采用了SIRT算法，它能够较为准确的反应地下介质的波速分布情况。文中采用了MATLAB编程技术，在二维平面上进行地震波波速的正演和反演计算，得到所有网格节点的波速和地震波传播路径，取接收点所在水平线上的所有节点波速平均值作为该层的波速值，然后，将得到的波速结果与单孔法比较，以确定该方法的可靠性、实用性及其精度。

1　射线追踪

1.1射线追踪方法原理

最短路径射线追踪方法的理论基础是光学中的Fermat原理和图论中的最短路径理论［6］。将地下非均匀介质离散成若干个大小相等的小单元体，并认为这些小单元是均匀的，然后在各单元边界上设置一些离散节点，求解出这些节点处的速度，地下介质的速度模型就可近似的由这些节点速度代替。在网格中，地震波从激发点到接收点一般有很多条路径。每条从激发点到接收点的路径都是由相互连接的节点序列组成的，相邻节点之间的旅行时为节点之间直线距离与两相邻节点的平均慢度之积，整条路径上总的旅行时即为该路径所有相邻节点射线路径旅行时之和。根据Fermat原理，把从激发点到接收点传播时间最短的路径近似为地震波传播路径，该路径即为最短路径射线追踪得到射线路径。

1.2网格模型的建立

网格根据需要可以有多种形状，在二维平面中可以是三角形、平行四边形、矩形等，三维空间中可以采用四面体、立方体单元等。本文研究的是二维平面，在二维网格模型［7］中一般采用矩形网格，将地下介质离散化为m×n个大小相同的矩形网格，地下波速场就可以近似的以这些网格单元的波速表示。在网格边界上，节点的设置存在着多种方法。如可以将节点仅布置在角点上，也可将接节点只规则的布置于角点之间的边界上，当然，还可以在角点与边界上同时布置节点，本文采用将节点仅布置于角节点上的方法。网格上每个节点与周围节点连接方式取决于有效半径r：r=1时，网格节点可以与周围8个节点相连接，r=2时，网格节点可以与周围16个节点相连接，r=3时，网格节点可以与周围16个节点相连接，以此类推，还可以有更多的连接方式，这样的连接方式可以避免在同一方向上射线经过多个网格节点的情况。实际上并非r越大越好，从图1中可以看出，r越大，射线就可能会经过更厚的地下介质，由于地下介质的非均匀性，射线在厚的介质中沿直线传播的可能性很小。所以应根据实际情况选择合适的有效半径，本文采用r=2的连接方式。

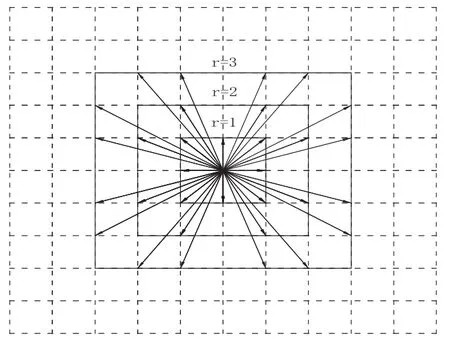
图1　网格模型

1.3最短路径射线追踪的算法

由惠更斯原理［8］可以知道，波阵面上的点可以视为次级波源，向外发射次级波。因此可以将网格上的节点作为次级波源。再由Fermat原理和图论中的Dijkstra算法［9］求出地震波从震源传播到所有网格节点上的最小旅行时［10］。实际上，整个射线追踪过程就是不断向前追踪次级波源的过程。具体步骤如下：

（1）从震源p开始，计算与震源相连的节点A1-A16的旅行时，从中找出旅行时最小的节点A1作为次级波源（如图2所示），并记录A1节点的最小旅行时。

（2）计算与A1相连的所有节点的旅行时（震源P除外），当相连节点为已算过旅行时节点时，需重复计算该节点旅行时，并将算出的最小的旅行时替换为该节点的旅行时，然后在所有已算过旅行时的节点（除震源P和已做过次级波源的节点A1）中找出旅行时最小的节点A13，把A13作为次级波源（如图3所示），并记录A13节点的最小旅行时。

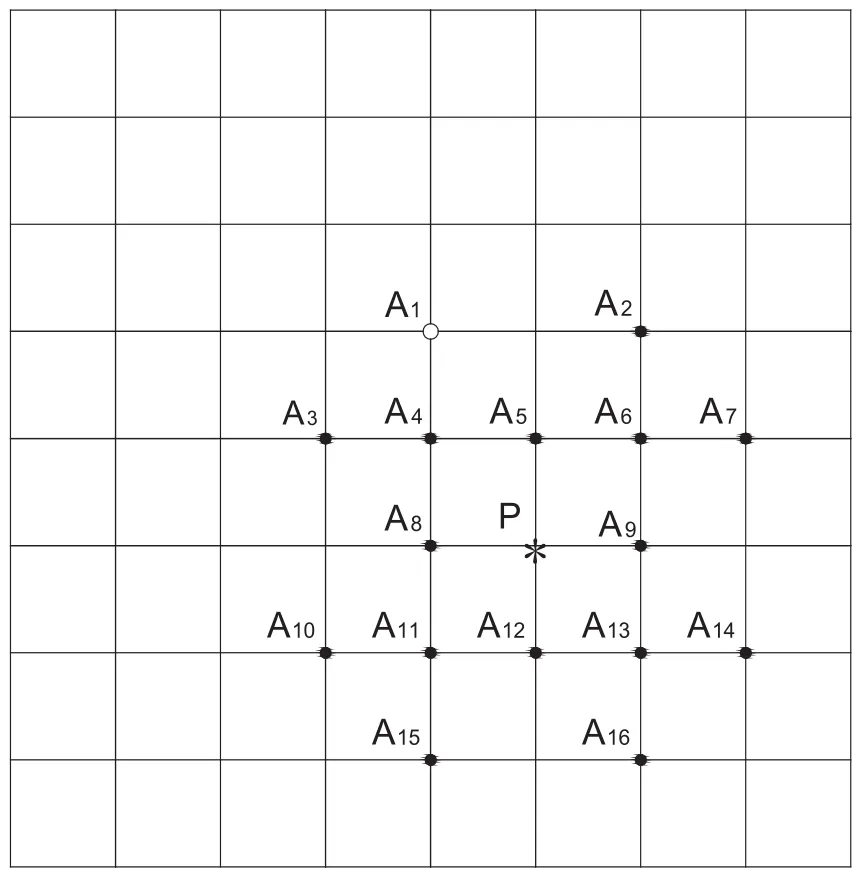
图2　从震源开始追踪次级波源

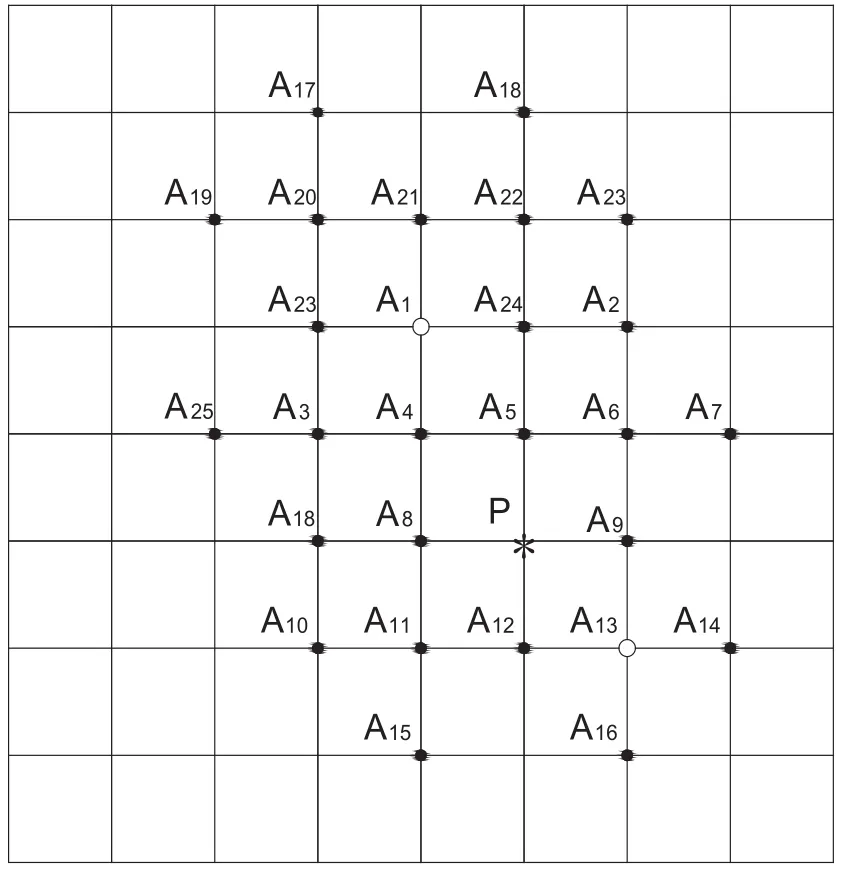
图3　从次级波源继续搜索下一次级波源

（3）重复步骤（2），不断地搜索下一个次级波源，直到网格所有节点都做了次级波源，都计算出最小旅行时为止。在搜索次级波源过程中应同时记录每一次级波源的前一级次级波源。

（4）从接收点开始逆向追踪得到从震源到各接收点的射线路径。

2　生成线性方程组

反演线性方程组是以矩阵形式给出，AS=T，其中A是m行n列的矩阵，其中m为射线路径的条数，即接收点的个数，n等于网格节点总数。A中的i行j列元素有四种可能：若第i条射线路径未通过j节点，则该元素为零；若j节点为第i条射线的起始节点，则该元素为射线路径起始节点到路径第二节点连线长度的一半；若j节点为射线路径起始节点与末端节点之间的点，则此元素为该节点与路径后一节点射线长度和该节点与路径前一节点射线长度和的一半；若j节点为路径末端，则该元素为路径末端节点和前一节点射线长度的一半。S为每个节点慢度构成的n维向量，S（j）为对应于A中第j列节点j的慢度。网格中的节点可以用矩阵索引的方式唯一表示，例如i行第j个元素可以用来表示第i行第j个节点，亦可用一个列向量唯一表示节点，两者之间存在着对应关系，即第i行第j列的节点与向量中的第k个元素对应，k=（i-1）*N+j ，N为节点矩阵的列数。

3　SIRT算法反演方程组

SIRT算法是Simultaneous Iterative Reconstruction Techniques的简称，译为同时迭代重建技术。算法步骤如下：

（2）利用初始慢度值求出每个方程的旅行时估计值：

（i=1，2，…，m。m为射线路径条数。）

（4）计算每个方程对网格中节点的慢度修正值：如第i个方程对第j 个节点的慢度修正值为

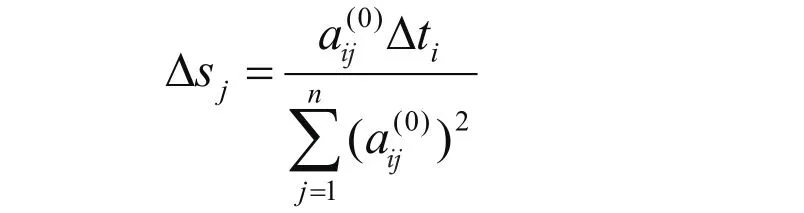
（5）求慢度修正值。将每个方程对节点的慢度修正值求平均，就得到节点的慢度修正值，由于有很多节点没有射线通过，其慢度值便没有得到修正，对于这样的节点可通过插值的方法获得其修正。具体方法是一该节点为中心，通过某一半径r范围内的已修正的节点的慢度修正值对其加以修正：

（其中，di为节点i到所求节点的距离，k为所求节点半径r范围内的已修正节点个数）。

（8）重复上述步骤，直到前后两次的慢度差满足精度要求为止。

4　理论模型与算例

为了验证本文方法具有比传统单孔法更高的计算精度，进行了水平层状理论模型下的波速仿真计算。在此基础上，将本文方法用于工程实例计算，进一步验证本文方法在实际中的可靠性与稳定性。

4.1水平层状模型

模型参数如下：水平方向1.5m，竖向深度10m，模型分为三层：第一层深2m，波速为180m/s；第二层深3m，波速为220m/s；第三层深5m，波速为260m/s。采用单孔法进行原位测试，激发点位于（0，0）处，接收点坐标分别为（1.5，1），（1.5，2），…，（1.5，10）处（模型如图4所示）。分别用单孔法和最短路径射线追踪与SIRT反演算法求得地下介质波速，波速结果如表1所示。

图4　水平层状模型

表1　波速结果

表2　波速和接收点走时

4.2 工程实例

本文以芜湖市某拟建工程为例。该工程总占地面积约2万m²，总建筑面积约为60000m²，其中地下建筑面积约为10000m²。根据现场钻孔和场地情况，选取了现场9号钻孔进行了剪切波试验。该试验将激发点置于离孔边1.5米处，接收点分别位于孔内1m、2m、3m、4m、5m、6m、7m、8m、9m、10m、11m、12m、13m、14m、15m、16m、17m、18m、19m、20m处。分别用传统的单孔法和最短路径射线追踪与SIRT反演算法求得地下介质波速和接收点走时，两种方法得到的结果，如表2所示。

5　结论

（1）由表1数据可知，与传统单孔法相比，本文所采用的方法具有更高的精度。另外，从表2可看出由该方法得到的接收点的走时近似等于现场拾取的走时，由Fermat原理知道该算法得到的射线路径逼近真实的地震波传播路径。

（2）从表中数据可看出最短路径法与SIRT算法结合使用得到的波速与单孔法测试结果总体相差不大，它们都能够得到满足工程精度要求的波速结果。表中数据还表明文中所用算法程序具有稳定性和可靠性。

（3）理论上，网格划分的越细，越能逼近地震波传播的真实路径，得到的结果越精确，但网格划分的越细，节点数越多，计算量越大，从而导致程序运行的时间过长。实际应用中可以根据场地实测资料和工程精度要求来选择合适的网格大小。另外，还可以增加激发点和接收点的数目，使更多的节点有射线通过，以此来提高波速计算的精度。

（4）该方法考虑了地下介质的非均匀性，不仅能够得到地下介质波在地下介质中的传播路径。

参考文献

［1］Julian B R， Gubbins D. Three-dimensional seismic ray tracing［J］. J Geophys， 1977，43：95-114.

［2］Thurber C H， Ellsworth W L. Rapid solution of ray tracing problems in heterogeneous media［J］. Bulletin of the Seismological Society of America， 1980，70（4）：1137-1148.

［3］Vidale J. Finite-difference travel time calculation［J］. Bulletin of the Seismological Society of American， 1988，78：2062-2076.

［4］赵改善，郝守玲，杨尔皓，等. 基于旅行时线性插值的地震射线追踪算法［J］. 石油物探，1998，37（2）：14-24.

［5］Paige C， Saunders M. LSQR： An algorithm for sparse linear equations and sparse least squares［J］. Association of Computational Mechanics Transactions and Mathematical Software. 1982，8：43-71.

［6］李志辉，刘争平. 最短路径法射线追踪的MATLAB实现［J］. 工程地质计算机应用， 2004，36（4）：16-21.

［7］魏亦文. 基于复杂介质最短路径射线追踪层析成像正演研究［D］. 湖南：中南大学. 2007.

［8］陆基孟，王永刚. 地震勘探原理［M］. 北京：中国石油大学出版社. 2011.

［9］张建中，陈世军，余大祥. 最短路径射线追踪方法及其改进［J］. 地球物理学进展， 2003，18（1）：146-150.

［10］喻维秋. 初至波表层模型层析反演及其应用［D］. 成都：成都理工大学. 2007.

A Forward and Inversion Algorithm for Wave Velocity Test

DING Jianhua，WAN Xinlin，HE Xiaohua
（School of Civil engineering ， Anhui Jianzhu University ， Anhui Hefei，230601）

Abstract：Forward and inversion algorithm of wave velocity test to calculate the underground or medium of crosshole velocity structure and seismic wave propagation path through traveling time of the earth's surface or crosshole seismic earthquake wave.The steps are as follows:（1）Data collection.（2）The underground medium must be divided into the same size of the grid and initializes the slowness （the reciprocal of speed），Ray tracing technology is used to derive the ray path and minimum travel time of the grid nodes.（3）Establishing linear equations（4） solving linear equations by using inversion techniques， then correcting the initial model of the slowness.（5）Repeating steps （2） to （4），Continuously revising slowness， until meet the precision requirement.This paper uses the shortest path ray tracing algorithm and the improved simultaneous iterative reconstruction techniques（SIRT） to fnd the result in 2 d plane ，and compares the results to- that got with the traditional single hole method so as to understand the reliability，practicality and accuracy of wave velocity test method in this article.

Keywords：shortest path ray tracing；SIRT algorithm；puckering method

收稿日期：2015-07-15

DOI:10.11921/j.issn.2095-8382.20160206

中图分类号：TP319

文献标识码：A

文章编号：2095-8382（2016）02-024-06