铣削加工工艺力学机理研究*

（西北工业大学机电学院，西安 710072）

金属铣削加工过程中的影响因素很多，比如切削参数、刀具几何参数以及工件、刀具材料等，这也使得新加工工艺的开发和切削条件的优化变得异常复杂。传统上，铣削过程中常采用试错法选取合理的工艺参数以保证加工精度。然而，试错法成本高、周期长，缺乏可操作性与量化分析，已经远远不能满足市场竞争的要求。开展基于切削物理机理的建模仿真技术研究，从理论上给出指导工艺参数选择的方法，能有效解决上述问题。因此，关于切削过程机理及建模仿真研究工作也引起了国内外学者的广泛关注。加拿大英属哥伦比亚大学Altintas教授团队[1]围绕该主题进行了系统而深入的研究工作，取得的许多原创性成果得到了国内外学者广泛采用。国内西北工业大学、北京航空航天大学、南京航空航天大学、山东大学、大连理工大学等高校也在相关领域进行了深入研究，取得了许多积极有益的成果。本文将对铣削力建模、动力学建模与稳定性分析及变形误差预测与控制等工作进行介绍，以期使读者对铣削加工建模仿真技术有较系统的认识。

铣削力建模方法

铣削力建模是所有铣削加工物理仿真的核心基础。现有铣削力模型大致可以分为两类：经验模型与理论模型。经验模型是通过大量切削试验，对所测得的数据用数学方法进行处理得到的。如Fuh[2]、Abou-El-Hossein[3]借助大量的试验，利用统计学原理建立了切削力经验模型。由于经验模型需要进行大量试验，且通用性较差，因此理论模型得到了更多的关注。理论模型是基于切削工艺几何分析，经过一系列力学推导得到的切削力函数。20世纪60年代，Koenigsberger和Sabberwal[4]建立了一种切削力理论模型，该模型认为整个切削物理过程发生在剪切区域，工件材料在剪切区域发生剪切滑移产生的力即为整个切削力，因此切削力表达为与切屑载荷的比例函数，而比例系数则命名为切削力系数。之后，许多学者对该模型进行了发展和延拓，形成了经典的铣削力学模型（Mechanical Model）[1]，这里简述如下:

圆柱坐标系下的切削力可以表达为切削力系数（KT、KR、KA）与切削载荷的乘积，如下式：

式中，FT、FR和FA分别代表刀具切向、径向和法向切削力；h代表瞬时未变形切屑厚度；b代表轴向切深。显然，h、b取决于工艺参数，容易计算得到。因此，要计算切削力，关键是确定切削力系数。目前，关于切削力系数的确定主要有两组方法，一种是直接标定切削力系数，如Altintas[1]提出的用固定径向、轴向切深与转速，改变进给率的方法标定切削力系数，但该方法通用性不强，当刀具几何参数改变时，需要进行重新标定；另一种是通过正交与斜角切削几何关系，建立切削力系数与刀具几何和材料属性参数表达式，通过计算得到切削力系数，即通过几何关系将切削力系数转化成剪切角（φn）、摩擦角（βn）、剪切应力（τs）、刀具法向前角（αn）、刀具螺旋角刀（β）和切屑流动角（η）的函数：

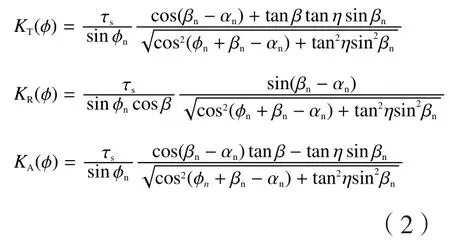
上式中的刀具几何参数可以测得，切屑流动角近似等于刀具螺旋角，因此只有剪切角（φn）、摩擦角（βn）、剪切应力（τs）需要进行标定。在Altintas[1]提出的模型中，需要180组车削试验来确定以上3个参数。本节简要给出作者提出的快速铣削标定算法[5]。

图1 铣削过程示意图Fig.1 Diagram of milling process

图1给出了铣削过程示意图[5]，在建模求解铣削力时，首先将铣刀沿轴向离散为许多微分单元，然后通过积分得到切削合力。图1中i和j分别表示刀齿编号和微分单元编号。由斜角切削几何关系有：

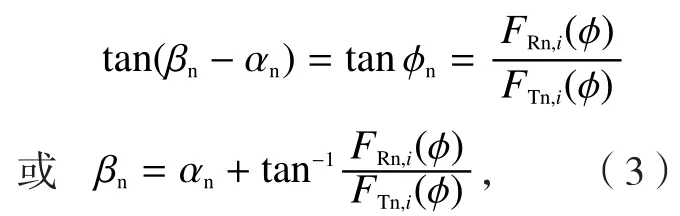
式中，FRn,i(φ)为刀具第i个刀齿切削刃的法平面内切向力，FTn,i(φ)为刀具第i个刀齿的切削刃的法平面内的进给力，显然，通过试验测定相关切削力即可按式（3）标定得到摩擦角。需要说明的是测力仪测定切削力一般为笛卡尔坐标系下（即X、Y、Z方向）测力值，还需进行坐标变换得到FR和FT，详细方法参考文献[5]。剪切角的标定基于最大剪应力理论，即剪切速度方向和合力方向成45°角。结合斜角切削几何关系，有：

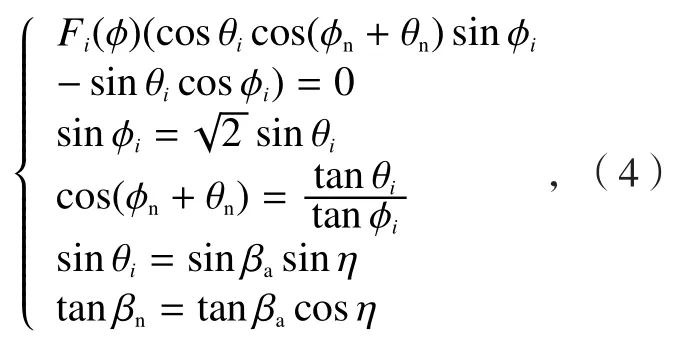
上式相关参数定义同文献[5]，解式（4）即可得到剪切角。确定了θi、θn和φi等角度，依据计算公式求解剪切应力如下：

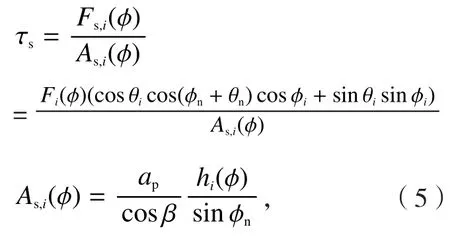
该模型由于标定了求解切削力系数所需的物理参数，在刀具变化时，只需将相关刀具几何参数代入式（2）计算即可，因此，该模型对于任何几何刀具具有普遍适用性。

也有学者将上述铣削力模型称为集成模型或一元模型。相应地，将同时考虑了切削过程中的剪切效应和犁切效应（即将切削力表达为犁切力和剪切力两项和的形式）称为二元模型。在此基础上，作者还提出了考虑底刃在切削过程中对切削力的作用的模型，即三元模型[6]。此外，作者还首次提出了铣削力可以表达为名义量与偏心引起的扰动量的叠加，并可以利用名义量来标定切削力系数，扰动量标定偏心参数。更多关于铣削力建模方面的工作，读者可以参考文献[7-10]。

铣削过程动力学建模

颤振是金属切削加工过程中的一种较易发生、由切屑厚度动态再生引起的自激振动，也是导致切削失稳的最主要因素。铣削过程颤振极易诱发刀具快速磨损、低精度波纹加工表面、噪音污染，还会严重影响机床寿命。因此，铣削颤振的动力学机理研究具有十分重要的学术和应用价值。要对铣削工艺系统进行动力学建模分析，首先要获得工艺系统动力学特性，然后才能求解在切削力的激励下，系统动力学响应规律。因此，本节将阐述两方面内容，一是刀尖频响建模预测方法，即工艺系统动力学特性的确定；另一方面，还将对颤振稳定性预测方法进行介绍，即系统动力学响应规律。

1 刀尖频响建模方法

目前，工艺系统动力学特性的确定主要有模态试验和建模计算两条主要途径。由于实际生产中，一个零件加工过程往往选用多种刀具和刀柄组合，显然试验法更适用于实验室，生产单位则更需要一套高效计算的方法。下文将介绍作者提出的一种适用于各种旋转刀具的通用刀尖频响建模思想[11]。

如图2所示[11]，刀具-刀柄-主轴组合结构被分解成为4个子结构，最终刀尖点频响是通过各子结构动态响应组合来获得的。其中，SHS代表主轴-刀柄子结构，STC代表刀具无刃杆部单元，FPTC代表刀具刃部单元，THJIC代表刀具-刀柄连接接触单元。这里，刀具-刀柄被当成零厚度阻尼弹性层。对于主轴-刀柄子结构，首先将其分为NH个节点连接的（NH-1）个等长单元，则对该子结构有：QH(ω)=HH(ω)FH-TH(ω)；其中，HH(ω)可以通过响应耦合子结构法求得。在获得主轴-刀柄子结构频响后，依次对其他几个单元进行求解，最终组合得到刀尖点频响结果。详细求解信息，请参考文献[11]。

2 颤振稳定性预测方法

Tobias[12]等率先提出了应用稳定性叶瓣图（Stability Lobe）来表征车削过程稳定切削域，并为后续研究者广泛采用以开展稳定性分析工作。Altintas[1]指出连续的切削表面之间的相位移动引发指数增长的切屑厚度是诱发切屑再生颤振的根本原因，并提出了经典的频域求解稳定域零阶算法，同时对该算法进行了许多后续完善。除频域法外，许多学者还从时域研究了稳定性预测问题，其中比较具有代表性的是匈牙利学者Insperger提出的半离散算法（Semi-Discretization Method）[13]。但是，该方法在提出时是基于理想工艺系统的，无法应用于刀具偏心等引起的多延时问题。对此，Wan等[14]基于半离散法提出了一种通用多延时铣削稳定性预测方法。随后，又将该算法推广到预测多模态铣削系统[15]。下文给出该方法的基本思想。

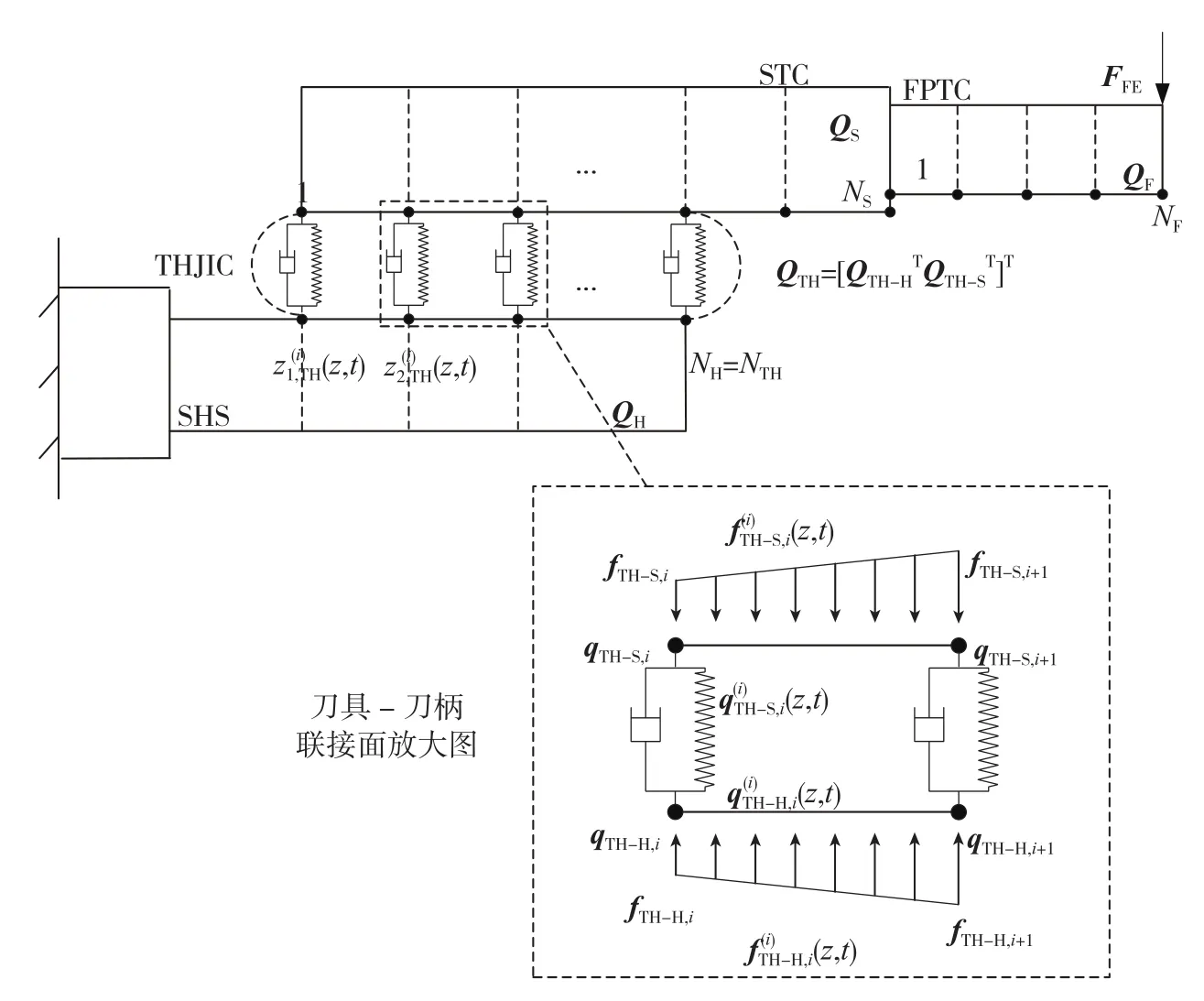
图2 刀具-刀柄-主轴装配建模原理图Fig.2 Principle view of tool-holder-spindle assembly modeling

在铣削过程中，根据Altintas专著[1]中的定义，将关联第j阶模态在t时刻X、Y方向的刀具动态变形记作xj(t)和yj(t)。相应地，第v个刀齿、第u个轴向单元径向位移（或沿切屑厚度方向的位移可以表达为：

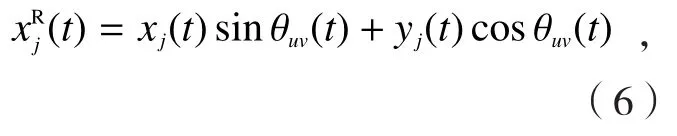
时间延时量τl对应的动态切屑厚度为：

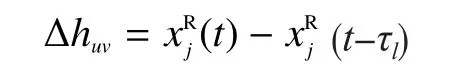
时间延时量的定义及确定方法参考文献[14]。动态切屑厚度导致的动态切削力（FdX,j,uv(t),FdY,j,uv(t)），可以表达为：

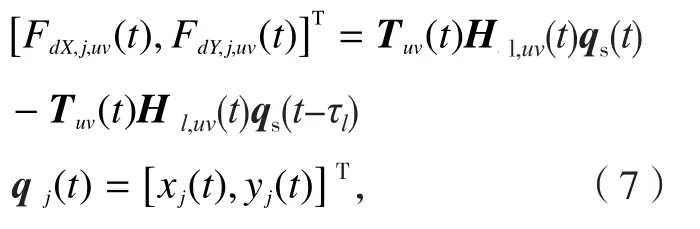
其中，

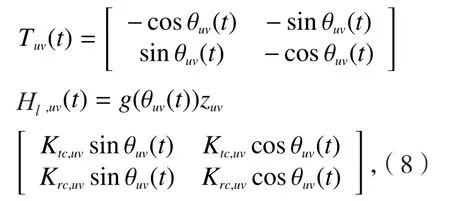
进而，基于模态叠加原理，构建多模态多延时稳定性控制方程，

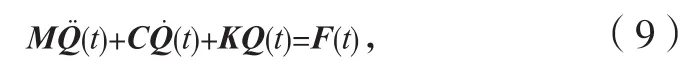
其中，

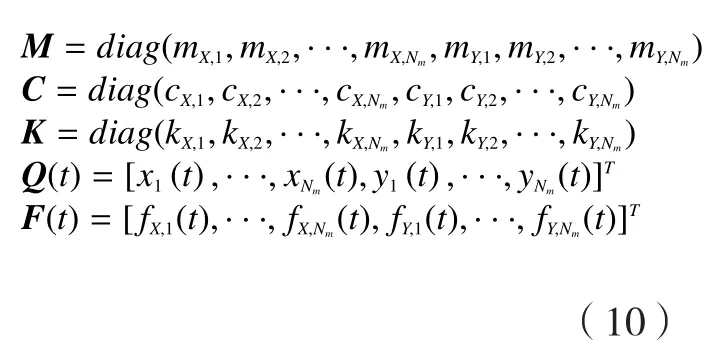
式中，diag（*）代表对角矩阵运算，Nm表示主导模态数，ma,j、ca,j和ka,j分别表示a方向（a=X或Y）第j阶模态下的模态质量、阻尼系数和模态刚度。当Nm等于1时，上述问题转化为单模态问题，文献[14]对于该问题求解进行了详细论述，并对刀具几何、进给等对稳定性影响规律进行了深入研究讨论。对上式，采用半离散算法求解，即可获得稳定性叶瓣图，更多信息可参考文献[15]。由于该问题在求解时计算时间成本过高，作者还对该方法进行了改进，提出了一种最低包络线的快速算法，并理论证明了该方法，同时对其适用性进行讨论，这里不再赘述。图3给出了多延时系统预测的应用实例[14]。

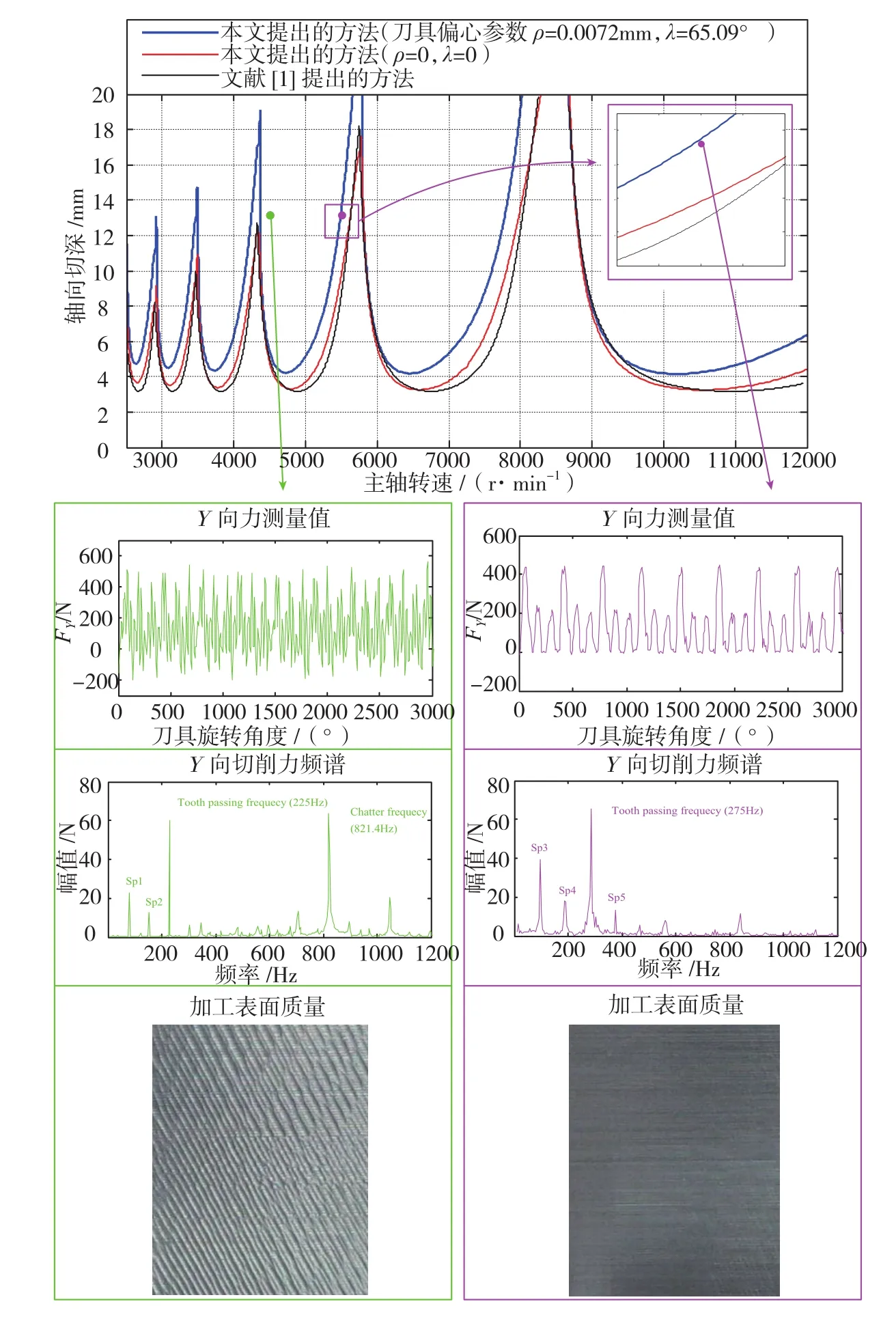
图3 多延时铣削系统稳定性结果Fig.3 Stability results for milling system with multiple delays

变形误差预测与控制

1 变形误差预测

加工过程中，由于切削力的作用，刀具和工件均产生弹性变形。走刀过后变形弹性恢复，致使部分材料残留而未被切除，造成了零件表面的加工误差。Kline指出，沿被加工面法向的分力是决定工件表面误差的主要因素[16]。目前，对于无颤振的静态周铣加工过程表面误差的研究，主要有3类模型：（1）刚性模型，直接用名义切削量预测切削力，不考虑刀具及工件变形对加工过程的反馈影响，也不考虑材料去除引起的工件刚度变化的影响；（2）定刚度柔性模型，此模型相对刚性模型，在预测切削力时考虑刀具及工件变形的反馈影响，但不考虑材料去除引起的工件刚度变化的影响；（3）变刚度柔性模型，顾名思义，其预测切削力不仅考虑刀具/工件变形的反馈影响，而且还要考虑材料去除引起的工件刚度变化的影响。这里简要介绍作者提出的一种基于商用软件SAMCEF，同时考虑工件与刀具变形影响和材料去除引起刚度变化的算法[17]。

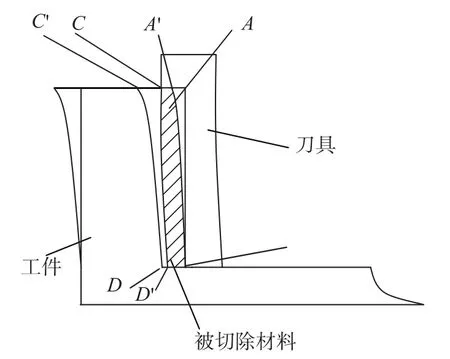
图4 薄壁零件铣削加工示意图Fig.4 Diagram of thin-walled workpiece milling process

如图4所示[18]，使用平头立铣刀铣削薄壁面AB，应该切除阴影部分ABDCA，但由于切削力的作用，使刀具和工件均产生弹性变形，A、C和D点分别移到A'、C'和D'点，致使加工过程中的实际切削量（如径向切削量）小于名义值，走刀过后变形弹性恢复，从而残留部分材料未被切除，造成板厚方向的加工误差。

变形误差ep可表达为：

式中，δw为工件变形，δc为刀具变形。

刀具变形按悬臂梁理论计算，同时假设刚性主轴与夹头中刀柄装夹部分间为线弹性关系，即存在装卡刚度。在某加工瞬态，刀齿节点（i，j）受作用于刀齿节点（k，m）的切削力而引起的静态弹性变形可计算为：

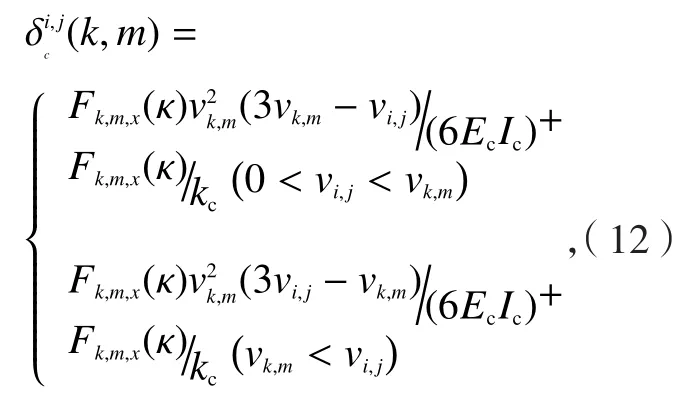
式中，Ec表示刀具杨氏模量，Ic表示铣刀截面对其形心轴的惯性矩，kc表示刀具与夹头间的装卡刚度，表示铣刀装卡后的悬臂长度。沿着刀具轴向对所有刀齿变形求和即可得到所有刀齿节点受力在刀齿节点（i，j）引起的变形。

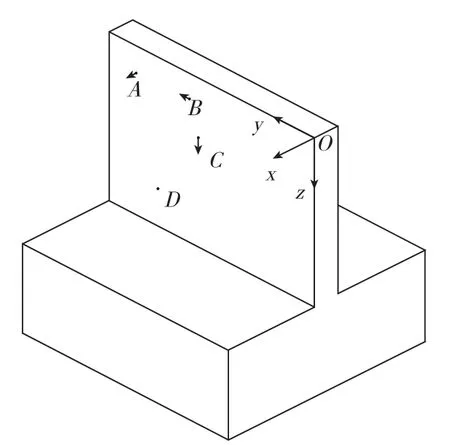
图5 工件变形计算Fig.5 Calculation of workpiece deformation

工件加工过程中，影响加工精度的主要是工件弹性变形引起的，对工件变形的计算采用单位载荷法。如图5所示[8]，若在A点、B点和C点分别加X方向、Y方向和Z方向的单位载荷，它们在D点X方向引起的变形分别为δ(AX,D,x)和δ(BY,D,X)和δ(CZ,D,X)，那么当作用于A点X方向、B点Y方向和C点z方向的实际载荷为别为F(AX)、F(BY)、F(CZ) 时，D点X方向的变形大小为

刀具/工件变形的反馈影响按定刚度柔性模型中介绍的方法进行考虑。对材料去除引起的工件刚度变化，借鉴结构拓扑优化设计中的密度变量思想，考虑在恒定网格下修改被去除网格单元刚度的方法，实现对工件刚度的修正。

对于工件某网格单元i，如果有材料已被切除，采用下式对其刚度进行修正：

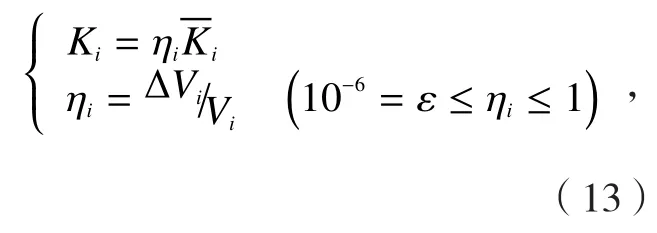
式中表示工件单元i的名义刚度，ΔVi表示该单元i被切削后的剩余体积，Vi表示该单元i被切削前的实际体积。如果ΔVi=0，则取ηi=ε,取10-6=ε≤ηi是为了避免单元刚度矩阵的奇异性。更多详细内容，读者可参阅文献[17-19]。

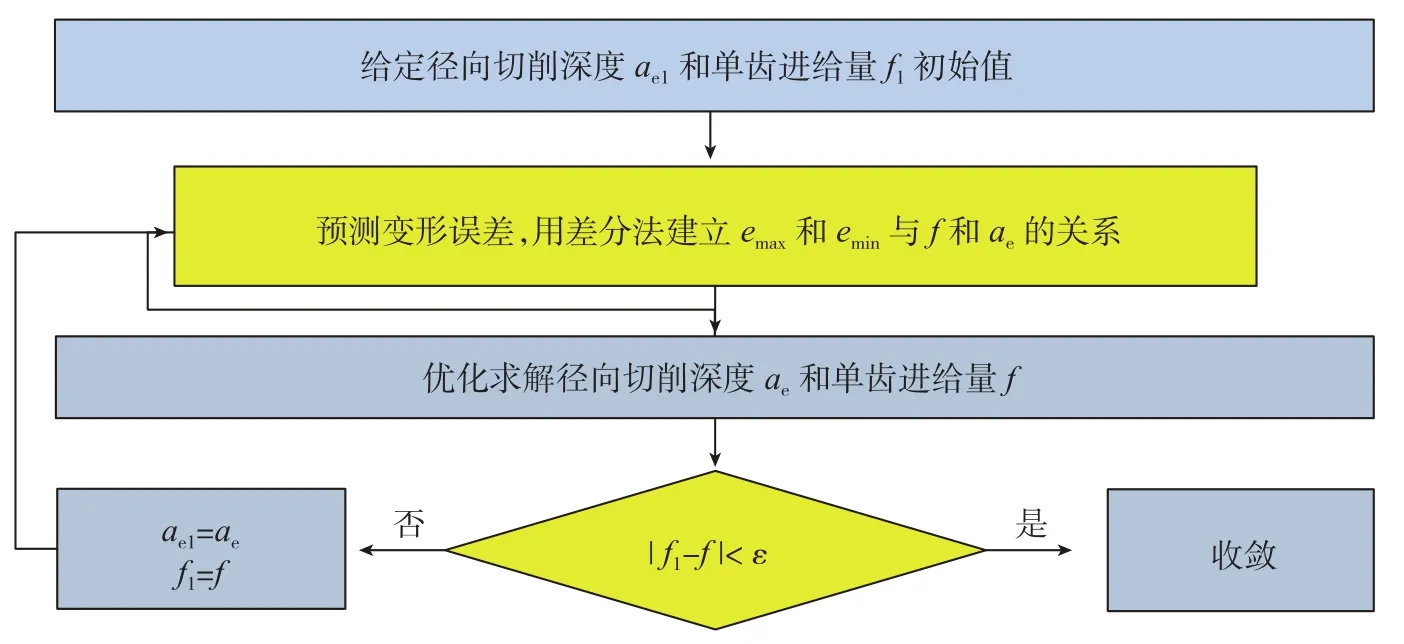
图6 双参数误差控制方法计算流程Fig.6 Optimization algorithm for surface form error control

2 变形误差控制方法

当预测变形误差超过预设公差要求时，需对变形误差进行控制。镜像补偿法，即采用镜像对称原理对径向切削深度进行偏置补偿的方法，广泛用于变形误差控制，其主要原理为：将名义径向切削深度沿加工变形反方向偏移一个大小为变形量e的距离，可以实现减小变形误差的目的。需要指出，这种方法虽然可以减小变形误差,但不能保证补偿后的变形误差落在公差带范围内。

为解决此问题，作者提出了一种双参数优化方法，即通过同时优化单齿进给量f与径向切削深度ae，在维持生产率的同时实现最终误差控制在公差带范围的目的，其数学模型可表达如下：

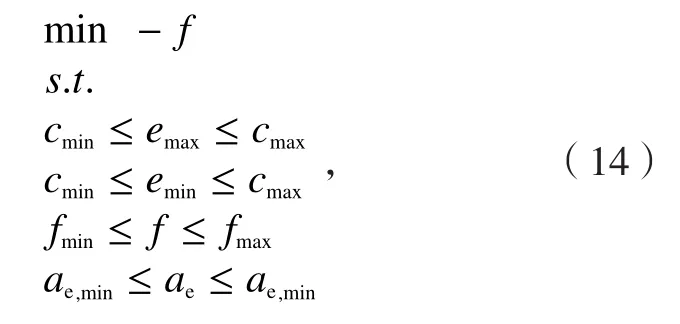
式中，emax和emin为给定单齿进给量与径向切削深度下变形误差的最大值和最小值，cmax和cmin为给定变形误差上下限，fmax和fmin为单齿进给量上下限，ae,max和ae,min为径向切削深度上下限。优化求解式（14）的流程如图6所示[20]，可以看出，求解的关键步骤之一是建立emax和emin与f和ae的关联关系。

关于求解式（14）以及如何建立emax和emin与f和ae的关联关系的详细内容，请参见文献[20]。

结论

本文系统地介绍了铣削加工过程物理仿真的几大关键技术问题，涵盖了从切削力建模、变形误差预测到工艺系统动力学建模与颤振稳定性分析等多方面内容，以期使读者能够较全面了解基于切削工艺力学机理的建模仿真技术。

[1]ALTINTAS Y.Manufacturing automation[M].Cambridgeshire: Cambridge University Press, 2012.

[2]FUH K-H, HWANG R-M.A predicted milling force model for high-speed end milling operation[J].International Journal of Machine Tools and Manufacture, 1997, 37(7):969-979.

[3]A B O U-E L-H O S S E I N K,KADIRGAMA K, HAMDI M, et al.Prediction of cutting force in end-milling operation of modified AISI P20 tool steel[J].Journal of Materials Processing Technology, 2007, 182(1): 241-247.

[4]KOENIGSBERGER F, SABBERWAL A J P.An investigation into the cutting force pulsations during milling operations[J].International Journal of Machine Tool Design and Research, 1961, 1: 15-33.

[5]WAN M, PAN W J, ZHANG W H, et al.A unified instantaneous cutting force model for flat end mills with variable geometries[J].Journal of Materials Processing Technology, 2014, 214(3):641-650.

[6]WAN M, LU M S, ZHANG W H, et al.A new ternary-mechanism model for the prediction of cutting forces in flat end milling[J].International Journal of Machine Tools and Manufacture, 2012, 57: 34-45.

[7]WAN M, ZHANG W H, DANG J W, et al.New procedures for calibration of instantaneous cutting force coefficients and cutter runout parameters in peripheral milling[J].International Journal of Machine Tools and Manufacture, 2009, 49:1144-1151.

[8]WAN M, ZHANG W H.Systematic study on cutting force modelling methods for peripheral milling[J].International Journal of Machine Tools and Manufacture, 2009, 49:424-432.

[9]WAN M, ZHANG W H, TAN G, et al.An in-depth analysis of the synchronization between the measured and predicted cutting forces for developing instantaneous milling force model[J].International Journal of Machine Tools and Manufacture, 2007,47: 2018-2030.

[10]WAN M, ZHANG W H, QIN G, et al.Efficient calibration of instantaneous cutting force coefficients and runout parameters for general end mills[J].International Journal of Machine Tools and Manufacture, 2007,47:1767-1776.

[11]YANG Y, ZHANG W H, MA Y C,et al.Generalized method for the analysis of bending, torsional and axial receptances of toolholder-spindle assembly[J].International Journal of Machine Tools and Manufacture, 2015, 99:48-67.

[12]TOBIAS S A.Machine tool vibration[M].New York: Blackie and Sons Ltd,1965.

[13]INSPERGER T, STEPAN G.Updated semi-discretization method for periodic delaydifferential equations with discrete delay[J].International Journal for Numerical Methods in Engineering, 2004, 61: 117-141.

[14]WAN M, ZHANG W H, DANG J W, et al.A unified stability prediction method for milling process with multiplt delays[J].International Journal of Machine Tools &Manufacture, 2010, 50(1): 29-41.

[15]WAN M, MA Y C, ZHANG W H,et al.Study on the construction mechanism of stability lobes in milling process with multiple modes[J].International Journal of Advanced Manufacturing Technology, 2015,79:589-603.

[16]KLINE W A, DEVOR R E,SHAREEF I A.The prediction of surface accuracy in end milling[J].Journal of Engineering for Industry-Transactions of the ASME, 1982,104: 272-278.

[17]WAN M, ZHANG W H, QIU K P,et al.Numerical prediction of static form errors in peripheral milling of thin-walled workpieces with irregular meshes[J].Transactions of the ASME Journal of Manufacturing Science and Engineering, 2005, 127: 13-22.

[18]万敏.薄壁件周铣加工过程中表面静态误差预测关键技术研究[D].西安: 西北工业大学, 2005.

WAN Min.Numerical prediction of static form errors in the peripheral milling of thinwalled workpiece[D].Xi’an: Northwestern Polytechnical University, 2005.

[19]WAN M, ZHANG W H.Efficient algorithms for calculations of static form errors in peripheral milling[J].Journal of Materials Processing Technology, 2006,171:156-165.

[20]WAN M, ZHANG W H , QIN G H, et al.Strategies for error prediction and error control in peripheral milling of thin-walled workpiece[J].International Journal of Machine Tools and Manufacture, 2008, 48: 1366-1374.