速率稳定平台隔离度的研究与应用

（中国空空导弹研究院，洛阳 471009）

近年来，稳定平台技术被广泛应用于军事领域，如飞机、导弹、舰船等，其主要功能为隔离载体扰动，保持稳定平台相对惯性空间稳定。

隔离度是反映稳定平台对载体扰动的隔离能力，是稳定平台的重要性能指标。隔离度定义为在载体扰动作用下，稳定平台响应角速度有效值与载体运动角速度有效值之比。隔离度大小直接影响稳定平台惯性空间稳定性，因此，建立准确的隔离度模型对提高稳定平台稳定性有实际的意义。

1 模型推导与建立

1.1 电机及负载模型

鉴于直流力矩电机低转速、大力矩且可直接与负载耦合等优点，采用直流力矩电机直接驱动平台运动。直流力矩电机工作原理与普通直流伺服电动机一样，电机及负载模型如图1所示。

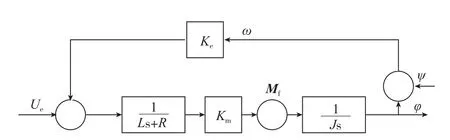
图1 电机及负载模型Fig.1 Motor and load model

式中，R、L、Ke、Km、ue、φ和ω分别为直流力矩电机电阻、电感、反电势系数、力矩系数、输入电压、绝对角速度和相对角速度，J为电机及负载等效转动惯量，Mf为摩擦力矩，ψ为载体扰动角速度。

1.2 传感器及处理电路模型

速率稳定平台采用速率陀螺作为角速度测量元件，与处理电路等效为一阶惯性环节：

式中，Kg为放大倍数，τ为时间常数。

1.3 功率放大模型

采用PWM驱动直流力矩电机，其模型简化为纯比例环节Kpwm。

1.4 摩擦力矩模型

摩擦力矩是影响稳定平台隔离度重要因素，因此建立准确的摩擦力矩模型是建立稳定平台隔离度模型和系统设计的关键。

目前工程中常采用摩擦力矩模型（包括库仑摩擦模型、库仑+粘滞摩擦模型、静摩擦+库仑+粘滞摩擦模型和Stribeck摩擦模型）。

鉴于低速下摩擦力矩的变化直接影响到稳定平台隔离度的大小，Stribeck摩擦模型能准确描述低速下摩擦力矩变化情况，本文采用Stribeck摩擦模型，其数学模型为：

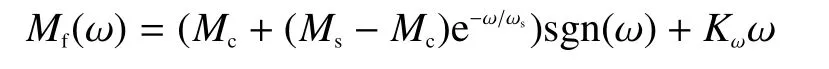
式中，Ms、Mc、ω、ωs和Kω分别为静摩擦力矩、库仑摩擦力矩、相对角速度、临界Stribeck平台角速度和粘滞摩擦系数。

测试稳定平台不同转速下摩擦力矩大小，采用模式识别的方法估算得到Stribeck摩擦模型为：

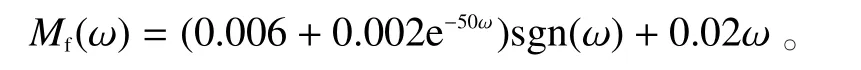
1.5 载体扰动模型

载体扰动模型一般用正弦运动来模拟，其数学模型为ψ=Asin(ωt)。在隔离度模型建立和仿真中，用载体扰动角速度ψ来实现。

1.6 稳定平台隔离度模型

根据以上推导模型，建立基于惯性坐标系的速率稳定平台隔离度模型，如图2所示。

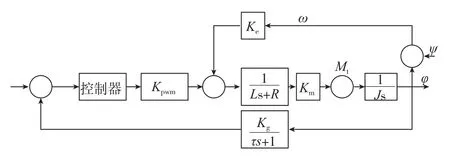
图2 平台隔离度模型Fig.2 Model of platform disturbance rejection

2 控制系统设计

稳定平台控制系统设计要求包括稳态精度高、响应速度快，稳定裕度大和隔离效果好等。鉴于频率分析法物理意义明确、简便、同时兼顾动态响应和噪声抑制等优点，本文采用连续系统频域分析法进行稳定平台控制系统设计。

根据以上推导模型，稳定平台控制系统开环传递函数为为 了 满足稳定平台稳态精度高的要求，同时保证控制系统动态性能和抑制高频噪声等，校正后控制系统开环幅频特性曲线采用“1-2-1-2”型，其控制器设计为以下简称控制器 1）。为了进一步提高稳定平台控制系统低频开环增益，同时不改变控制系统动态性能等，结合串联滞后校正的特点，在控制器1基础上在低频段增加滞后校正，其控制器设计为以下简称控制器 2）。

基于控制器1和控制器2设计的稳定平台控制系统开环频率特性曲线如图3所示。

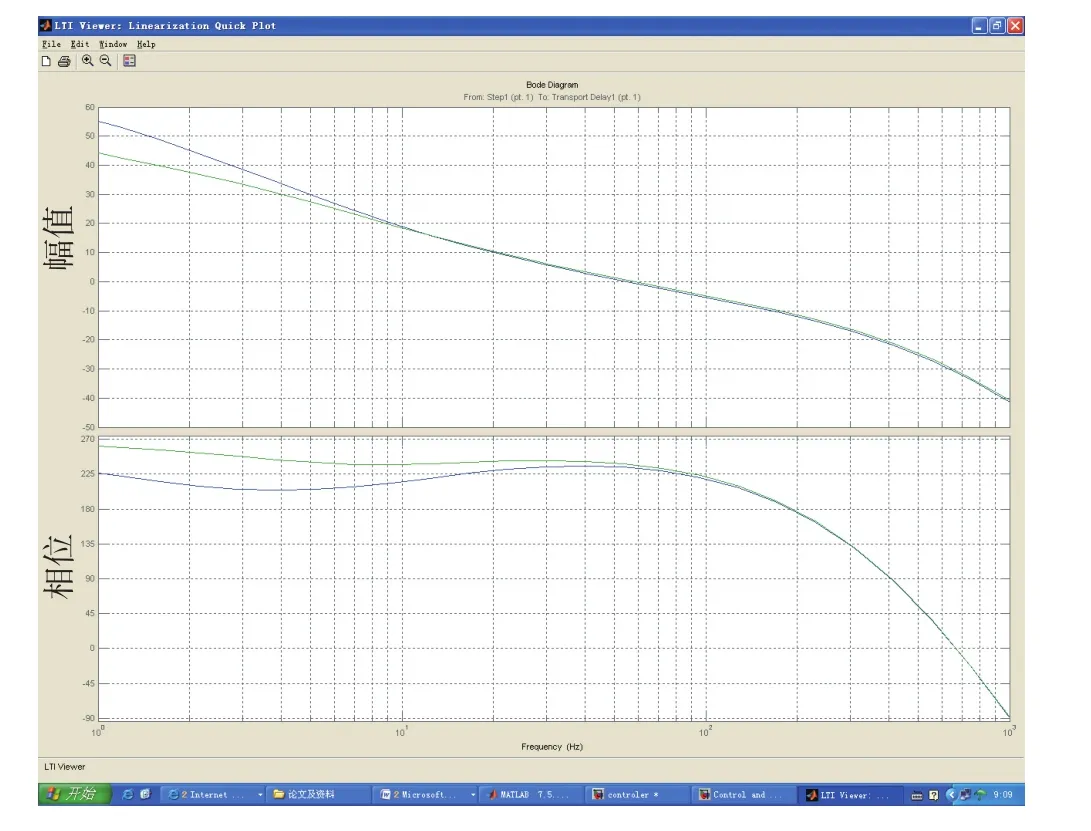
图3 伯德图Fig.3 Bode diagram

由图3得到：基于控制器1设计的稳定平台控制系统相角裕度为57°（在58Hz处），幅值裕度为11dB（在194Hz处），在2Hz处开环增益为37.5dB，在3Hz处开环增益为33.3dB；而基于控制器2设计的稳定平台控制系统相角裕度为54°（在55Hz处），幅值裕度为11dB（在191Hz处），在2Hz处开环增益为45.1dB，在3Hz处开环增益为38.5dB。控制器2相对于控制器1来说，在相角裕度和幅值裕度基本不变且满足稳定平台控制系统设计要求情况下，大幅度地提高稳定平台控制系统低频开环增益。

3 仿真与试验验证

3.1 隔离度仿真

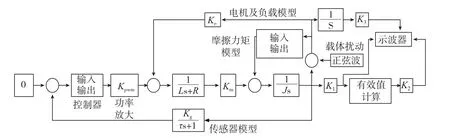
图4 隔离度仿真模型Fig.4 Simulation of platform disturbance rejection

为了验证控制器设计效果，进行隔离度仿真。首先在Matlab/Simulink中建立隔离度仿真模型，如图4所示。在隔离度仿真中，摩擦力矩模型通过调用Matlab/Simulink中的Embedded MATLAB Function模块，编写程序实现的；载体扰动用载体运动角速度施加，通过对载体扰动求导计算得到载体运动角速度；调用Matlab/Simulink中的RMS模块计算稳定平台隔离度。

利用Matlab/Simulink中的RMS模块计算稳定平台在控制器1和控制器2作用下的隔离度分别为2.51%和1.72%。从计算结果看，控制器2相对于控制器1来说，提高稳定平台隔离度达到30%以上。

3.2 试验验证

为了更好地验证控制器设计效果，进行稳定平台隔离度测试试验。用摇摆台模拟载体正弦扰动，测试稳定平台在控制器1和控制器2作用下的隔离度分别为2.72%和1.96%。由试验数据得：控制器2相对于控制器1来说，提高稳定平台隔离度达到28%，虽然比仿真结果略小，但是考虑稳定平台其他干扰力矩的影响，与实际相符[1-11]。

4 结 论

本文推导了速率稳定平台隔离度模型，阐述了摩擦力矩模型在隔离度仿真中应用，改进控制器设计，提高稳定平台隔离度，并进行隔离度仿真和产品实验验证，给出一个提高稳定平台隔离度方法，可为实际速率稳定平台控制系统设计提供借鉴。

[1]秦继荣，沈安俊.现代直流伺服控制技术及其系统设计[M].北京：机械工业出版社，2002.

QIN Jirong，SHEN Anjun.Modern servo control technology and system design[M].Beijing： China Machine Press ，2002.

[2]胡寿松.自动控制原理 [M].北京：科学出版社，2001.

HU Shousong.Automatic control principle[M].Beijing：Science Press，2001.

[3]黄忠霖，黄京.控制系统MATLAB计算与仿真[M].国防工业出版社，2009.

HUANG Zhonglin，HUANG Jing.Calculation and simulation of the control system MATLAB [M].Beijing:National Defence Industry Press，2009.

[4]王连明.机载光电平台的稳定与跟踪伺服控制技术研究[D].长春：中国科学院长春光学精密机械与物理研究所，2002.

WANG Lianming.Study on stabilization and tracking servo control technology of airborne optoelectronic platform [D].Changchun: Changchun Institute of Optics, Fine Mehcanics and Physics, Chinese Academy of Sciences，2002.

[5]崔莹莹，夏群力，祁载康.导引头稳定平台隔离度模型研究[J].弹箭与制导学报，2006,26(1):22-25.

CUI Yingying，XIA Qunli，QI Zaikang.Research on the isolation degree model of the seeker stabilized platform[J].Journal of Missile and Missile，2006,26(1):22-25.

[6]宋韬，林德福，祁载康.平台导引头隔离度模型辨析[J].北京理工大学学报，2013(6):575-580.

SONG Tao，LIN Defu，QI Zaikang.Isolation degree model identification of platform[J].Transaction of Beijing Insititute of Technology，2013(6):575-580.

[7]姚秀娟.图像导引头稳定伺服系统隔离度分析与仿真[J].自动化应用，2013(5):54-55.

YAO Xiujuan.Isolation degree analysis and simulation of image seeker servo system [J].Automation Application，2013(5):54-55.

[8]孙高，朱明超，贾宏光，等.摩擦自适应补偿在导引头稳定平台控制系统中的应用[J].红外与激光工程，2013(5):1316-1321.

SUN Gao，ZHU Mingchao，JIA Hongguang，et al.Application of friction adaptive compensation in control system design of seeker stabilized platform [J].Infrared and Laser Engineering，2013(5):1316-1321.

[9]吕娴娜，刘银年.基于摩擦观测器的伺服控制系统研究及仿真[J].测控技术，2012,31(11):60-62.

LÜ Xianna，LIU Yinnian.Research and simulation of servo control system based on friction observer [J].Measurement and Control Technology， 2012,31(11):60-62.

[10]刘长安，周杰，郑贵林.机载稳定平台随动回路控制优化仿真研究[J].计算机仿真，2012(6):63-66.

LIU Chang’an，ZHOU Jie，ZHENG Guilin.Study on the optimization simulation of the servo loop control of the airborne stabilized platform[J].Computer Simulation，2012(6):63-66.

[11]杨蒲，李奇.三轴陀螺稳定平台控制系统设计与实现[J].中国惯性技术学报,2007,15(2):171-176.

YANG Pu，LI Qi.Design and implementation of three axis gyro stabilized platform control system [J].Journal of Chinese Inertial Technology,2007,15(2):171-176.