飞机薄壁件铆接过程变形分析与数值模拟*

（西北工业大学机电学院，西安 710072）

由于工艺过程简单、连接强度稳定可靠、检查和排除故障容易，铆接在飞机装配中得到了广泛应用[1]。在铆接力作用下，不仅铆钉镦粗变形，被连接件也因钉杆膨胀和镦头挤压产生不同程度的变形，同时，被连接件多为薄壁钣金零件，刚度小、易变形，大量的铆钉连接使薄壁件产生更加复杂的装配变形和残余应力，增加了连接结构的脆性，降低了飞机的疲劳寿命。因此，分析和研究铆接结构的变形对飞机的精准装配和使用寿命有着重要影响。影响铆接质量的参数很多，如铆接力、铆钉长度、铆钉直径、孔径公差和铆钉类型等[2]。其中铆接力的作用至关重要，不仅影响铆钉成形形状和质量，而且影响孔周残余应力应变的分布。

近年来，国内外学者在铆接方面进行了大量研究，Muller[3]利用试验和理论研究了铆接力对疲劳性能的影响，结果表明增大铆接力能够提高连接疲劳性能；Aman等[4]研究了铆接顺序、铆钉间距和被连接件之间的间隙对铆接质量的影响，得出工艺参数的优化组合能够减小铆钉和被连接件的残余应力以及被连接件之间的铆后间隙；Blanchot等[5]利用有限元模拟得出15°扇形切片模型、二维轴对称模型和三维对称模型在铆接过程中的应力应变场分布分布一致；Rijck等[6]研究认为镦头尺寸可作为飞机疲劳寿命的重要标志，其改变了被连接件受力时的应力应变场；Calvin等[7]研究了铆接结构中残余应力的形成，认为镦头的挤压增加了板料中的残余应力，并比较了普通铆钉和沉头铆钉扩张；Zhang等[8]将铆接过程中铆钉的变形分为弹性、塑性和回弹3个阶段，建立了力学模型并利用有限元进行了验证，但没考虑被连接件的变形；刘平等[9]利用主应力法将铆接过程简化为平面应变镦粗变形，建立平衡方程并计算铆接所需的镦粗力，但没涉及到铆接力对铆接变形的影响；王宇波等[10]分析了自动钻铆和手工铆接对连接件疲劳寿命的影响，比较不同工艺参数组合下的连接件寿命；张岐良等[11]对钛合金铆钉成形时镦头内温度场变化对绝热剪切带形成的影响进行数值模拟，研究表明变形时的高温区域与绝热剪切带重合。

综上，目前开展的研究大多集中于铆接参数对残余应力场分布及疲劳寿命的影响，而对铆接变形的影响研究较少。本文借助有限元软件分析铆接过程，研究不同铆接力作用下铆钉和被连接件的变形，以及被连接件接合面处的应力应变分布。

1 有限元模型

1.1 模型描述

铆接过程属于复杂的非线性过程（几何非线性、材料非线性、边界非线性），很难得到精确解。有限元技术的发展为解决铆接成形问题提供了有效途径，其正确性也得到了广泛验证。

如图1所示，铆模为平铆模，被连接件为厚度t1=t2=2.0mm的2024-T3板料，长度取L=20mm＞6R(D/2)，可忽略孔边距效应；钉孔直径D=4.1mm；铆钉为直径d=4.0mm、高度h=9.0mm的 90°标准沉头铆钉，材料为2117-T4。由于铆接结构的对称性，以及减少运算时间，分析过程中采用轴对称模型。

（1）材料模型。非线性材料2024-T3（被连接件）和2117-T4（铆钉）没有明显的塑性屈服，本构关系采用幂指数硬化模型（σtrue=K（εntrue））描述，材料性能参数见表1[1]，应力应变曲线见图2。

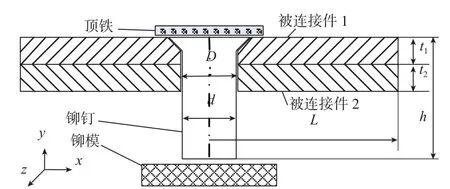
图1 铆接模型示意图Fig.1 Schematic diagram of riveting model

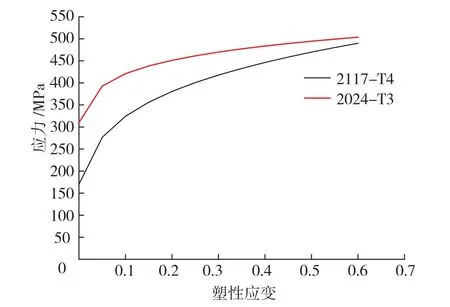
图2 材料应力应变曲线Fig.2 Stress-strain curves of material

（2）网格划分。网格采用CAX4R单元，实行畸变控制及增强型的沙漏控制；在变形较大的区域加密网格，如图3所示。

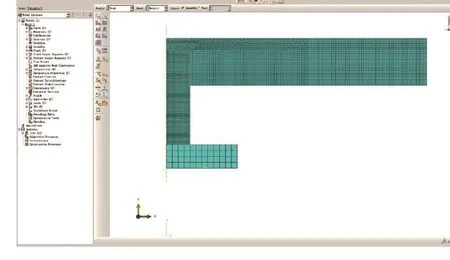
图3 网格划分、边界条件和接触设置Fig.3 Mesh generation, boundary conditions and contact settings

钉杆部分变形量大，网格尺寸小，钉头部分则较大；靠近钉孔的被连接件在铆接过程中受到挤压，产生塑性或弹性变形，采用较细的网格，较远的部分采用较粗的网格；铆模设置成刚体，铆接过程中几乎不变形，采用较粗的网格。

（3）边界条件。边界条件设置见图3，约束铆钉中轴沿X向移动，Y向和Z向的转动，约束铆钉沉头端沿Y向的移动；约束被连接件上端面沿Y向的移动和右端面沿X向移动及Z向转动；约束铆模沿Y向移动之外的约束，用于加载Y向的铆接力。

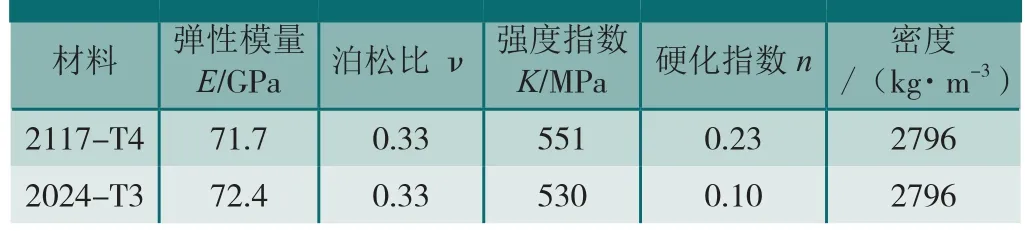
表1 2024-T3和2117-T4材料性能参数

（4）接触设置。根据主从关系设置被连接件之间、被连接件与铆钉、铆模与铆钉的摩擦，摩擦系数设置为0.2[2]。

1.2 模型验证

镦头尺寸被视为衡量铆接质量的最重要因素[6]，故采用镦头尺寸与铆接力之间的关系来验证1.1节中有限元模型。为建立铆接力与镦头尺寸之间的关系，假设：（1）铆钉与钉孔间隙为零，即没有材料通过塑性流动进入钉孔；（2）镦头形状为标准圆柱状，即钉孔外面的材料形成铆钉的镦头，铆接过程可简化如图4所示。

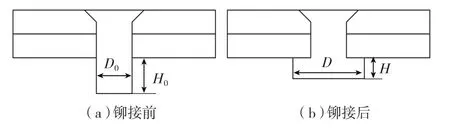
图4 铆接前后镦头尺寸变化Fig.4 Change of formed head dimension before and after riveting

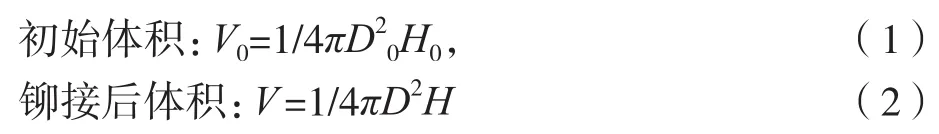
忽略进入孔内的体积，V/V0=1，由式（1）和（2）得：

铆接过程中y向挤压应力：

根据变形前后体积不变假设：

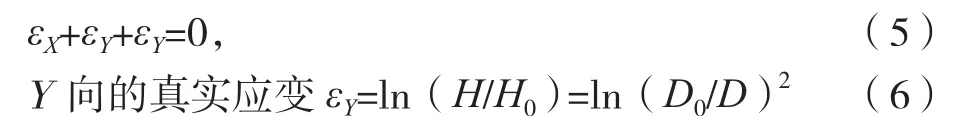
铆钉沿着Y向屈服，由幂指数硬化材料模型可得：

由方程（3）、（4）、（6）、（7）可得：

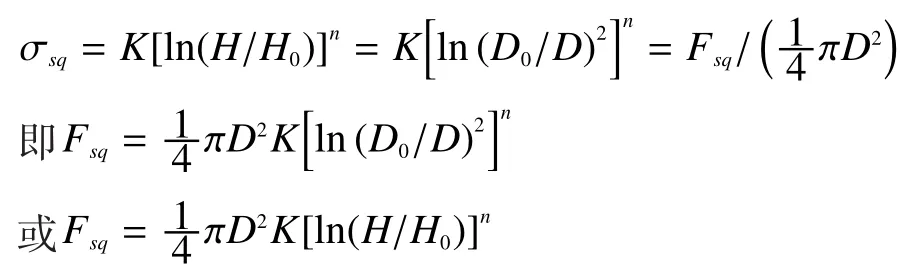
由图5、6可看出，理论模型与有限元模型吻合较好，随铆接力的增大，镦头直径和镦头高度分别接近于线性地增大和减小，与Muller等[3]得出的结论一致。从数值上看，当铆接力增大或减小时，两者误差变大，其中铆接力为8kN时，镦头直径和高度误差达到最大，分别为6.8%和8.7%，但处于可接受范围，因此1.1节中有限元模型可用于下一步分析研究。

2 数值模拟与结果讨论

2.1 铆钉变形分析

铆钉在铆模挤压和被连接件约束作用下镦粗变形，形成镦头，可根据铆钉变形时所受边界条件以及材料的弹塑性流动，将铆钉变形划分为6个阶段（图7）[12]。

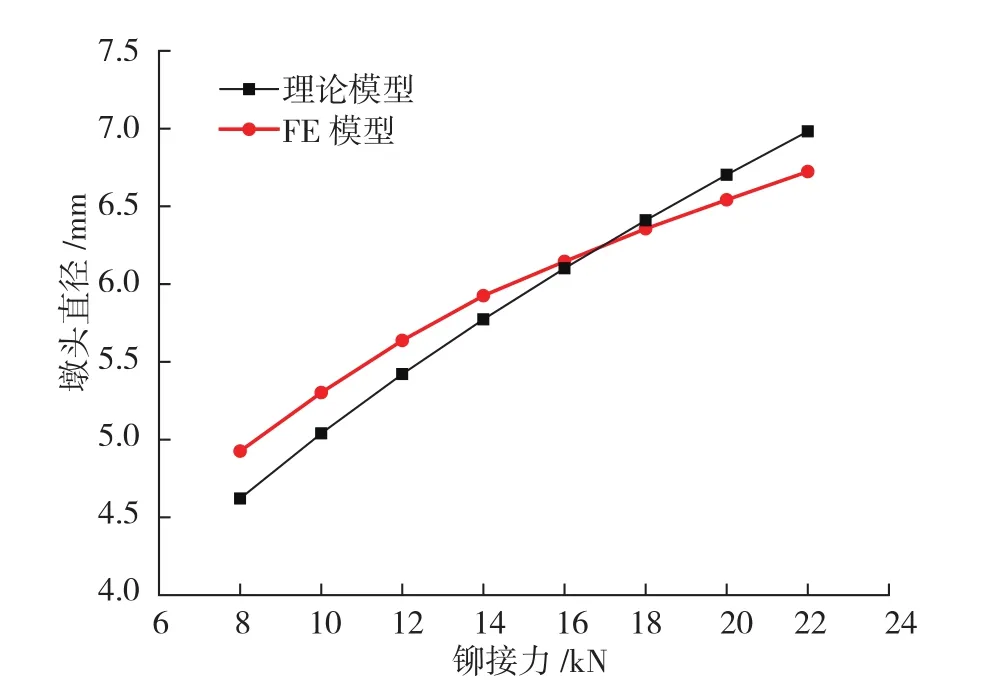
图5 铆接力与镦头直径关系Fig.5 Relation between riveting force and formed head diameter

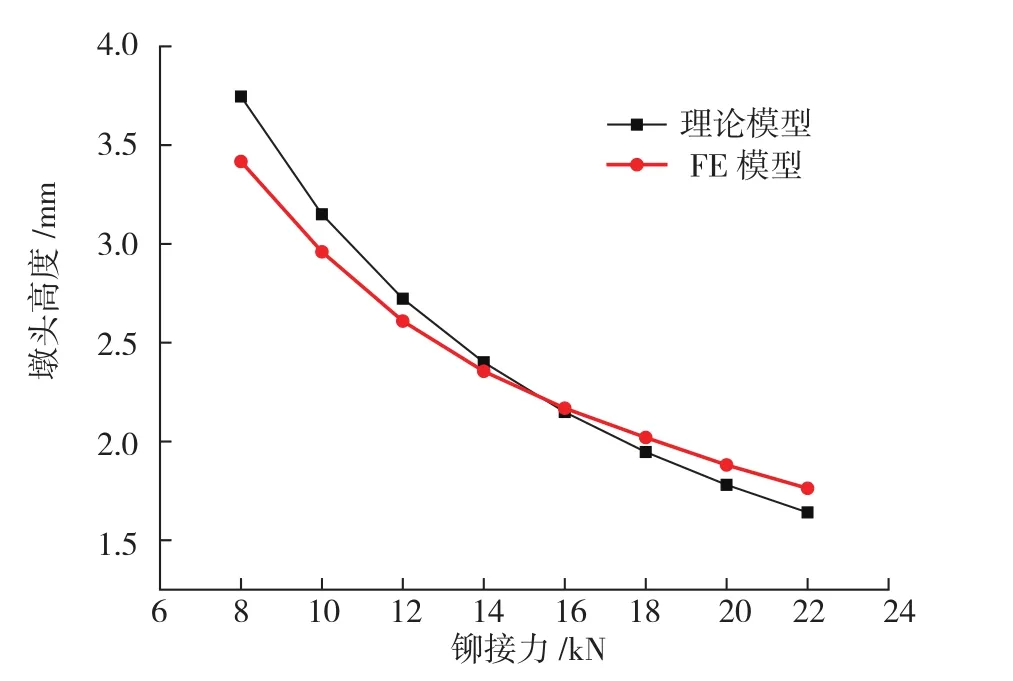
图6 铆接力与镦头高度关系Fig.6 Relationship between riveting force and formed head height

阶段1：该阶段铆钉发生弹性变形，初始阶段铆接力较小，铆钉尚未达到塑性屈服，由于加载速度快，该过程很短，铆接力在该阶段卸载时，应变恢复为零。

阶段2：该阶段从铆钉开始发生塑性变形直到铆钉与被连接件接触时结束。随着铆接力逐渐增大，铆钉应力超过弹性变形极限而产生塑性变形，同时，钉杆不断膨胀并填充孔间隙。此阶段中，铆钉尚未接触被连接件，近似为自由镦粗。如只考虑铆钉的受力变形，由于铆钉所受压力尚未传递到被连接件，被连接件不发生变形。

阶段3：该阶段从铆钉接触被连接件到铆钉与被连接件形成过盈连接时结束。随着铆钉的膨胀变形，铆钉镦头开始成形，铆钉与被连接件孔周接触面积逐渐增大，直到最后形成过盈连接。

阶段4：该阶段为铆钉镦头的形成阶段，可将铆钉的变形近似为局部镦粗。铆钉杆不仅受到铆模和被连接件孔周施加的挤压力，且铆钉材料向两侧流动逐渐接触到被连接件表面，开始受到其施加的摩擦力作用。在该阶段轴向的金属流近似趋于饱和，铆钉杆直径可近似认为不再变化，材料主要沿径向流动。

阶段5：该阶段为铆钉弹性回复阶段。第4阶段结束时铆接力达到最大，在该阶段铆模开始回撤，铆接力减小，铆钉发生弹性回复。

阶段6：铆模离开铆钉，载荷降为零，铆接过程结束。铆钉与被连接件形成干涉配合连接，由于残余应力的存在，铆钉受到被连接件的挤压力。

在铆钉上等距选取6个点，给出其轴向真实应变随时间的变化关系。

在第1阶段，各点应变变化很小，接近于零，铆钉处于弹性阶段；到第2阶段，各点应变迅速增大，开始产生塑性变形，铆钉处于自由镦粗状态；处于第3阶段时，位于铆钉孔内的点开始受到被连接件作用力，应变变化趋于平缓，而钉孔外各点处于镦头开始形成阶段，应变变化仍然很大；第4阶段为镦头成形阶段，材料主要沿径向流动，沿轴向流动可忽略不计，孔内各点应变处于平稳状态，孔外各点应变依然缓慢在增大；第5阶段各点发生了不同程度的回弹；第6阶段铆模撤去后，应变处于平稳状态。

2.2 被连接件径向变形分析

被连接件在铆接过程中受到铆钉的膨胀挤压，同时受到铆模的冲击作用，故在轴向和径向均产生变形，考虑到铆接冲击作用的偶然性，只考虑沿径向的变形。分别模拟在12kN、15kN和18kN铆接力作用下，钉孔的径向变形，如图8所示，以及15kN作用下，被连接件整体的径向变形，如图9所示。

根据图8所示，随着铆接力的增大，钉孔径向变形量增大；镦头附近的孔径扩张明显大于其他位置，但变形量沿轴向下降十分迅速，靠近钉头侧的变形量相对均匀，其中在被连接件接合处和锪窝处有起伏变化，这与被连接结构的梯度变化相关。从图9可看出连接结构的整体变形也不均匀，靠近钉孔附近的变形量大，且局限于镦头一侧。钉孔沿径向的干涉量极不均匀，对铆接结构的使用寿命产生不良影响。

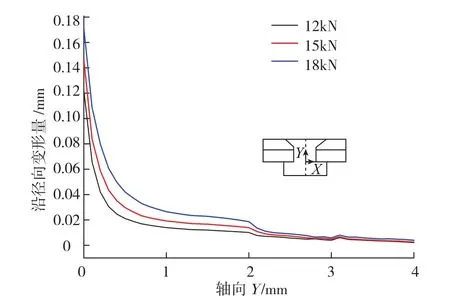
图8 钉孔轴向不同位置沿径向的变形Fig.8 Radial deformation of rivet hole along axial direction

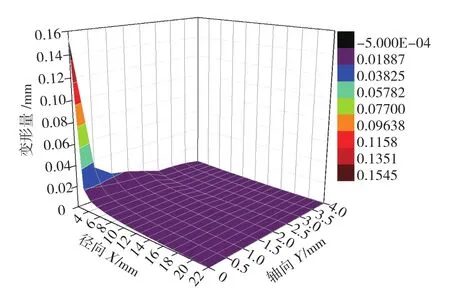
图9 被连接件截面沿径向变形Fig.9 Radial deformation of the riveting joint section

2.3 被连接件接合面应力应变分析

铆钉连接在使用中主要承受剪力，受铆钉挤压的被连接件在接合表面产生夹紧力，增大夹紧力对于上下板件通过摩擦传递载荷是非常有益的，其中铆接力是关键因素。因此，基于铆接力来研究接合面处的应力应变状态十分必要，分别模拟在 10kN、12kN、14kN、16kN、18kN铆接力作用下，接合表面的残余应力应变状态，如图10～13所示。

如图10所示，随铆接力的增大，孔边周向应力从拉应力状态变为压应力状态，应力幅值随着径向距离的增大而迅速减小，约在2.5mm位置达到最小值，随后开始增大并达到最大值，然后开始减小并趋近于0。铆接力越大，周向应力达到最大值的位置距孔边越远，大约6R（12mm）位置时，应力趋近于0。根据图11，不同铆接力作用下，接合面上的径向应力均为压应力状态，铆接力越大，径向应力达到最小值的位置距孔边越远，使径向处于某一压应力状态的临界位置远离孔边。综上，铆接力显著地改变了接合面上的应力状态，尤其是钉孔附近区域的应力状态，孔周周向应力变为压缩状态以及径向应力的减小，在一定程度上能够抵消裂纹的张应力，延迟裂纹的扩展[13]，有效改变铆接结构的连接寿命。

如图12所示，随着铆接力的增大，钉孔附近周向应变显著增大，并随径向距离增大而近线性地减小，当径向距离大于6R时，应变趋近于0，表明孔边周向应变比较集中且随径向距离变化很大。如图13所示，孔边径向应变随铆接力的增大从压应变状态变为拉应变状态，但距孔边不远，很快变为压缩状态，且铆接力越大压应变达到最小值的位置距孔边越远，当径向距离大于6R时，径向应变趋近于0。综上，铆接力显著影响接合面的应变状态，使周向和径向应变幅值增大，但影响区域仅限于孔周附近区域，距孔中心6R处，应变基本趋近于0。

图10 接合面周向残余应力分布Fig.10 Hoop residual stress distribution at the mating surface

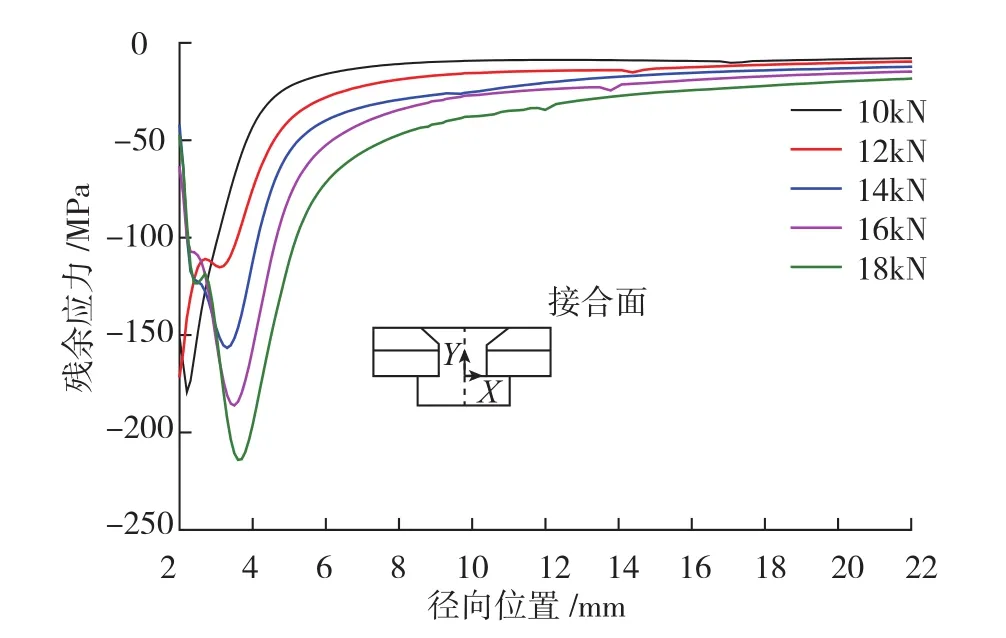
图11 接合面径向残余应力分布Fig.11 Radial residual stress distribution at the mating surface

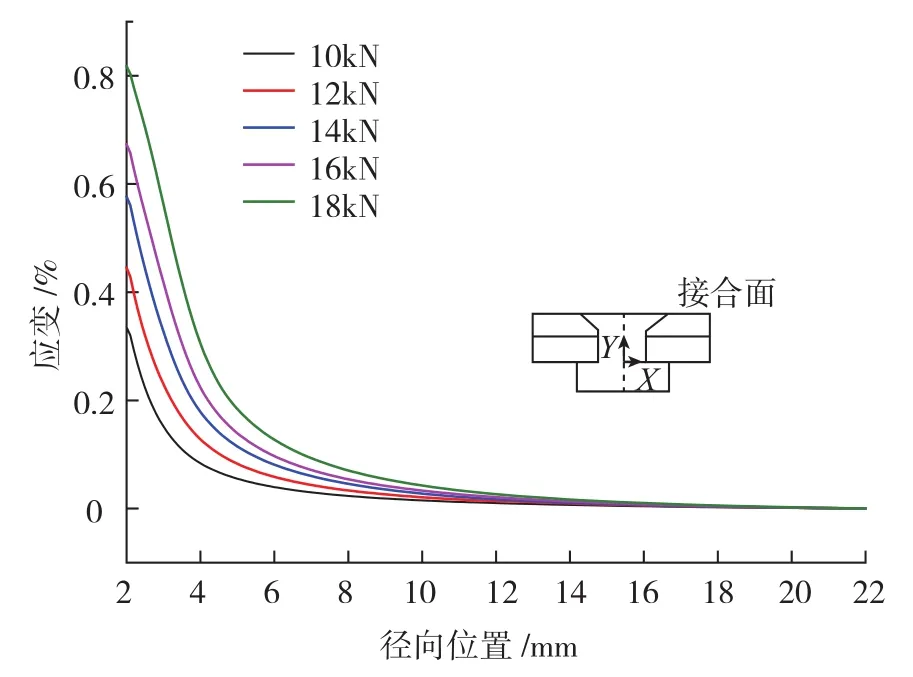
图12 接合面周向应变分布Fig.12 Hoop strain distribution at the mating surface

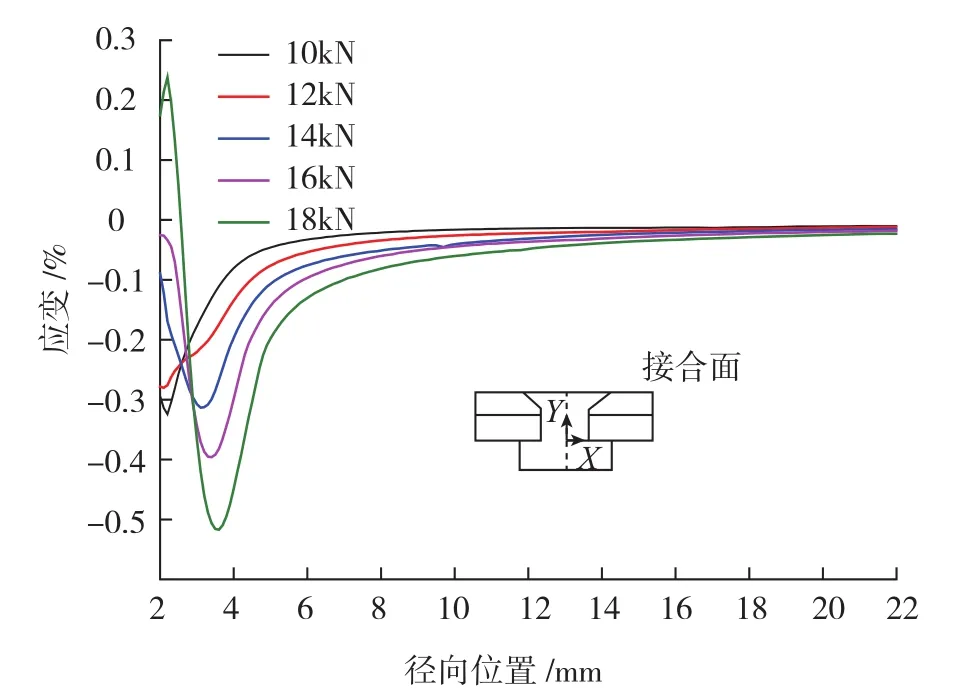
图13 接合面径向应变分布Fig.13 Radial strain distribution at the mating surface

3 结束语

本文研究了铆接过程中铆钉和被连接件的变形，以及铆接力对被连接件接合面应力应变的影响，在总结国内外相关研究的基础上，主要开展了以下工作。

（1）建立了铆接有限元模型，并与基于体积不变假设的理论模型进行对比，验证了有限元模型的有效性。

（2）从理论上分析了铆接过程变形，根据铆钉变形特点和材料的弹塑性流动，将铆接过程划分为6个阶段，并对各个阶段进行受力和变形分析。

（3）分析了铆接力对钉孔径向变形的影响，表明铆接力越大，钉孔变形越大，但孔在被连接件厚度方向的变形极不均匀，且变形区域限于钉孔附近区域。

（4）分析了不同铆接力作用下，被连接件接合面上的应力应变状态，表明铆接力能够有效改变连接结构的寿命，但其影响的区域仅限于距孔边6R以内。

[1]王云渤,张关康,冯宗律,等.飞机装配工艺学[M].北京：国防工业出版社，1984.

WANG Yunbo, ZHANG Guankang, FENG Zonglü, et al.Aircraft assembly technology[M].Beijing: National Defence Industry Press,1984.

[2]CHERAGHI S H .Effect of variations in the riveting process on the quality of riveted joints[J].International Journal of Advanced Manufacturing Technology, 2008,39:1144-1155.

[3]MULLER R P G.An experimental and analytical investigation on the fatigue behaviour of fuselage riveted lap joints[D].Delft: Delft University of Technology, 1995.

[4]AMAN F, CHERAGHI H S, KRISHNA K, et al.Study of the impact of riveting sequence, rivet pitch, and gap between sheets on the quality of riveted lap joints using finite element method[J].International Journal of Advanced Manufacturing Technology, 2013,67:545-562.

[5]BLANCHOT V, DAIDIE A.Riveted assembly modelling: study and numerical characterisation of a riveting process[J].Journal of Materials Processing Technology, 2006, 180(1-3):201-209.

[6]MDERIJCK J J , HOMAN J J, SCHIJVE J, et al.The driven rivet head dimensions as an indication of the fatigue performance of aircraft lap joints[J].International Journal of Fatigue, 2007, 29(12):2208–2218.

[7]CALVIN R, STRAZNICKY P V, ALDERLIESTEN R.Riveting process induced residual stresses around solid rivets in mechanical joints[J].Journal of Aircraft,2007,44(1):323-329.

[8]ZHANG K F, CHENG H, LI Y.Riveting process modeling and simulating for deformation analysis of aircraft’s thin-walled sheet-metal parts[J].Chinese Journal of Aeronautics,2011,24:369-377.

[9]刘平，李原，张开富，等.压铆过程阶段划分与压铆力计算[J].机械科学与技术，2009，28(4):514-521

LIU Ping, LI Yuan, ZHANG Kaifu, et al.Stage division and upsetting force calculation for pressing rivet connection[J].Mechanical Science and Technology for Aerospace Engineering，2009,28(4):514-521

[10]王宇波，余路，洪华舟，等.自动钻铆连接件疲劳性能分析[J].南京航空航天大学学报，2012，44(21)：52-55.

WANG Yubo, YU Lu，HONG Huazhou, et al.Fatigue analysis of components produced by automatic drilling and riveting[J].Journal of Nanjing University of Aeronautics and Astronautics,2012,44(21):52-55.

[11]张岐良，曹增强，秦龙刚，等.钛合金电磁铆接数值模拟[J].稀有金属材料与工程，2013，42(9)：1832-1837.

ZHANG Qiliang, CAO Zengqiang, QIN Longgang, et al.Numerical simulation of electromagnetic riveting for titanium alloy[J].Rare Metal Materials and Engineering, 2013,42(9) :1832-1837.

[12]郭鸯鸯.电磁铆接铆钉变形及铆模结构优化的研究[D].哈尔滨：哈尔滨工业大学，2013.

GUO Yangyang.Research of rivet deformation and structural optimization of riveting die with electromagnetic riveting[D].Harbin: Harbin Institute of Technology,2013.

[13]SZOLWINSKI M P, FARRIS T N.Linking riveting process parameters to the fatigue performance of riveted aircraft structures[J].Journal of Aircraft,2000,37(1): 130-137.