某型飞机副翼作动系统静刚度与自然频率设计研究

李元元，任 磊，王培文

（1.中航工业第一飞机设计研究院，西安 710089；2. 中航工业西安飞机工业（集团）公司，西安 710089；3. 中航飞机西安研发中心，西安 710089）

民机采用全球招标形式，系统方面有大量供应商参与，一旦JDP（Joint Define Phase）阶段确定了相关参数，后续如果调整较大，需支付供应商大量研制经费。这就意味着在前期设计中就作动器本身参数、安装形式、外观尺寸要尽可能准确，一方面要减轻重量；另一方面要满足设计要求，使作动系统尽可能准确且最优化。基于该指导思想，在与供应商联合定义阶段以作动系统刚度与自然频率定量级关系（定性级原理性东西为一般工程人员常识，但定量计算国内工程上极少，这方面在高校理论研究较多但缺乏工程应用，国外的先进之处就是能够将理论与工程实践相结合，给出严格的定量级参数）为设计目标，结合外方其他机型经验共同开展多次迭代计算，尽可能准确计算出安装几何图、刚度与自然频率的关系。

通常情况下，由结构强度专业动强度组给出飞机舵面最小自然频率要求。飞控系统专业与供应商根据最小自然频率要求，设计作动器刚度、后梁位置安装刚度、舵面安装刚度。

1 副翼舵面作动器安装

1.1 商用飞机副翼舵面作动器常用安装形式

飞机刚度与作动器几何安装形式有着密切关系，下面列出了几种典型的大中型飞机舵面安装形式。

（1）法兰式安装（Flange-Mount Installation）曲柄滑块机构如图1所示。优点：左、右机翼可互换安装；液压与电气连接不需要考虑成活动连接；在铰链与大梁之间的活动距离由于有了中间连杆的作用，运动距离大大缩短。缺点：中间连杆需要根据铰链的活动，考虑活动范围，连接强度以及运动分析（有没有运动死点，急回特性等）；在大梁上需要开孔，活塞上具有侧向载荷，因此需要增加活塞杆的弯曲刚度。

（2）点-点式安装（Pin-Pin Installation）摇块机构，如图2所示。优点：相对于法兰安装式，不要求在后梁上开孔；在做动器上没有侧向载荷；便于安装与设计。缺点：在后梁与铰链之间有过大的距离；后梁与铰链连接点需要有足够的刚度与强度；一般情况下，左右机翼作动器不能互换；整个作动筒由于运动，要求液压管路，电气连接件需要考虑成可活动部件。

（3）应力连杆式安装（Reaction Link Installation），即一个自由度为0的三个杆机构+摇块机构，如图3所示。优点：整个机构刚度好；整个机构运动行程短，可以安装在大梁后部。缺点：作动器跟随着活塞的运动而摆动，因此液压管路与电气连接接口考虑活动连接；左右作动器不能互换安装；相对法兰式安装重量相对较大。主要用于干线飞机上，某在研干线客机部分主舵面采用此种安装方式。

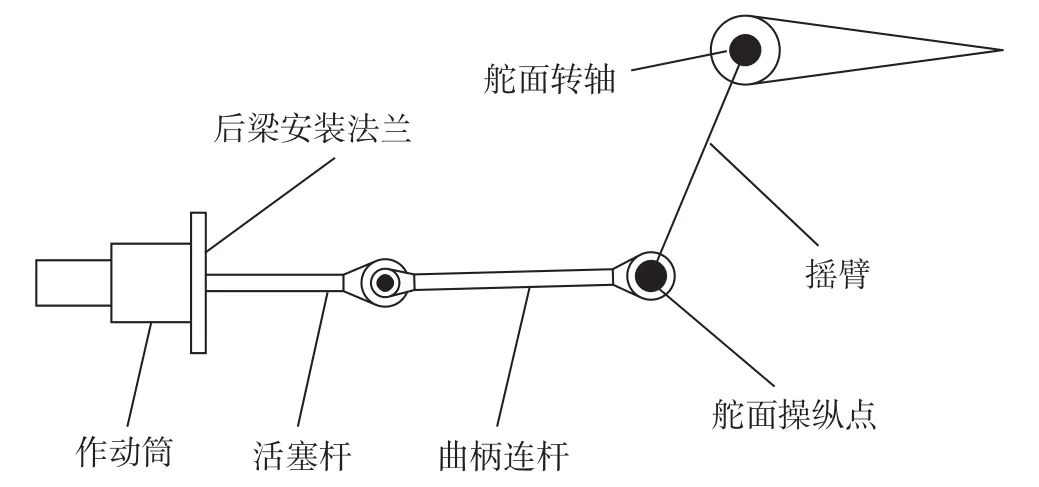
图1 飞机副翼舵面法兰式安装Fig.1 Flange-mount Installation for aileron surface

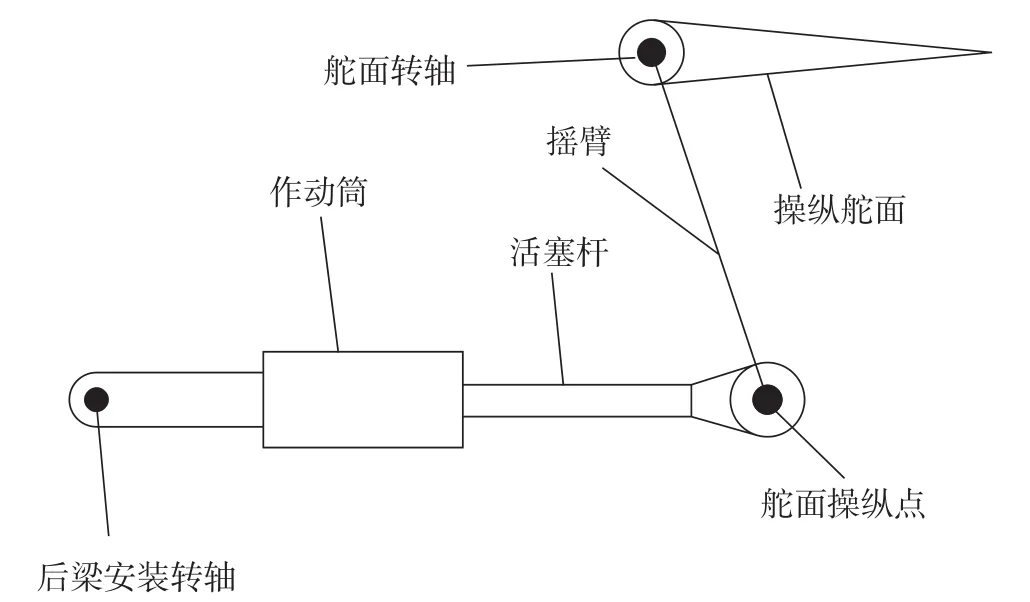
图2 点-点式安装Fig.2 Pin-pin installation

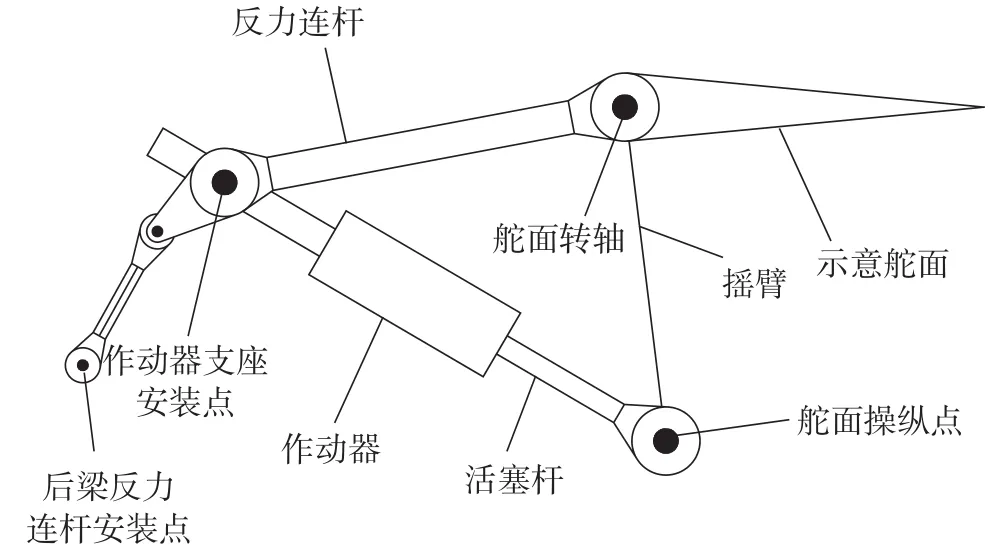
图3 应力连杆式安装Fig.3 Reaction link installation

1.2 某型机副翼舵面作动器运动参数

经过多次与供应商、结构设计部门、总体气动部门沟通计算，确定副翼舵面采用法兰式安装；运动饺点见图1。舵面偏角与有效力臂之间的关系如图4（a）所示；作动器行程与舵面偏角之间的关系如图4（b）所示；曲柄连杆和活塞杆之间夹角与舵面偏角关系如图 4（c）所示。可以看出曲柄连杆与活塞杆夹角变化非常小，在-1.4802°～1.1563°之间，可近似认为垂直；这种设计可减少作动器运动过程中的侧向力，避免法兰连接漏油问题。

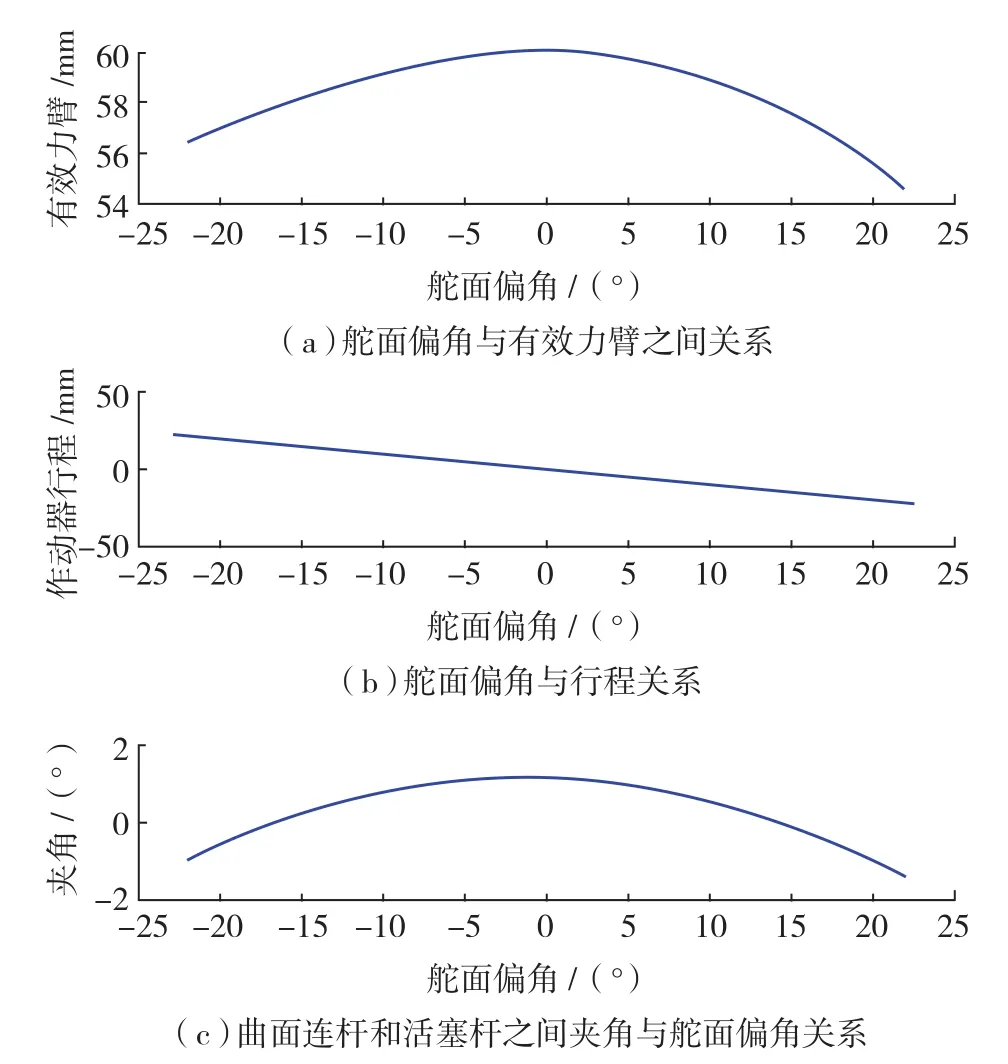
图4 法兰安装相关运动参数Fig.4 Kinmatics parameters of flange-mout installation

2 作动系统设计要求及设计参数

2.1 主机所提供的参数

（1）设计要求：总体颤振专业分下来的副翼舵面最小自然频率（饶转轴线）为一个作动器主动；另一个作动器脱开状态：30Hz。

（2）机体设计参数：舵面转动惯量J=1.007kg·m2；后梁安装基体刚度kr=2.851×107N/m； 看作一个与摇臂及安装有关的常值弹簧kl=4.81×107N/m，kl_r=4.81×107×0.060N·m/rad。

2.2 国外供应商PCU设计参数

PCU[1]：PCU内径=0.053m；活塞杆直径=0.032m；PCU伸出行程=0.0217m；PCU收回行程=0.0217m；作动筒有效面积=0.0014m2；左右腔行程余量=0.003m；伸出时作动筒的体积=3.4580×10-5m3；收回时作动筒体积=3.4580×10-5m3；有效杨式弹性模型（体积）=8.27×108Pa/m2；曲柄连杆刚度=7.74×107N/m；PCU轴向刚度=3.15×108N/m；PCU弯曲刚度变化非常小，可用下面公式计算：

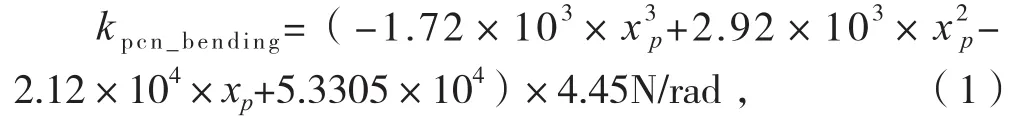
式中，xp是活塞杆相对于中立位置位移量， 计算结果如图5（e），可以看出作动器弯曲刚度变化极小，因此这里取常值kpcn_bending=2.372×105N/rad。

3 模型建立

该型飞机副翼舵面模型按照严酷工作状态，一个作动器工作状态，另一个作动器结构上脱开。建立计算模型如图6所示[1]。图6中，kr表示后梁基体刚度，单位N/m；kpcu_oil表示油液刚度，单位N/m；kpcu_bending表示活塞杆弯曲刚度，单位N/rad；kpcu_axial表示活塞杆刚度，单位N/m；kpcu_link表示曲柄连杆刚度，单位N/m；kl表示舵面操纵部位弯曲刚度（认为是一个常值旋转刚度，主要由舵面梁和舵面结构造成的），单位N/rad；Bd表示作动筒阻尼，单位N/m·s；Bl表示舵面阻尼（舵面结构造成的，不考虑气动阻尼），单位 N/m·s。

JDP阶段，主机所责任是依据后梁安装基体刚度kr、舵面刚度kl、阻尼Bl；外方提供依据作动器刚度kpcu（即图6中出除kr、kl、Bl以外所有参数），计算出系统刚度，进而算出自然频率范围，判断是否满足颤振组提出的最小自然频率要求。如果不满足，则与供应商共同协调修改设计参数，直到满足设计要求[2-3]。

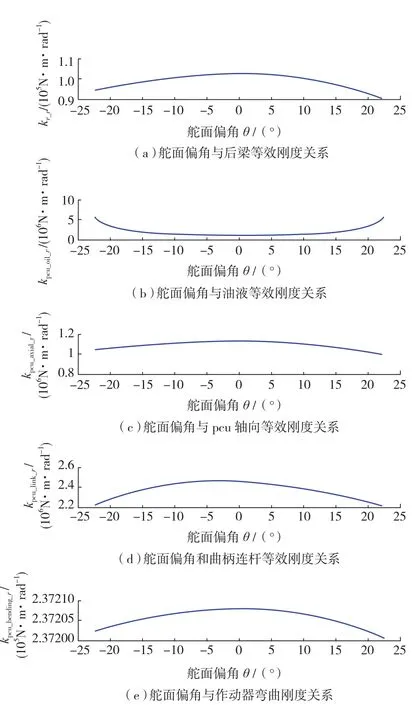
图5 机体刚度、油液刚度、作动器轴向刚度及曲柄连杆刚度折算刚度、作动器弯曲刚度Fig.5 Equivalent calculation for structure pad stiffness, oil stiffness, axial stiffness of actuator, rank-toggle link, and bending stiffness of actuator

图6 飞机副翼系统弹簧阻尼计算模型Fig.6 Spring and damp system model of aileron

4 刚度等效计算

4.1 系统等效刚度

通过如下公式计算[2-3]：

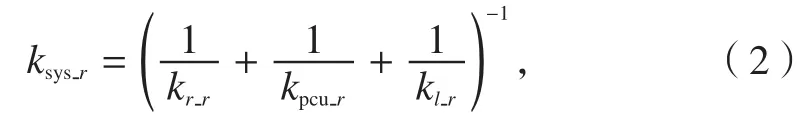
式中，ksys_r是作动系统等效旋转刚度，kr_r是机翼后梁上安装刚度kr等效到舵面上的旋转刚度，kpcu_r是作动器刚度kpcu等效到舵面上的旋转刚度，kl_r是舵面结构刚度kl换算到舵面的旋转刚度。各弹簧之间属于串联关系。计算出ksys_r之后，由得出自然频率fN范围[4]。

其中PCU刚度通过下式计算：

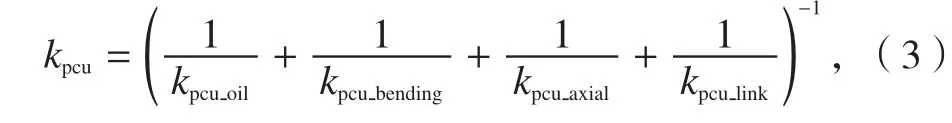
然后kpcu_r=kpcu(θ)，θ是舵面偏角。采用同样算法对作动系统刚度逐个等效计算，折算出总刚度。

4.2 等效刚度计算

4.2.1 活塞杆方向刚度等效

基体刚度kr等效计算：曲柄OB、连杆AB、初始角θ0、OD为已知量；舵面等效弹簧作用半径r，取r=OB。计算等效模型如图7所示。

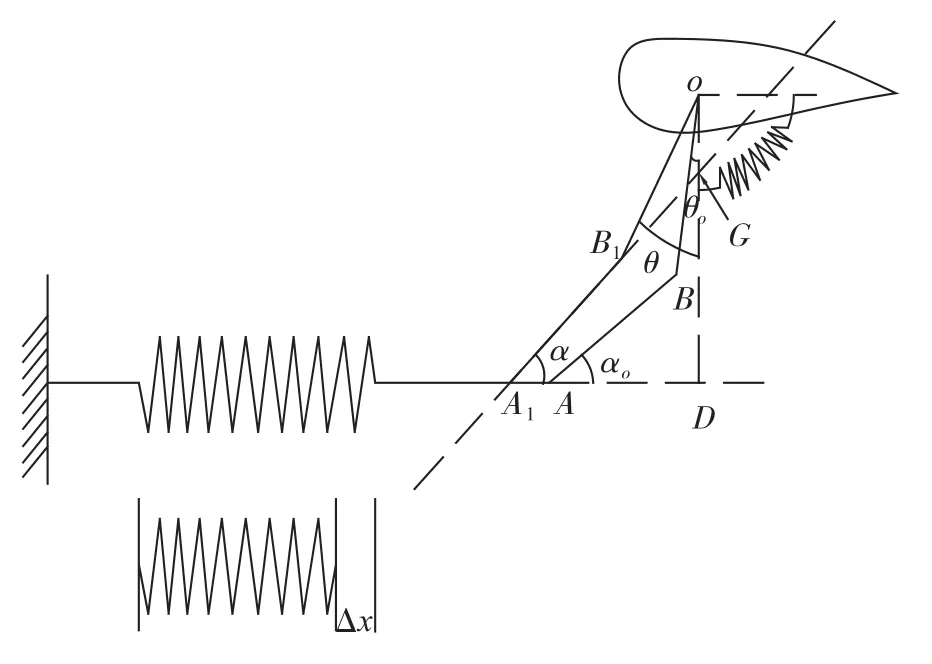
图7 活塞杆刚度等效计算Fig.7 Equivalent model for piston stiffness

位移角度之间的换量计算：推导公式kr_r=kr(θ)之间的关系。

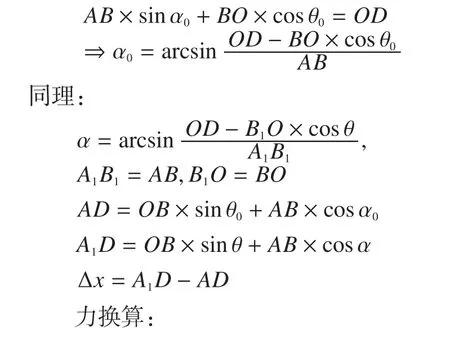
计算结果如图5（a）所示。其中油液刚度采用近似算法，由于油液刚度数量级相对于其他轴向刚度高一级，且法兰式运动交点图中曲柄连杆与活塞杆夹角极小，因此可近似按照垂直情况近似直接换算到舵面上，油液刚度计算公式[1]，油液刚度折算结果如图5（b）所示。作动器轴向折算结果如图5（c）所示。

4.2.2 曲柄连杆刚度等效计算

kpcu_link等效刚度计算：已知OB、AB（曲柄连杆初始长度）、OD、θ0，等效折算模型如图8所示。位移角度之间的换量计算：

曲柄连杆刚度等效计算结果如图5（d）所示。

4.2.3 作动器弯曲方向等效刚度计算

kpcu_bending等效刚度计算：弯曲刚度等效模型是一个四杆机构，已知OD、AD、AB、BC、CO，推导公式kpcu_bending_r=kpcu_bending(θ)之间的关系，等效算法与式（5）相同。如图9所示。

由于弯曲刚度方向上曲柄连杆与作动器活塞杆之间的夹角非常小，可以认为弯曲刚度是无限大；计算结果如图5（e）。为了便于计算，本文结合该机型法兰式安装几何尺寸，作动器弯曲刚度取其它类似飞机的试验测量最小值，折算刚度kpcu_bending_r=2.9596×107N·m/rad。

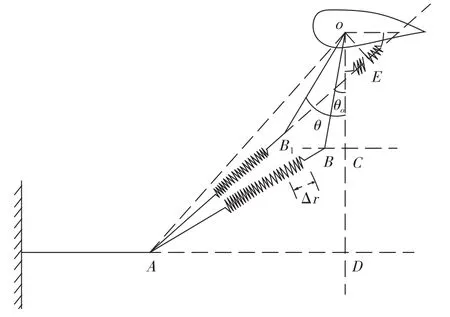
图8 kpcu_link曲柄连杆刚度等效计算Fig.8 kpcu_link equivalent stiffness of toggle link

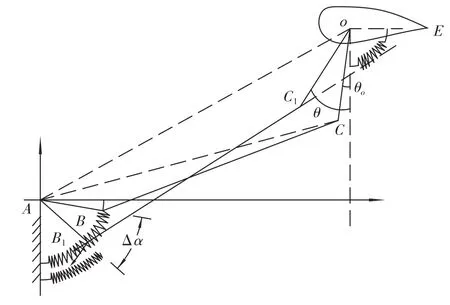
图9 kpcu_bending曲柄连杆刚度等效计算Fig.9 kpcu_bending equivalent stiffness of toggle link

5 系统总刚度及自然频率计算结果

计算出各等效刚度后，由公式：

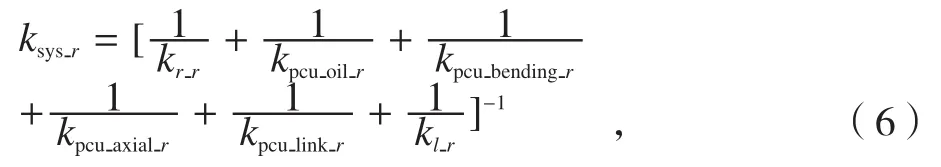
计算出上述等效刚度ksys_r之后，采用自然频率计算公式：给出系统自然频率与舵面偏角之间的关系，如图10所示。

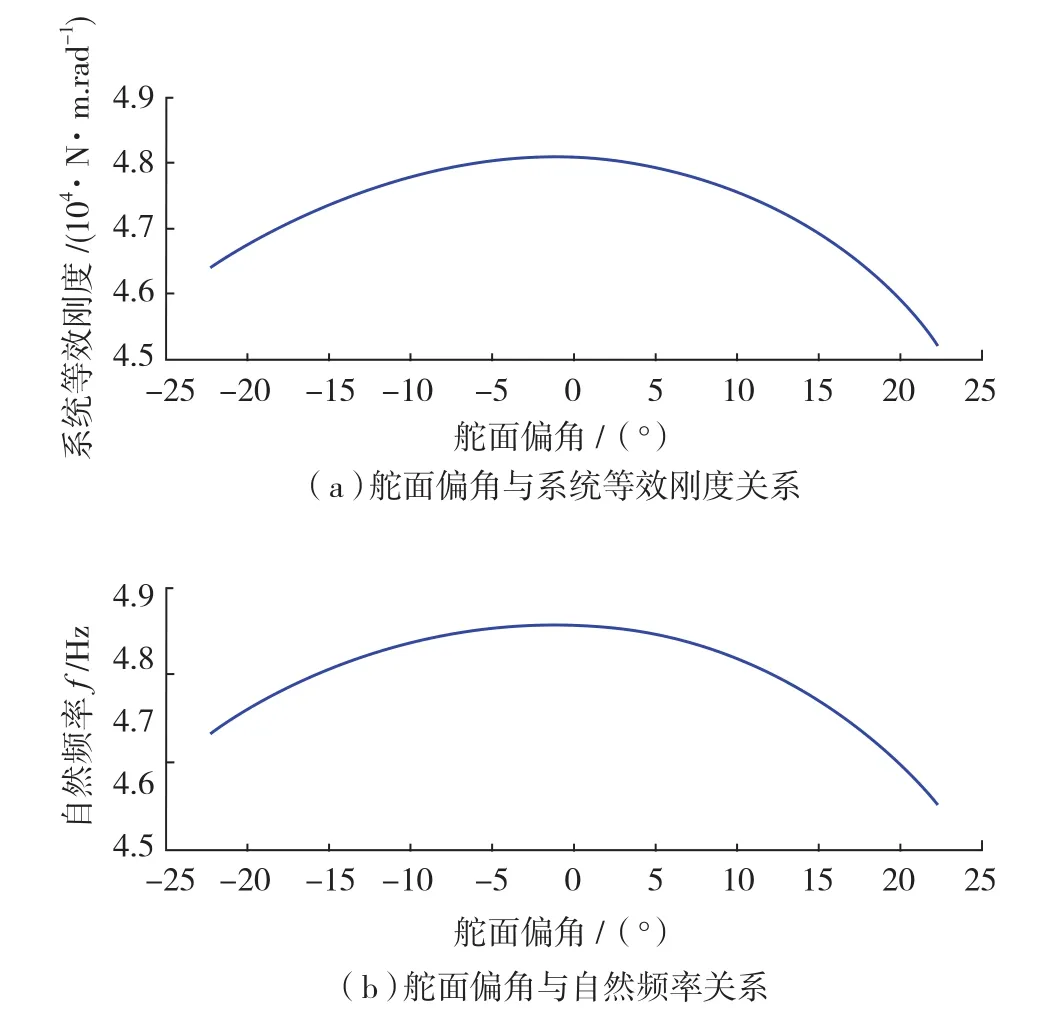
图10 系统整体刚度计算结果，作动系统设计自然频率与偏角关系Fig.10 System equivalent stiffness calculated results，relation ships between system stiffness and surface nature frequency

可以看出上述参数计算的系统自然频率为33.740～34.775Hz之间，满足总体设计最小自然频率要求。外方供应商根据主机所提供参数，并结合现役同类型飞机作动器参数，给出的试验测量结果（试验与定量计算同时进行），自然频率范围是33.1～34.8Hz，两者结果基本一致；证明该计算方法及结果是可以采纳的。

6 结束语

本文通过对舵面各刚度分析研究并将其折算到副翼舵面上，计算出了整个作动系统刚度，进而得出现有设计参数下作动系统自然频率，计算结果表明基本符合最小自然频率要求，并留有一定余量。该计算经过多次迭代核准，并与其他现役机型相比对。此外，与供应商试验结果基本一致。可以在后续合同中文件中要求供应商按照该参数设计作动器静刚度。以上主机所参数根据风洞试验结果、经验及强度设计给出；外方供应商参数来自现役同类型飞机，结果来自于供应商试验台架及定量计算。当然，整机设计单位后面还需在飞机铁鸟试验台架上对上述所有设计参数进行测试校对。另外，静刚度只是解决颤振问题一个方面，系统设计中还将与摘要中提到其他措施结合起来以获得良好的舵面颤振抑制功能。

本计算结果主要用作系统设计，供应商以此结果作为作动器静刚度设计依据。

[1]王占林.液压伺服控制[M].北京：北京航空航天大学出版社，1987.WANG Zhanlin. Hydraulic servo control[M]. Beijing： Beihang University Press, 1987.

[2]郭润江，霍应元.大型飞机操纵面颤振设计考虑[C].第十一届全国空气弹性学术交流会，昆明，2009.GUO Runjiang, HUO Yingyuan. Design consideration factor of larger aircraft control surface flutter[C]. The 11th national air elastic academic conferences, Kunming, 2009.

[3]王晓梅，沈磊.基于颤振抑制要求的舵面作动系统设计[J].高新技术企业，2011(20): 66-67.WANG Xiaomei，SHEN lei. Surface actuation system design based on flutter suppression requirement[J]. High and New Technology Enterprise,2011(20): 66-67.

[4]陈康宁，王磬，李天右，等.机械控制工程基础[M].西安：西安交通大学出版社，1997.CHEN Kangning, WANG Qing, LI Tianyou, et al. Mechanical control engineering[M]. Xi’an: Xi’an Jiaotong University Press,1997.