螺旋槽数控立铣刀圆周刃前角的测量及计算方法
2016-05-30唐臣升张滨义
王 巍,唐臣升,刘 健,张滨义,李 研
(1. 空军驻沈阳地区代表局,沈阳 110000;2.中航工业沈阳飞机工业(集团)有限公司,沈阳 110000)
随着数控机床尤其是数控铣床的普及,数控立铣刀的应用也越来越广泛、需求量也越来越大,大多数数控立铣刀的结构为螺旋槽数控立铣刀。钛合金、高温合金、超强度钢等典型难加工材料的应用[1],尤其是钛合金因其强重比高和防腐蚀优点被广泛用作航空航天飞行器材料[2],这些材料的加工对数控立铣刀切削性能的要求也就越来越高,而刀具的切削性能除了刀具材料外,主要与刀具的结构参数有关,其中最主要的结构参数是数控立铣刀螺旋切削刃的前角,螺旋切削刃的前角直接影响刀具的切削性能及其寿命[3]。由于螺旋切削刃的前刀面为螺旋曲面无法准确测量,只能间接、近似地测量,因此不能准确反应数控立铣刀实际的切削性能,不利于数控立铣刀的技术研究与应用,进而也影响了钛合金、高温合金、超强度钢等典型难加工材料的加工效率和精度。此外,在切削加工过程中刀具的前角和后角应该是实际作用前角和后角,而不是设计前角和后角。因此准确计算出数控立铣刀实际作用切削角度十分重要[4]。
本文阐述了一种螺旋槽数控立铣刀圆周刃前角测量方法和一种参数化数控立铣刀实际作用切削角度计算方法,实现了螺旋槽数控立铣刀圆周刃前角及其实际作用切削角度的精确测量与计算。
1 螺旋槽数控立铣刀圆周刃前角测量及计算方法
1.1 前角定义
螺旋槽数控立铣刀结构有多种,其中最为常用的是直柄螺旋槽数控立铣刀。本文就以种直柄螺旋槽数控立铣刀为例对螺旋槽数控立铣刀圆周刃前角测量及计算方法进行阐述。
图1为一种直柄螺旋槽数控立铣刀的主视图,图2是图1中沿A—A线剖面图,图3是图2中刃口部分的局部放大图。
图1中的1为螺旋槽数控立铣刀的刃部,2为柄部,3为螺旋槽的螺旋角。
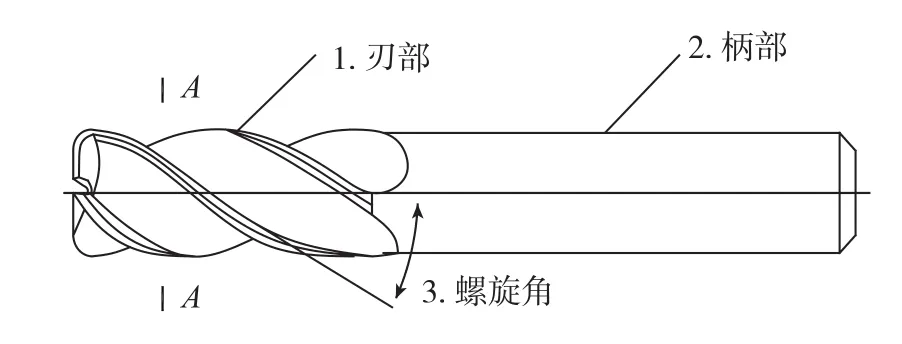
图1 一种直柄螺旋槽数控立铣刀的主视图Fig.1 Main view of the helical flutes CNC end-milling cutter with shank
图2中的4为螺旋槽数控立铣刀圆周刃前角,5为前角在前刀面上的测量长度,6为螺旋刃角度测量静止参考系中的基面与A—A剖面的交线,7为螺旋刃角度测量静止参考系中的切削平面与A—A剖面的交线。
图3中的8为前角在前刀面上的准确测量长度,9为前角在前刀面上的实际测量长度,10为前角在前刀面上的准确测量长度在基面上的投影长度,11为前角在前刀面上的实际测量长度在基面上的投影长度,12为刀具实际测量出的前角,13为刀具准确前角4与其实际测量值12的差值,14为刀尖处的圆弧半径,15为传统的前角测量误差[5]。
1.2 测量及计算方法
螺旋槽数控立铣刀圆周刃前角测量及计算方法分以下几个步骤:
(1)前角在前刀面上的准确测量长度d计算:将实际测得的前角在前刀面上的测量长度9(d')减去1个刀尖处的圆弧半径14(r),该值即为前角在前刀面上相对最为准确的测量长度8,亦即d=d'-r;
(2)前角的准确测量长度在基面上的投影长度l计算:将前角在前刀面上的实际测量长度在基面上的投影长度11(l')减去1个刀尖处的圆弧半径14(r),再减去以前角在前刀面上相对最为准确的测量长度8为斜边,以前角在前刀面上的实际测量长度在基面上的投影长度11(l')减去1个刀尖处的圆弧半径14(r)的差为邻边的夹角的正弦值与尖出的圆弧半径14(r)的积即为前角在前刀面上相对最为准确的测量长度在基面上的投影长度10(l),亦即

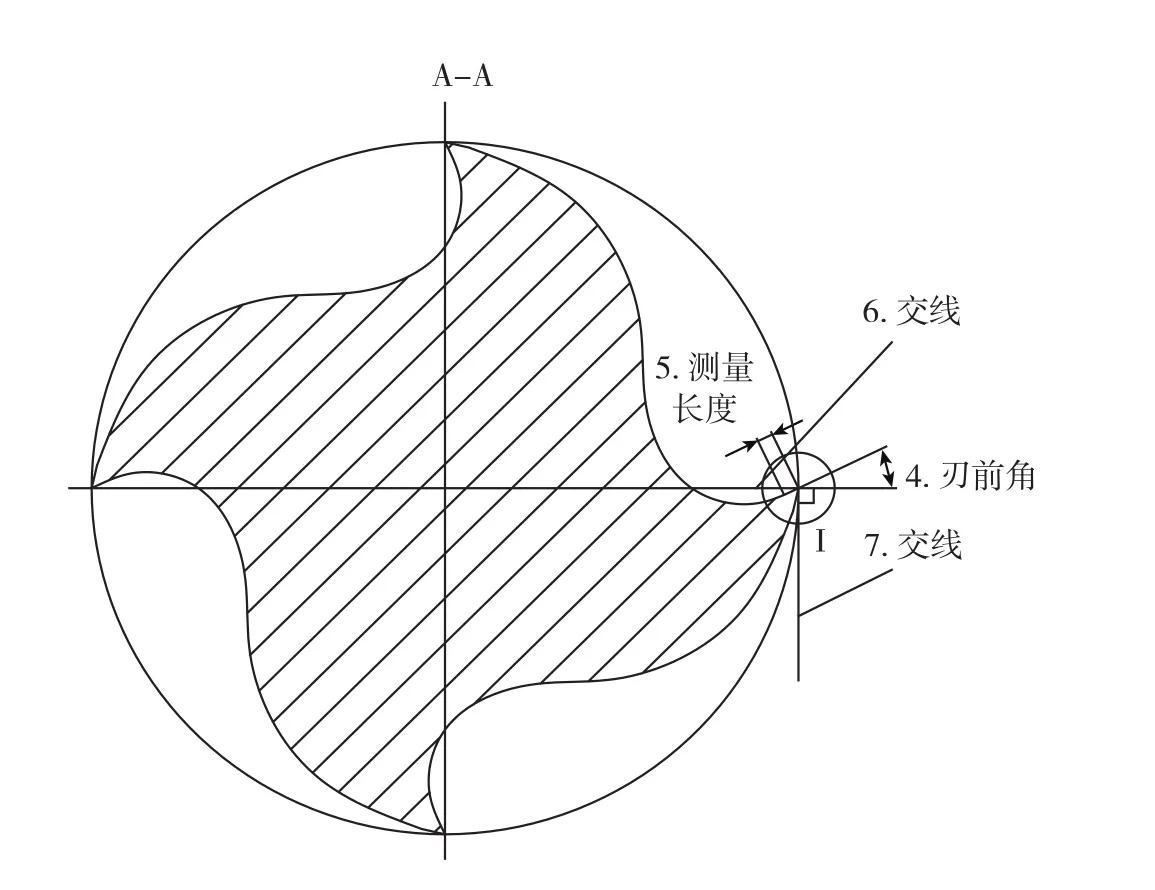
图2 一种直柄螺旋槽数控立铣刀的刃部横向剖视图Fig.2 Sectional view on the cutting section of the helical flutes CNC end-milling cutter with shank

图3 刃部横向剖视图中刃口部分的局部放大图Fig.3 Local enlarge figure of the edge in the sectional view on the cutting section
(3)螺旋槽数控立铣刀圆周刃的前角γ:根据上述的计算结果可以得出螺旋槽数控立铣刀圆周刃的准确前角4(γ)为以前角在前刀面上的准确测量长度8(d)为斜边,以前角的准确测量长度在基面上的投影长度l为邻边的夹角,亦即
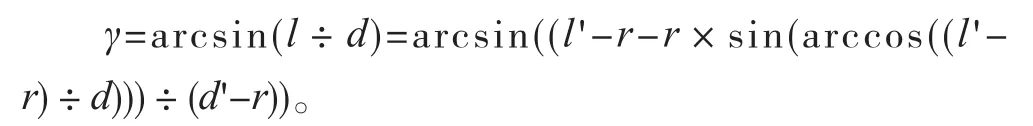
1.3 测量及计算方法的优点
该螺旋槽数控立铣刀圆周刃前角测量及计算方法的优点,应用以前的计算方法是以前角在前刀面上的实际测量长度为斜边与前角在前刀面上的实际测量长度在基面上的投影长度为邻边的夹角,亦即arccos(l1÷d1),由于没有考虑刀尖半径r的影响,因此测量误差较大。而应用该方法可以将螺旋槽数控立铣刀圆周刃前角测量误差明显小于原有测量方法的结果,尤其是前角的绝对值接近0°的时候,更好的满足数控立铣刀制造与应用技术的需要。
1.4 应用验证
该应用验证的实施例是测量一把直径为20mm、螺旋角为40°、螺旋切削刃前角为10°、前角理论测量长度为0.6mm、刀尖处的圆弧半径为0.05mm的4刃螺旋槽数控立铣刀。实际测得螺旋刃前角在前刀面上的长度为0.608mm,实际测得螺旋刃前角在前刀面上的长度在基面上的投影长度为0.605mm,依据该螺旋槽数控立铣刀圆周刃前角测量及计算方法得出该刀具螺旋刃前角的测量值为9.82°,误差值仅为0.18°,而应用以前的计算方法是以前角在前刀面上的实际测量长度为斜边与前角在前刀面上的实际测量长度在基面上的投影长度为邻边的夹角,亦即arccos(l1÷d1),则得出该刀具螺旋刃前角的测量值为5.69°,误差值为4.31°。由该实施例的测量结果可见,本螺旋槽数控立铣刀圆周刃前角测量及计算方法的测量远远小于以前的测量误差,其误差值如图3所示。
2 参数化螺旋槽数控立铣刀圆周刃实际作用切削角度的定义及计算方法
本文中的螺旋槽数控立铣刀圆周刃切削角度主要是指前角和后角。螺旋槽数控立铣刀圆周刃切削角度又分为设计(或静态)角度和动态角度,而螺旋槽数控立铣刀圆周刃实际作用切削角度就是动态角度。
2.1 静态切削角度的定义
对于螺旋槽数控立铣刀来说,其圆周刃静态切削角度的参考系主要由经过切削刃上选定点的基面和切削平面组成。
其中,基面就是经过切削刃上选定点并与刀具轴线重合的平面,而切削平面就是经过切削刃上选定点并与基面垂直的平面。
在静态参考系中,螺旋槽数控立铣刀圆周刃的静态前角为切削刃前刀面与基面的夹角,而静态后角为切削刃后刀面与切削平面的夹角[6]。
2.2 动态切削角度的定义
切削速度与进给速度使静态切削角度的参考系发生了变化,进而形成了新的参考系,即动态参考系。
在动态参考系中,螺旋槽数控立铣刀圆周刃的动态前角则为切削刃前刀面与基面的夹角,而动态后角为切削刃后刀面与切削平面的夹角[7]。
2.3 刀具实际作用切削角度计算的总体思路及计算方法
2.3.1 总体思路
刀具实际作用切削角度计算的总体思路如图4所示[8]。
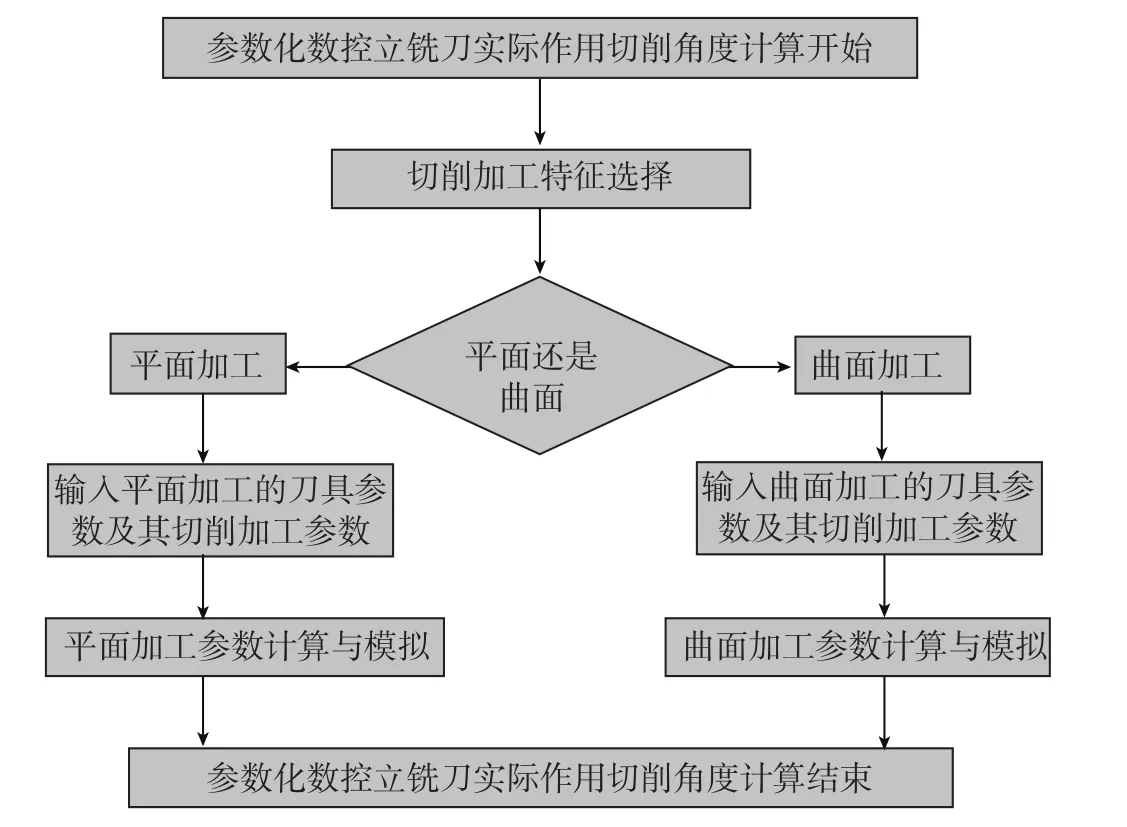
图4 刀具实际作用切削角度计算方法的总体流程图Fig.4 Total flow chart of calculating method on the effective cutting angle
2.3.2 计算方法
本文介绍的刀具实际作用切削角度计算方法是通过软件实现的,其设计思想是:刀具数控加工编程人员只要通过计算机界面从键盘输入刀具及其切削加工参数,计算机将自动计算出数控立铣刀实际作用切削角度并自动完成单齿切削厚度、最大作用前角、最小作用后角、单齿切削厚度、最大作用前角、最小作用后角等相关参数的计算。
本文介绍的刀具实际作用切削角度计算方法通过以下技术方案实现:
(1)参数化数控立铣刀实际作用切削角度计算开始。
(2)选择加工特征:平面加工或曲面加工。
(3)输入刀具参数及其切削加工参数:
·刀具直径
·切削刃数量
·刀具设计前角
·刀具设计后角
·刀具转速
·进给速度
·径向切削余量
·曲面的曲率半径
(4)参数计算。
根据刀具参数及其切削加工参数和相关信息完成参数计算与模拟。
主要计算参数有实际作用前角、实际作用后角、单齿切削厚度、最大作用前角、最小作用后角。具体计算方法如下:
①实际作用前角=设计(或静态)前角+前角变化量

其中,γ为实际作用前角,γ0为设计(或静态)前角,Δγ为前角变化量。
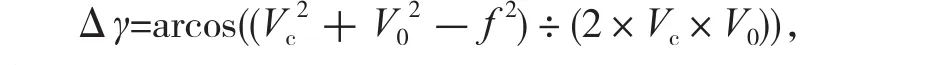
其中,Vc为切削的线速度,f为切削的进给速度,V0为Vc与f的合成进给速度。且

其中,r为刀具半径,d为刀具直径,n为刀具的转速,ae径向切削厚度。
②实际作用后角=设计(或静态)后角-后角变化量
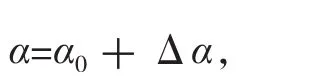
其中,α为实际作用后角,α0为设计(或静态)后角,Δα为后角变化量,而且,Δα=Δγ。
③单齿切削厚度:对于平面加工,单齿切削厚度t为:
单齿切削厚度=进给速度÷转速÷刀具齿数×cos(实际作用前角)
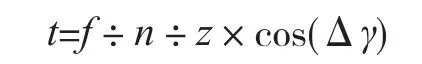
其中,z为刀具的齿数。
对于曲面加工,单齿切削厚度t为:
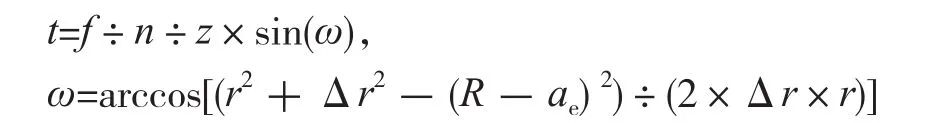
其中,r为曲面曲率半径,Δr为曲面曲率半径与刀具半径之差的绝对值。
④最大作用前角:最大作用前角就是当径向切削厚度等于刀具半径时的实际作用前角。
⑤最小作用后角:最小作用后角就是当径向切削厚度等于刀具半径时的实际作用后角。
(5)参数化数控立铣刀实际作用切削角度计算结束[9]。
2.3.3 计算方法的优点
参数化数控立铣刀实际作用切削角度计算方法可以准确计算出刀具实际作用前角、后角以及其他相关加工参数。应用该刀具实际作用切削角度计算方法只需10~15s就可计算出刀具实际作用前角、后角及其他相关加工参数。因此不仅提高了数控立铣刀实际作用切削角度计算效率,而且对提高数控切削加工质量和效率[10]以及数控切削加工的研究有极其重要意义。
3 结论
该螺旋槽数控立铣刀圆周刃前角测量及计算方法实现了螺旋槽数控立铣刀圆周刃前角的精确测量技术,而刀具实际作用切削角度的准确计算则能够更精确反映刀具的切削性能,从而更好的满足数控立铣刀制造与应用技术的需要。
[1]张昌娟,焦锋,赵波. 难加工材料精密切削技术研究[J]. 工具技术,2015(9):3-6.
ZHANG Changjuan, JIAO Feng, ZHAO Bo. Research of precision maching for difficult-to-machine material[J]. Tool Engineering,2015(9):3-6.
[2]杨学慧. 钛合金高效铣刀设计及性能研究[J]. 工具技术,2015(10):58-61.
YANG Xuehui. Design performance of titanium high efficiency cutter[J]. Tool Engineering, 2015(10):58-61.
[3]吴广东. TA15钛合金结构件高效铣削解决方案研究[J]. 工具技术,2015(1):58-60.
WU Guangdong. Solution research for titanium high efficiency endmilling [J]. Tool Engineering, 2015(1):58-60.
[4]刘杰华,任昭蓉. 金属切削与刀具使用技术[M].北京:国防工业出版社,2006:213-214.
LIU Jiehua, REN Shaorong. Technology for metal cutting and cutter application[M]. Beijing: Defence Industry Press, 2006:213-214.
[5]冯海峰,李吉,廖远洋. 一种小型化定精度计量结构的设计方法及工程实现[C]//第五届中国航空学会青年科技论坛文集.北京:北京航空航天大学出版社,2012:710-713.
FENG Haifeng. LI Ji, LIAO Yuanyang. Design method for fixed accuracy of small metering structure and engineering application[C]//5th CSAA science and technique youth forum. Beijing: Beijing Aeronautic and Astronautic University Press, 2012:710-713.
[6]太原市金属切削刀具协会编. 金属切削实用刀具技术[M].北京:机械工业出版社, 2006.
Taiyuan Metal Cutting Association. Practical technology for metal cutting[M]. Beijing: China Machine Press, 2006.
[7]唐臣升,张滨义,杨巍,等. 数控立铣刀动态几何参数自动计算与模拟[J].航空制造技术,2014(1/2): 115-117.
TANG Chensheng, ZHANG Binyi, YANG Wei, et al. Automatic calculation and simulation for dynamic parameters of NC end-milling cutter[J]. Aeronautical Manufacturing Technology, 2014(1/2):115-117.
[8]张宏星,赵勇. CAD技术及系统研究概述[J]. 机械工程师,2004(7):7-9.
ZHANG Hongxing, ZHAO Yong. Systematic research for CAD technology[J]. Mechanical Engineering,2004(7):7-9.
[9]袁哲俊,刘华明. 刀具设计手册[M].北京:机械工业出版社,1999:402-403.
YUAN Zhejun, LIU Huaming. Cutter design manual[M]. Beijing:China Machine Press, 1999:402-403.
[10]杨双. 插铣加工技术的研究与应用[J]. 金属加工,2014(20):24-27.
YANG Shuang. Plunge milling technology research and application[J].Metal Working, 2014(20):24-27.
