复材C梁角度偏差对装配静强度影响的建模仿真研究*
2016-05-30
(上海交通大学上海市复杂薄板结构数字化制造重点实验室,上海 200240)
复合材料因具有强度高、刚度大、抗疲劳性强且重量轻的特点,在飞机制造领域得到越来越广泛应用[1]。复合材料C形梁作为升降舵、方向舵以及机翼翼盒等的重要组成,是飞机结构中常见的受力构件。
复合材料C形梁在制备过程中由于自身的材料性能、固化特性和温度等影响,导致在脱模过程中容易发生收缩回弹,致使C形梁的腹板与缘条的夹角角度不等于预设的角度,产生角度偏差。该制造过程中产生的角度偏差会对其装配过程及装配性能造成影响。
近年来,国内外对复合材料C形梁角度偏差的研究多集中在其成型机理以及影响因素上。岳广全等[2]从模具影响复合材料构件变形和残余应力的各种因素出发,分析了模具因素导致回弹变形造成的角度偏差。魏冉等[3]回顾了复合材料固化成型后回弹变形现象的产生及其影响因素,继而对回弹现象的模拟预测方法进行综述。Kappel等[4]则对引起脱模回弹现象的热膨胀因素和化学因素进行了量化。Svanbeg[5]等、Wucher等[6]通过建立有限元模型,在热影响的基础上提出了C形梁形状弯曲的不同也是产生夹角偏差的一个重要因素。
Fernlund[7]等的研究表明,固化过程中固化温度与环境温度之间的温度差是引起回弹变形的重要因素,且变形量正比为温度差。陈晓静[8]则采用有限元数值分析方法,提出了基于节点变形的型面补偿算法。贾丽杰等[9]以典型C形结构的缩比试验件入手,同时借助仿真模拟手段,预测C形结构回弹变形的拟合公式。上术研究对复合材料C形梁角度偏差的成因进行了阐述,但在实际生产中仍不可避免地会出现角度偏差。如图1所示的典型的复合材料升降舵结构,由复合材料C形梁与蒙皮以及金属接头装配而成。在复合材料C形梁的制造过程中由于回弹变形产生了回弹角,与接头装配的时候会产生装配干涉,影响装配,如图2所示。
目前,对角度偏差在一定范围内的复合材料C形梁,可通过施加外力使角度修正到理论位置再进行装配。然而该过程会导致装配结构含有初始应力,对装配结构的静载强度造成影响。
本文针对含有角度偏差的复合材料C形梁典型装配结构,建立一种研究其角度偏差对装配结构的静载强度影响的有限元模型,设计含有角度偏差的典型结构的单拉试验以获得最大静载强度的试验数据,并对有限元模型进行仿真模拟以及运算,与试验结果对比验证模型的有效性。
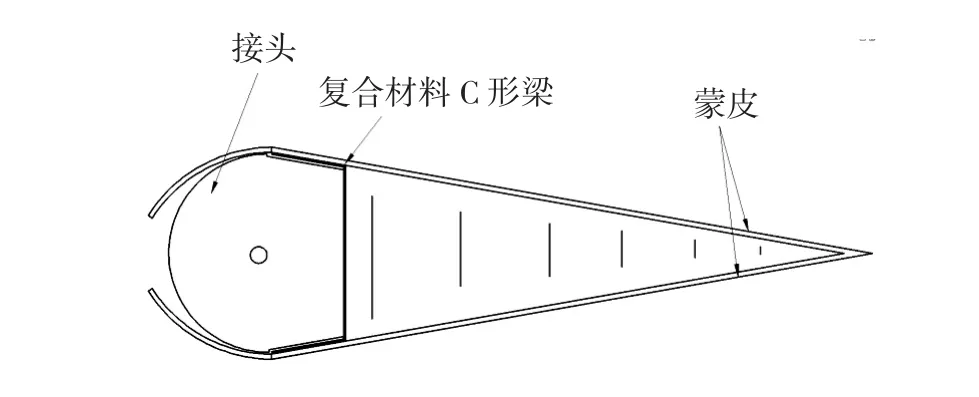
图1 升降舵结构示意图Fig.1 Elevator structure diagram
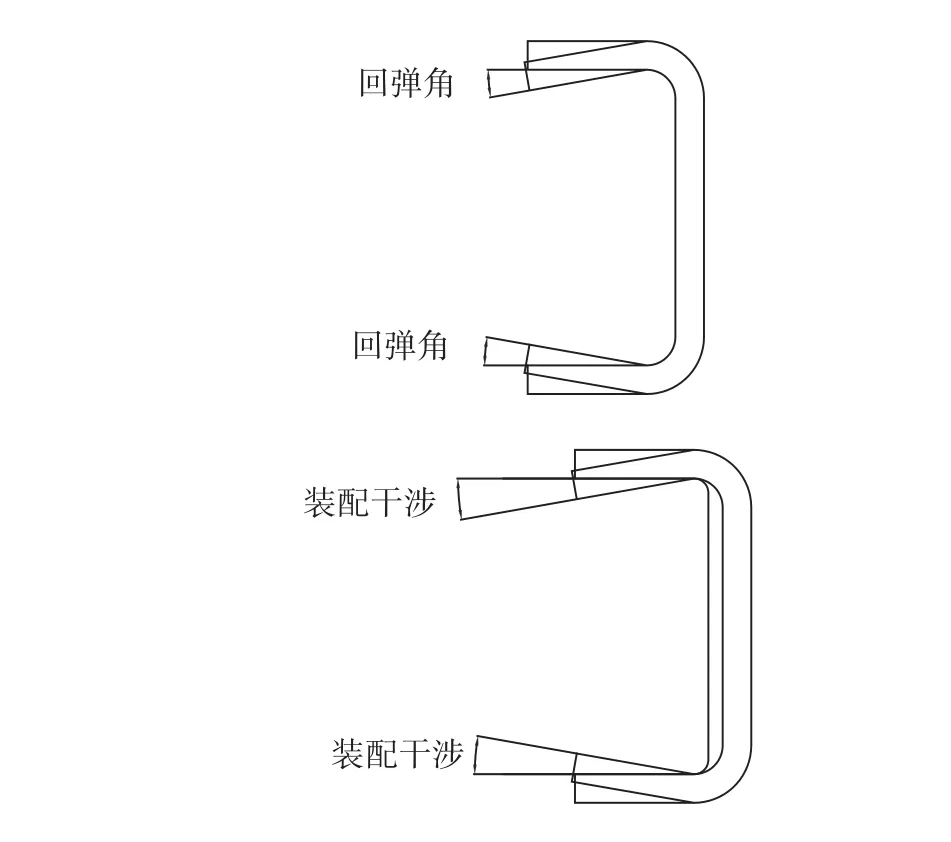
图2 角度偏差在升降舵装配中导致的干涉Fig.2 Interference caused by R-angle deviation in elevator assembly
1 复合材料C形梁试验件与测试
由升降舵的结构设计复合材料C形梁组成的典型装配结构,其中外侧为复合材料C形梁,内侧为配做段用来模拟实际结构中复合材料C形梁所连接的接头。试验所使用的复合材料C形梁角度为90°,通过设计制造不同角度的配做段,并将复合材料C形梁和配做段一同制孔后使用M6的螺栓螺接装配,模拟制造角度等于理论角度、制造角度大于理论角度以及制造角度小于理论角度的复合材料C形梁的典型装配结构。试验中选用的复合材料C形梁为T700碳纤维Epotech 3325A/B环氧树脂基复合材料,配做段为7075铝合金材料。复合材料C形梁长度为40mm,厚度为3.32mm,缘条与腹板夹角为90°。配做段长度也为40mm,厚度为2mm,缘条与腹板夹角分别为90°、86°和93°,具体尺寸如图3所示。
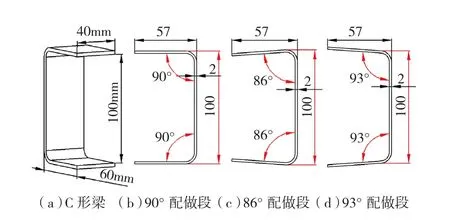
图3 试验件尺寸Fig.3 Size of specimens

图4 试验件Fig.4 Specimens

图5 试验件装夹Fig.5 Fixture of specimens
在螺接时,通过扭力扳手施加2N·m的预紧力以保证紧密连接。一共设计4个试验,试验1-1和试验1-2为重复试验,将复合材料C形梁与90°配做段装配,模拟实际生产的复合材料C形梁没有角度偏差的装配;试验2为复合材料C形梁与86°配做段装配,模拟实际生产的复合材料C形梁角度为90°,大于理论角度86°的装配;试验3为复合材料C形梁与93°配做段装配,模拟实际生产的复合材料C形梁角度为90°,小于理论角度93°的装配。试验件如图4所示。
测量试验件的角度值,其中试验1-1和1-2的试验件的角度为90°,试验2的试验件的角度为87.5°,试验3的试验件角度为91.5°。
将专用工装夹具安装于拉伸机上并夹持住试验件边缘,夹具下端固定,上端通过拉伸机按照4mm/min的速度对试验件进行拉载荷的施加,如图5所示。
2 有限元分析
根据复合材料C形梁的实际尺寸及铺层方式建立有限元模型。铺层方式为[+45/-45]7s共28层,铺层堆叠方向由C形梁内侧指向外侧。
将C形梁按照上、下翼缘,腹板,上、下夹角划分为5部分,分别按铺层堆叠方向扫略划分网格,将夹角区域网格密度增加以保证夹角区域的求解精度。同样根据配做段和螺栓、螺母的实际尺寸建立有限元模型,如图6所示。其中网格划分了22242个节点、14902个C3D8R单元。
根据螺栓预紧力公式:
预紧力矩Mt=K×P×d×0.001(N·m),
式中:K表示拧紧力系数,取K=0.2;d表示螺纹公称直径;求出预紧力P并在有限元模型中对螺栓施加预紧力。
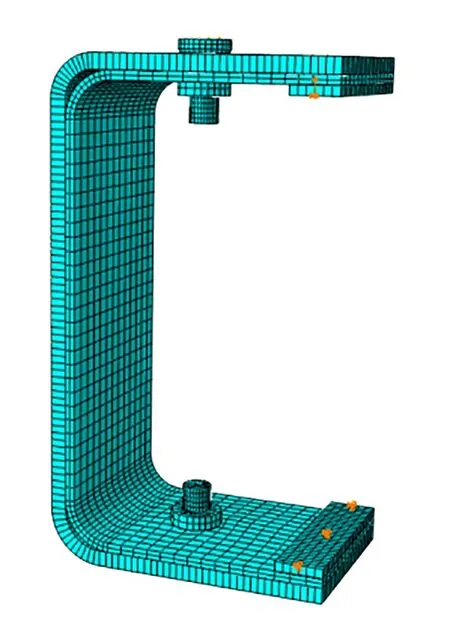
图6 有限元模型Fig.6 FEM model
设置刚体压片模拟施加载荷的工装夹具压片,将压片与配做段建立绑定(tie)约束,下侧压片固定,当拉伸试验件时对上侧压片施加拉向位移载荷。
对于试验1-1、1-2,直接对上侧压片施加的拉向位移载荷进行仿真即可。对于试验2和试验3需要增加对角度的修正仿真步骤。先对配做段施加位移载荷修正到90°,随后使复合材料C形梁与其螺接装配,施加螺栓预紧力。取消对配做段施加的位移载荷,使整个有限元模型自平衡,从而实现对试验件修正的仿真模拟。最后对上侧压片施加的拉向位移载荷进行仿真。
试验中选用的复合材料C形梁为T700碳纤维树脂基复合材料,具体材料参数如表1所示。配做段为7075铝合金材料,弹性模量71GPa,泊松比0.33。E1/E2分别表示X/Y方向的弹性模量,V12表示泊松比,G12表示剪切模量,XT/XC表示X方向的拉伸和压缩强度,YT/YC表示Y方向的拉伸和压缩强度。
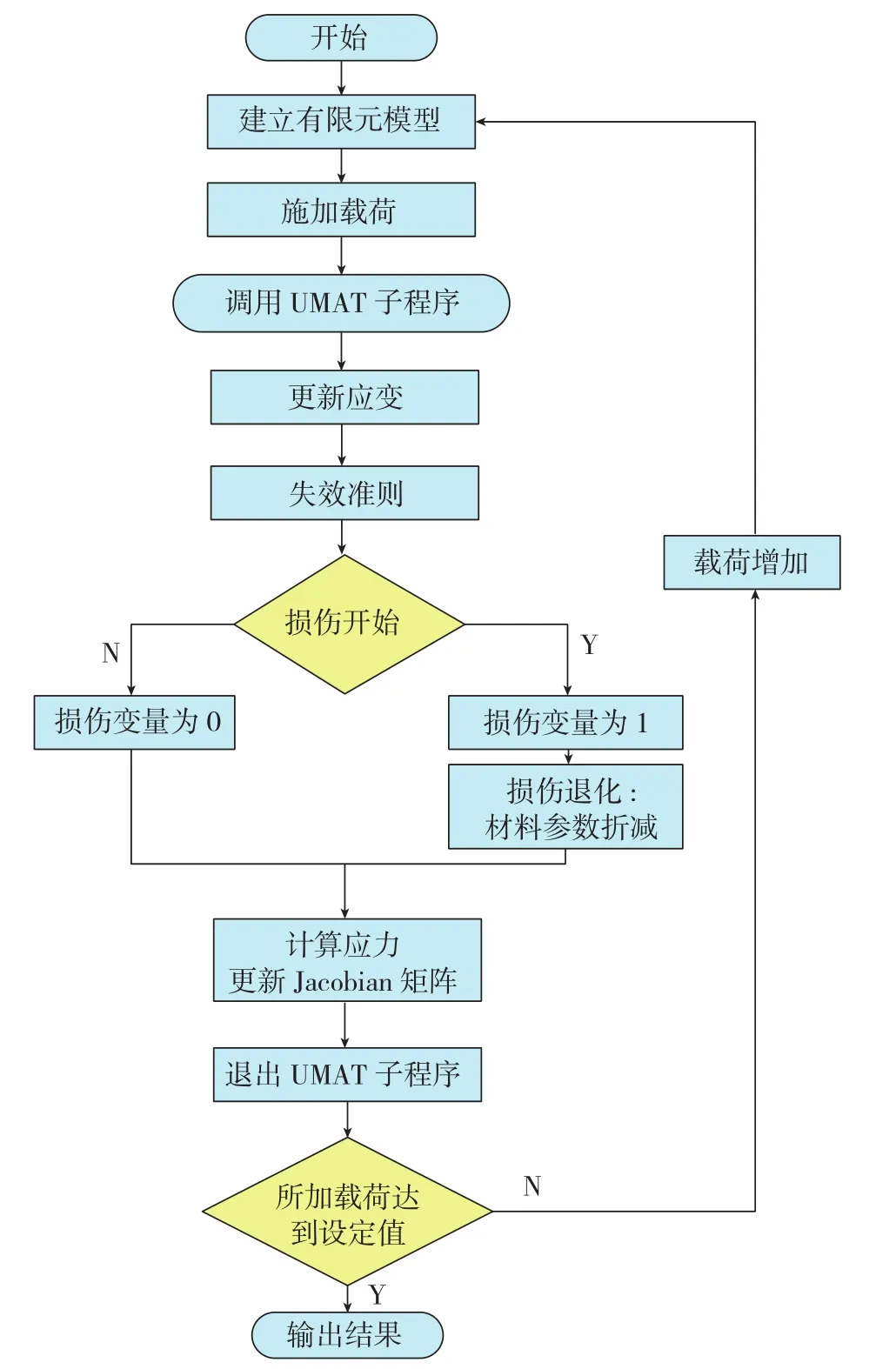
图7 UMAT仿真流程图Fig.7 Simulation flowchart of UMAT

表1 复合材料参数
基于ABAQUS有限元软件,建立上述有限元模型。在施加位移载荷过程中,会发生复合材料单元的失效。发生失效区域的应力分布变化剧烈,然而结构中的应变在失效前后变化比较平滑,更适合用来作为复合材料结构中损伤演化的判据[10]。三维Hashin准则[11]因区分了纤维断裂、基体开裂以及分层失效等不同的失效形式且简单准确的特点被广泛使用。因此本研究采用基于三维Hashin准则的应变形式[12]进行失效判定。
当单元应变满足失效准则时,根据具体失效形式对材料参数进行退化,对未发生失效的单元保持原有材料参数不变。对于发生多种失效模式的单元,材料参数的退化叠加。参考Kermanidis等[13]的损伤退化理论,对发生失效的单元根据失效形式进行材料参数的折减。
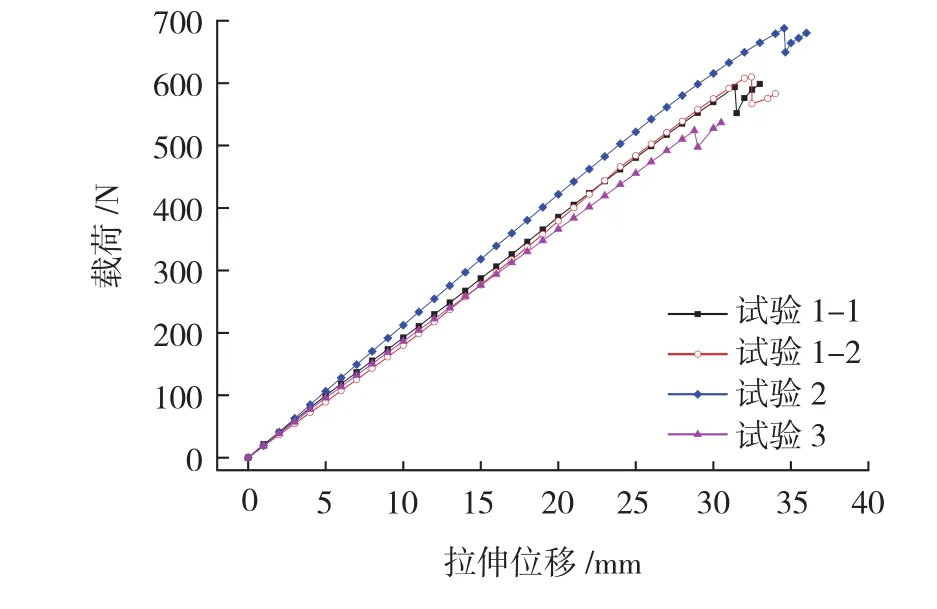
图8 载荷-位移曲线Fig.8 Load-displacement curves
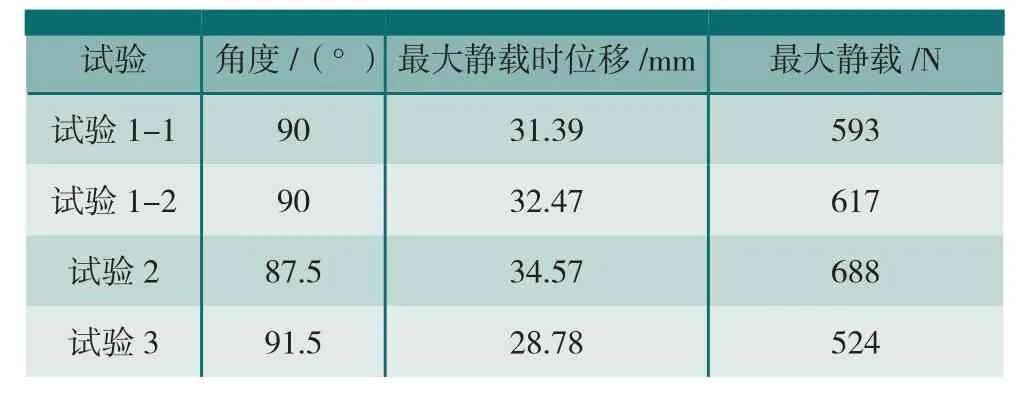
表2 试验静载强度
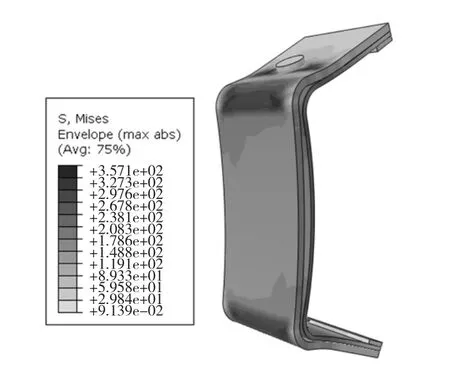
图9 试验1-1的仿真应力云图Fig.9 Simulation stress nephogram for TEST 1-1

图10 试验和仿真数据对比Fig.10 Comparisons of the experimental and simulation data
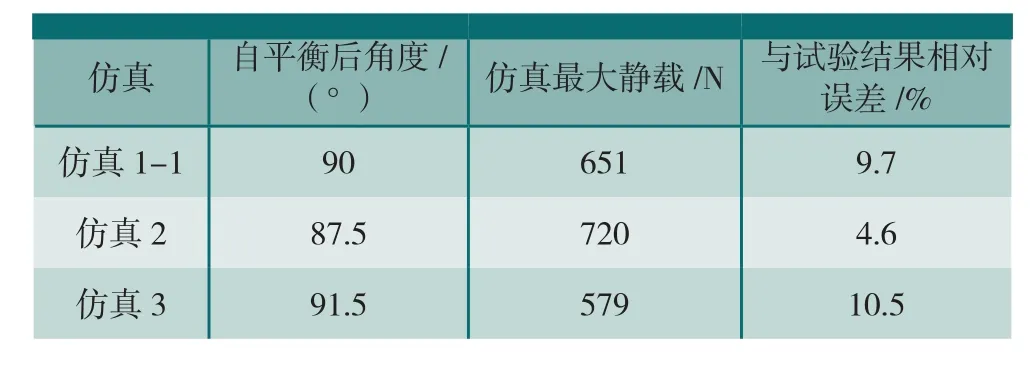
表3 试验和仿真结果对比
根据损伤模型中的失效形式及损伤退化使用FORTRAN语言编写用户材料子程序(UMAT),对复合材料C形梁的典型装配结构在拉伸过程中的损伤情况进行仿真,得到位移与载荷的关系曲线。UMAT子程序从ABAQUS主程序中调用初始材料参数、应变及应变增量,进行失效分析及损伤退化后向主程序提供应力,以及应力增量对应应变增量的变化率,即Jacobian矩阵。图7为使用UMAT进行仿真的流程图。
3 数据分析和对比验证
试验1-1、1-2、2和3的拉伸位移及载荷曲线如图8所示。在拉伸过程中,开始时复合材料C形梁和配做段一同承力,但是由于复合材料C形梁的刚度要强于配做段,因此复合材料C形梁起到主承力的作用。随着位移的增加,复合材料C形梁产生损伤,承载能力逐步下降,最后完全失效后由配做段承力。在该过程中,载荷曲线第一次下降时复合材料C形梁发生纤维断裂和分层等显著损伤,此时其典型装配结构发生失效,故将载荷曲线第一次下降时的载荷认为是该装配结构的静载强度。静载强度和拉伸位移如表2所示。
试验1-1和试验1-2为重复试验,都是90°的装配段进行拉伸试验,试验1-2的最大静载和试验1-1的最大静载偏差4%,因此可以认为试验具有较好的稳定性。
对上步建立的仿真模型进行仿真运算,试验1-1的仿真结果的应力云图如图9所示。
试验1-1、试验2和试验3的试验和仿真数据对比如图10和表3所示。
仿真自平衡后的角度与实际试验的角度偏差相同。仿真数据相对于试验数据整体偏大,但误差小于11%,与试验数据一致,准确性较高。因此本文建立的有限元模型是有效的。
4 结论
本文对含有角度偏差的复合材料C形梁的典型装配结构的静载强度进行研究,设计了含有角度偏差的典型结构的单拉试验以及建立了有限元模型。分别对含有制造角度等于理论角度、制造角度大于理论角度以及制造角度小于理论角度的复合材料C形梁的典型装配结构进行了试验和仿真模拟运算,将试验数据和仿真数据对比,验证了本文建立的有限元模型的有效性,为进一步分析复合材料C形梁的角度偏差对其典型装配结构的静载强度影响规律提供了理论基础。
[1]杜善义.先进复合材料与航空航天[J].复合材料学报,2007,24(1):1-12.
DU Shanyi. Advanced composite materials and aerospace engineering[J]. Acta Materiae Compositae Sinica, 2007, 24(1):1-12.
[2]岳广全,张博明,杜善义,等.模具对热固性树脂基复合材料固化变形的影响[J].玻璃钢/复合材料,2010(5):62-65.
YUE Guangquan, ZHANG Boming, DU Shanyi, et al. Influence of the mould on curing induced shape distortion for resin matrix thermosetting composites[J]. Fiber Reinforced Plastics/Composites, 2010(5):62-65.
[3]魏冉,贾丽杰,晏冬秀,等. 热固性复合材料结构固化回弹变形研究进展[J]. 航空制造技术, 2013(23):104-107,110.
WEI Ran, JIA Lijie, YAN Dongxiu, et al. Study progress of curinginduced spring back for thermosetting composites[J]. Aeronautical Manufacturing Technology, 2013(23):104-107,110.
[4]KAPPEL E, STEFANIAK D, HÜHNE C. About the spring-in phenomenon: quantifying the effects of thermal expansion and chemical shrinkage[M]//Adaptive, Tolerant and Efficient Composite Structures.Springer Berlin Heidelberg, 2013: 275-283.
[5]SVANBERG J M, ALTKVIST C, NYMAN T. Prediction of shape distortions for a curved composite C-spar[J]. Journal of Reinforced Plastics and Composites, 2005, 24(3):323-339.
[6]WUCHER B, LANI F, PARDOEN T, et al. Tooling geometry optimization for compensation of cure-induced distortions of a curved carbon/epoxy C-spar[J]. Composites Part A: Applied Science and Manufacturing, 2014, 56: 27-35.
[7]FERNLUND G,POURSARTIP A. The effect of tooling material,cure cycle,and tool surface finish on spring-in of autoclave processed curved composite parts[C]. The 12th International Conference on Composite Materials (ICCM12), Paris, 1999.
[8]陈晓静. 复合材料构件固化成型的变形预测与补偿[D]. 南京:南京航空航天大学,2011.
CHEN Xiaojing. Deformation prediction and compensation for composite components during curing process[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2011.
[9]贾丽杰,魏冉,杨霓虹,等. 复合材料C形结构的回弹变形研究[J]. 航空制造技术, 2013(23/24):121-124.
JIA Lijie, WEI Ran, YANG Nihong, et al. Study of spring-back for C-section composites part[J]. Aeronautical Manufacturing Technology,2013(23/24):121-124.
[10]张彦, 朱平, 来新民, 等. 低速冲击作用下碳纤维复合材料铺层板的损伤分析[J]. 复合材料学报,2006,23(2):150-157.
ZHANG Yan, ZHU Ping, LAI Xinmin, et al. Low-velocity impact damage analysis in carbon fiber reinforcedcomposite laminated plates[J].Acta Materiae Compositae Sinica,2006,23(2):150-157.
[11]HASHIN Z. Fatigue failure criteria for unidirectional fiber composites[R]. Pennsylvania: University Pennsylvania, 1980.
[12]WANG Y Q, TONG M B, ZHU S H. Three dimensional continuum damage mechanics model of progressive failure analysis in fibre-reinforced composite laminates[C]//Proceedings of 50th AIAA Structures, Structural Dynamics, and Materials Conference. California:American Institute of Aeronautics and Astronautics, 2009.
[13]KERMANIDIS T, LABEAS G, TSERPES K I, et al. Finite element modeling of damage accumulation in bolted composite joints under incremental tensile loading[C]//Proceedings of European Congress on Computational Method in Applied Sciences and Engineering, Barcelona,2000.
