采用Matlab的六自由度机器人三维运动学仿真

李庆, 谢一首， 郑力新， 张裕坤， 庄礼鸿

(华侨大学 工业智能化技术与系统福建省高校工程研究中心， 福建 泉州 362021)



采用Matlab的六自由度机器人三维运动学仿真

李庆, 谢一首， 郑力新， 张裕坤， 庄礼鸿

(华侨大学 工业智能化技术与系统福建省高校工程研究中心， 福建 泉州 362021)

摘要：对SA1400型六自由度工业机器人进行三维的运动学建模与仿真，建立机器人的正逆运动学方程，并得到正逆解.为验证方程及所求解的正确性，首先，使用Solidworks建立机器人各个部件三维模型；然后，用Matlab将所求得的正逆解编写为程序，导入机器人各部件，利用Matlab的三维绘图功能，以显示机器人的三维模型，并对机器人按轨迹运动的过程进行动态仿真，记录运动过程中机器人各关节角度值的变化，提示求解得到的不合理角度值和奇异点.结果表明：仿真过程较真实地模拟了实际机器人的运动情况，仿真结果达到预期目标，证明根据正逆运动学方程求得的解的准确性和可行性.

关键词：三维仿真； 工业机器人； 六自由度； 运动学； Matlab

机器人是“智能制造”这一主题下最受关注的领域之一.虽然中国已成为世界第一的机器人大国，但国产机器人的水平与国外相差较大，关键技术和零部件仍依赖进口，精度、稳定性和寿命不如国外生产的机器人，应用也主要集中于沿海地区的汽车和电子制造业.此外，我国机器人产业还存在“产、学、研”脱节的问题，机器人制造企业很难通过有效渠道获得与掌握研究机构及高校的最新成果.在机器人研究中，仿真是非常重要的环节，正确、合理的仿真可以减少实体机器人运行过程中的各种问题.本文采用Matlab对六自由度机器人进行三维运动学仿真.

(a) 结构图 (b) D-H坐标系　　图1　SA1400机器人Fig.1　SA1400 robot

1运动学建模

机器人运动学实现由机器人关节变量组成的关节空间与笛卡尔空间之间的相互转换.运动学的研究包含2个方面：一是正运动学，由机器人各关节角度计算机器人末端的位置与姿态；二是逆运动学，由末端的位置与姿态求解机器人在此位姿的各关节角度[1].SA1400型机器人的结构图与D-H坐标系，如图1所示.相邻连杆n-1与n之间的D-H坐标系变换矩阵[2-3]为

各连杆的D-H参数，如表1所示.表1中：θn为关节n的旋转角度，即两连杆夹角，符合右手定则为正；dn为关节n的偏距，即两连杆距离；αn为关节n和n-1轴线之间的夹角，即连杆扭角， 符合右手定则为正；an为关节n和n-1轴线之间的公法线距离，即连杆长度，n=1,2,3,…,6[4]；θ为关节角度范围；vmax为最大关节速度.

表1　D-H参数表

由表1可得各变换矩阵为

式中：Sn=sinθn,Cn=cosθn，下同.因此，末端执行器的位姿方程为

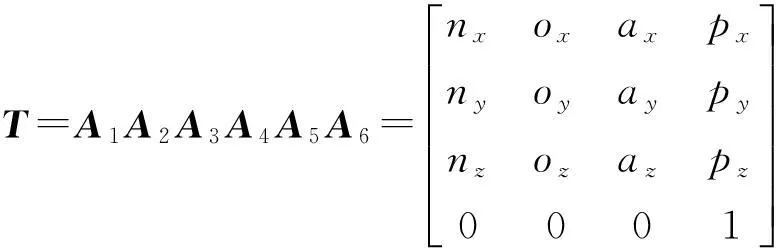
机器人运动学逆解的方法主要分为封闭解法和数值解法，封闭解法又分为代数解法和几何解法.封闭解法计算速度快、效率高，便于实时控制，而数值解法求解速度较慢，所以常用封闭解法求解.大多数工业机器人都可以应用Pieper准则，以简化逆解的运算[5-7].逆解方程为

(1)

1) 令式(1)左右两边矩阵的(3,4)元素(表示矩阵的第3行第4列，下同)相等，可得

S1(px-d6ax)+C1(py-d6ay)=0.

2) 令式(1)左右两边(2,4)和(1,4)元素分别相等，并化简为

(2a)

(2b)

3) 式(2)中，式(2a)×d4-式(2b)×a3,式(2a)×a3+式(2b)×d4,可得

式中:m=-a2-vC2-uC2,n=-uC2+vS2，则有θ3=ATAN2 (S3,C3).

4) 令式(1)左右两边(2,3)与(1,3)元素分别相等，可得

(3a)

(3b)

由式(3a)×S3-式(3b)×C3，可得

则有θ5=ATAN2 (S5,C5).

5) 令式(1)左右两边(3,3)元素相等，可得

则有θ4=ATAN2 (S4,C4).

6) 令式(1)左右两边(3,2)相等元素，可得

JC6-KS6=-C4.

式中：J=oxS1+oyC1,K=nxS1+nyC1，则

对于多解问题，首先，应根据关节运动范围对所求得的解进行取舍，然后，按照以下2种方法得到各关节的解.一是先求得多组关节角，再用“最短行程”得到一组最优解[2,8]；二是先求得θ1的多个解，再计算所求解与θ1当前角度值的欧氏距离，取其小者作为θ1的最优解，用此解求θ2，再利用欧氏距离求取θ2的最优解，其余关节角依此类推[9].最终可获得控制机器人实现目标位姿的1组最优关节角，2种最优解的取值方法，如图2所示.

2运动学仿真

为了验证所求解方程的准确性和可行性，使用Solidworks建立机器人的三维模型，并在Matlab中进行运动学仿真[10-11].仿真流程，如图3所示.

1) 螺旋线轨迹.螺旋线的轴心线垂直于基座标系(底座坐标系)的xy平面，在xy平面内的坐标为(1 200,0)，z坐标范围为0～720mm，螺旋线半径为100mm.机器人末端在按轨迹运动的过程中，其轴线z6始终竖直向下，从下往上运动.在仿真中，为整段螺旋线轨迹选定了720个关键点，即高度每增加1mm，机器人末端到达1个新的位姿.

螺旋线轨迹仿真过程三维动画截图与末端轨迹曲线，如图4所示.由图4可知：理论轨迹和实际轨迹重合，说明文中正逆解方程是正确的.

图3　仿真流程 图4　螺旋线轨迹　Fig.3　Simulation process Fig.4　Helical path

运动过程中各关节的角度值(θn)，如图5所示.由图5可知：在运动过程中，各关节角度值连续变化，且都在表1所列的关节角度范围内，说明文中所解方程是可行的，具有实用性.

(a) 关节1 (b) 关节2 (c) 关节3

(d) 关节4 (e) 关节5 (f) 关节6图5　螺旋线轨迹各关节角度值Fig.5　Each joint angle value of helical path

2) 球面轨迹.球心坐标为(900,-200,900)，半径为100 mm，球面轨迹是由半径不同的螺旋线组成.机器人末端在按轨迹运动的过程中，其轴线z6始终指向球心，从上往下运动.球面轨迹的关键点数为1 088个.

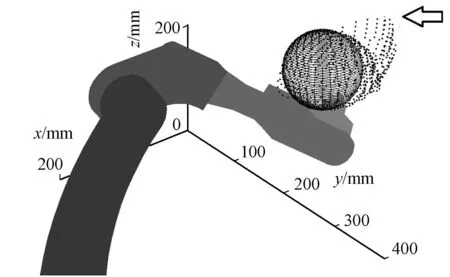
图6　球面轨迹Fig.6　Sphere path

球面轨迹仿真过程三维动画截图与末端轨迹曲线,如图6所示.图6中：机器人正在走球面的底部轨迹，点云为机器人的实际轨迹.由图6可知：箭头所指处的理论轨迹和实际轨迹中不重合，这是因为机器人在此处走球面轨迹和其末端轴线z6始终指向球心，不能同时完成，即运动奇异点，方程解得的关节5的角度值超出表1中的角度范围(-115°～115°)，所以程序采用关节5上一时刻的角度值，导致实际轨迹出现偏差.

运动过程中各关节的角度值，如图7所示.由图7可知：运动过程中各关节角度值连续变化，且都在表1的关节角度范围内.

(a) 关节1 (b) 关节2 (c) 关节3

(d) 关节4 (e) 关节5 (f) 关节6图7　球面轨迹各关节角度值Fig.7　Each joint angle value of sphere path

3结束语

对SA1400型机器人进行仿真，使机器人分别按螺旋线轨迹和球面轨迹运动，并对运动过程进行分析.实时的三维动态显示使仿真过程更加直观，关节角度值变化曲线图有利于对仿真过程进行分析.仿真结果证明文中所求得的解是正确、可行的，且文中的方法与思想也适用于其他关节型机器人.

参考文献：

[1]韩建海.工业机器人[M].3版.武汉:华中科技大学出版社,2015:60-86.

[2]王其军,杜建军.MOTOMAN机器人逆运动学新分析[J].哈尔滨工业大学学报,2010,42(3):451-454.

[3]王雪松,许世范,郝继飞.MOTOMAN机械手逆运动方程新的推导方法及求解[J].中国矿业大学学报,2001,30(1):73-76.

[4]蔡自兴.机器人学[M].2版.北京:清华大学出版社,2009：34-52.

[5]PAUL R,SHIMANO B,MAYER G.Differential kinematic control equations for simple manipulators[J].IEEE Trans SMC,1981,11(6):449-455.

[6]PIEPER D,ROTH B.The kinematics of manipulaor under computer control[J].Proceeding of the Second International Congress on Theory of Machines and Mechanisms,1969,2:159-169.

[7]JOHN J C.机器人学导论[M].3版.贠超,译.北京:机械工业出版社,2014：48-105.

[8]崔建国,宋爱国,黄惟一.遥操作系统中MOTOMAN-SV3机器人的运动建模研究[J].东南大学学报(自然科学版),2003,33(4):424-429.

[9]叶上高,刘电霆.机器人运动学逆解及奇异和多解的处理[J].机床与液压,2014,42(3):27-29.

[10]罗家佳,胡国清.基于Matlab的机器人运动仿真研究[J].厦门大学学报(自然科学版),2005,44(5):640-644.

[11]臧庆凯,李春贵,闫向磊.基于MATLAB的PUMA560机器人运动仿真研究[J].广西科学院学报,2010,26(4):397-400.

(责任编辑： 钱筠英文审校： 吴逢铁)

3D Kinematics Simulation of Six DOF Robot Using Matlab

LI Qing, XIE Yishou, ZHENG Lixin,ZHANG Yukun, ZHUANG Lihong

(Universities Engineering Research Center of Fujian Province Industrial Intelligent Technology and Systems,Huaqiao University, Quanzhou 362021, China)

Abstract：For the 3D kinematics modeling and simulation of SA1400 six degrees of freedom industrial robot, the robot kinematics equations are established and forward and inverse solutions are got. In order to verify the correctness of the equations and solutions. Firstly, solidworks is used to build 3D model of robot components. Then, forward and inverse solutions are programmed using Matlab, and models of robot components are imported. The 3D graphics functions of Matlab is used to display the 3D model of the robot, and do dynamic simulation of robot trajectory movement, while recording the change in the angle of each joint of robot during the simulation and suggesting irrational angle values and singular points. The results show that the process factually simulates the actual movement of the robot. The simulation results achieve the expected goal, and prove the accuracy and feasibility of solutions obtained from forward and inverse kinematics equations.

Keywords：3D simulation; industrial robot; six degrees of freedom; kinematics; Matlab

中图分类号：TP 391.9

文献标志码：A

基金项目：福建省科技厅科研计划资助项目(2013H2002)； 华侨大学研究生科研创新能力培育计划资助项目(1400422004)

通信作者：郑力新(1967-)，男，教授，博士，主要从事工业自动化技术、人工智能的研究.E-mail:zlxgxy@hqu.edu.cn.

收稿日期：2015-12-29

doi:10.11830/ISSN.1000-5013.2016.03.0299

文章编号：1000-5013(2016)03-0299-05