含混合常时滞的中立型系统稳定性

张玉凤， 周荣康

(1. 江苏建筑职业技术学院 机电工程学院， 江苏 徐州 221116；2. 华东理工大学 机械与动力工程学院， 上海 200237)



含混合常时滞的中立型系统稳定性

张玉凤1， 周荣康2

(1. 江苏建筑职业技术学院 机电工程学院， 江苏 徐州 221116；2. 华东理工大学 机械与动力工程学院， 上海 200237)

摘要：研究含混合常时滞的不确定中立系统的鲁棒稳定性问题，基于时滞分割方法，分别通过构造恰当的Lyapunov-Krasovskii泛函，并结合积分不等式处理技巧、自由权矩阵以及凸组合技术得到新的稳定性判据.通过数值仿真,将文中所得结论与已有的文献结果进行比较，验证结论的有效性.数值仿真表明：文中方法改善了已有文献的结果，降低了结论的保守性.

关键词：时滞系统； Lyapunov-Krasovskii泛函； 稳定性； 鲁棒性； 中立系统

对时滞系统的研究始于20世纪50至60年代，当时一些基本理论(系统方程解的唯一性、零解的稳定性理论)就已形成[1]，这些系统分析理论为后续的研究奠定了一定的基础，但是直到近二十年来，对时滞系统的研究才真正成为一个热点课题，尤其是在控制理论和控制工程领域[2-4].如何针对动态时滞模型进行稳定性分析，分析时滞对控制系统的影响或合理地利用系统的时滞信息，以提高控制系统的性能，具有重要的理论意义及现实意义[5-8].目前,关于时滞系统稳定性分析的多数结论是基于时滞相关条件而展开的.关于时滞相关条件的讨论，在时域内采用的研究方法主要涉及以下两个部分[9]：一是如何构造合适的Lyapunov-Krasovskii(L-K)函数；二是如何有效地处理L-K泛函的导数.对这两个方面研究的最终目标是使所得的时滞相关条件具有更低的保守性和有效性.本文针对含混合常时滞的中立型系统，基于时滞分割方法讨论系统的稳定性问题.针对具有结构不确定性的混合常时滞中立系统，基于时滞分割方法构造了新的L-K函数，结合积分不等式、自由权矩阵和凸组合技术推导出新的稳定性判定条件，并利用数值算例仿真验证了文中结论比现有文献具有更小的保守性.

1问题描述

考虑如下混合中立型系统，其离散时滞和中立时滞均为常数，即

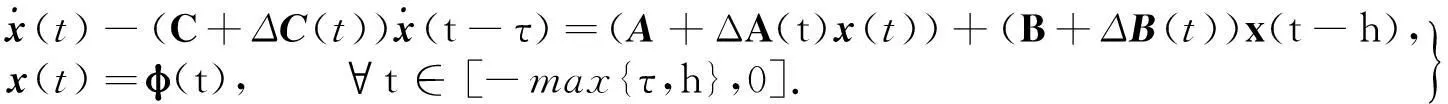
(1)

式(1)中：x(t)∈Rn是系统状态的向量；时滞h>0，为已知标量，且γ=max{τ,h}；φ(t)为初始向量函数；A，B，C为适当维数的已知常数矩阵;ΔA(t),ΔB(t),ΔC(t)为系统参数的不确定性,且满足条件

(2)

式(2)中：D,Ea,Eb,Ec为适当维数的常数矩阵;F(t)为未知时变矩阵,且满足

(3)

式(3)中：如果F(t)=0，则系统变为标称线性中立系统.

为保证系统稳定而估计离散时滞的最大上界范围，基于时滞分割法，将离散时滞进行平均分割，构造合适的L-K泛涵，结合积分不等式，从而得到保守性更低的结论.

2结论及其证明

首先,考虑系统(1)的标称系统的稳定性，即

(4)

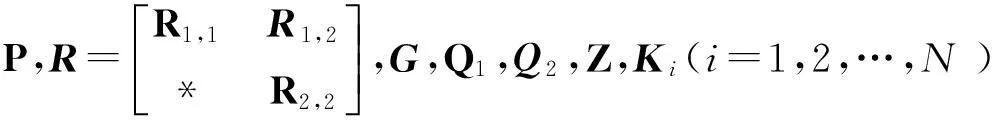
(5)

成立,则系统(4)渐近稳定.其中，

证明构造如下L-K泛函

(6)

其中，

计算L-K泛函V(t)沿系统(4)的导数，则有

(7)

(8)

(9)

(10)

由Jensen′s不等式,可得

(11)

(12)

(13)

进而可得

(14)

综合式(7)～(14)，可得

(15)

其中，

如果Φ<0，则由L-K稳定性定理可知，系统(1)的标称系统渐近稳定.由Schur补可知，Φ<0等价于定理1中的条件(5)，证毕.

依据定理1的证明思路,有如下推论.

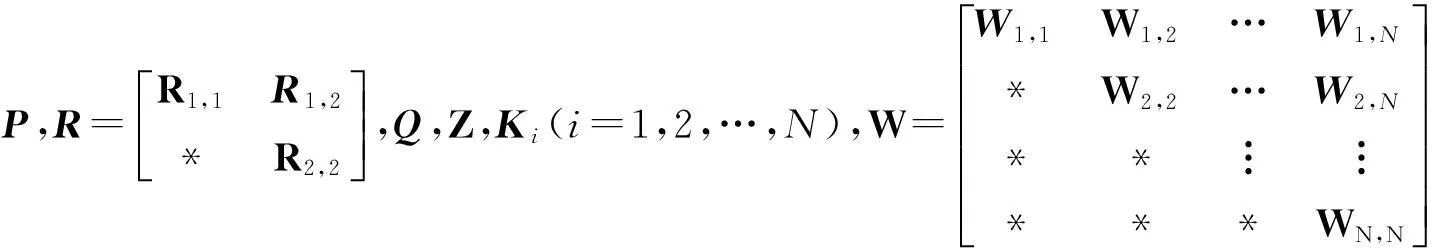
(16)

成立,则系统渐近稳定.其中,

3数值仿真与比较

通过数值仿真比较,说明文中方法改善了已有文献的结论.考虑如下中立系统[10],有

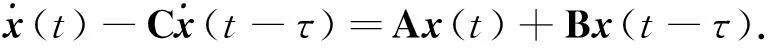
其中,

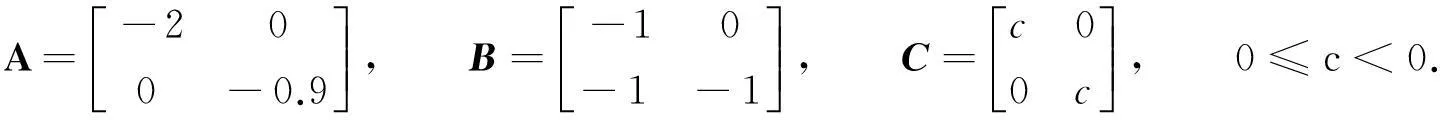
当c值不同时，推论1给出不同分割数下，保证系统稳定的最大时滞上界hM的值，同时，与文献[9-11]的结论进行比较，仿真结果如表1所示.由表1可知:相比已有文献[9-11]，文中推论1所得结果保守性明显降低，且随着分割数目的增加，保守性进一步降低，但是也会产生计算量随之增加的问题，为了折中结论的保守性和计算的复杂性，一般取N为较小的数值(2或3).

4结束语

研究了不确定中立型系统的鲁棒稳定性问题.针对含混合常时滞类型的不确定中立型系统，基于时滞分割法，把离散时滞区间[-h,0]均分成N份，针对不同的分割子区间构造了包含简单形式的泛函和三重积分形式的L-K函数.该方法有效利用了系统的时滞信息，降低了结论的保守性.数值仿真表明:文中方法改善了已有文献结果，降低了结论的保守性.

参考文献：

[1]朱莹,高其娜.依赖延迟线性时滞系统的稳定性判据[J].自动化学报,2013,39(12):2150-2153.

[2]HAMIDGM,REZAJM,MOJTABABY.Robuststabilizationforuncertainswitchedneutralsystemswithintervaltime-varyingmixeddelays[J].NonlinearAnalysis:HybridSystems,2014,13:2-21.

[3]KRISHNASAMYR,BALASUBRAMANIAMP.Adescriptorsystemapproachtothedelay-dependentexponentialstabilityanalysisforswitchedneutralsystemswithnonlinearperturbations[J].NonlinearAnalysis:HybridSystems,2015,15:23-36.

[4]洪雪梅,郑力新.采用工业以太网的直流电机控制系统[J].华侨大学学报(自然科学版),2012,33(5):506-509.

[5]HANQinglong.Robuststabilityofuncertaindelay-differentialsystemsofneutraltype[J].Automatica,2002,38(4):719-723.

[6]HEYong,WUMin,SHEJinhua,etal.Delay-dependentrobuststabilitycriteriaforuncertainneutralsystemswithmixeddelays[J].SystemsandControlLetters,2004,51(1):57-65.

[7]SUNJian,LIUGP,CHENJie.Delay-dependentstabilityandstabilizationofneutraltime-delaysystems[J].IntJofRobustandNonlinearControl,2009,19(10):1364-1375.

[8]张合新,惠俊军.基于时滞分割法的区间变时滞不确定系统鲁棒稳定新判据[J].控制与决策,2014,29(5):907-912.

[9]KWONOM,PARKJH,LEESM.Onstabilitycriteriaforuncertaindelay-differentialsystemsofneutraltypewithtime-varyingdelays[J].AppliedMathematicsandComputation,2008,197(1):864-873.

[10]ZHAO Zhengrong,WANG Wei,YANG Bin.Delay and its time-derivative dependent robust stability of neutral control system[J].Applied Mathematics and Computation,2007,187(2):1326-1332.

[11]QIU Fang,CUI Baotong,JI Yan.A delay-dividing approach to stability of neutral system with mixed delays and nonlinear perturbations[J].Applied Mathematical Modelling,2010,34(11):3701-3707.

(责任编辑： 黄晓楠英文审校： 黄心中)

Study on Stability of Neutral System With Interval Time-Varying Delay

ZHANG Yufeng1， ZHOU Rongkang2

(1. College of Mechanical Engineering， Jiangsu Vocational Institute of Architectural Technology, Jiangsu Xuzhou 221116, China;2. Machinery and Power Engineering College, East China University of Science and Technology, Shanghai 200237, China)

Abstract：The robust stability of uncertain neutral system with interval time-varying delay is studied. The new stability criteria are obtained by constructing appropriate Lyapunov-Krasovskii functional and combining integral inequality handling techniques, free weight matrix and convex combination. Numerical simulations are given to show the effectiveness of the proposed approach and the results of this paper are compared with the existing cited results. It shows that the method proposed in this paper improves the known results and shows less conservatism.

Keywords：time delay system; Lyapunov-Krasovskii functional; stability； robust； neutral system

中图分类号：TP 391.9

文献标志码：A

基金项目：国家自然科学基金资助项目(60874059)

通信作者：张玉凤(1972-)，女，副教授，主要从事电气工程技术的研究.E-mail:1337783864@qq.com.

收稿日期：2015-10-21

doi:10.11830/ISSN.1000-5013.2016.03.0386

文章编号：1000-5013(2016)03-0386-05