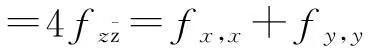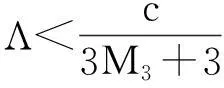双调和映照的单叶性与线性连结性

黄心中, 占龙俊

(华侨大学 数学科学学院, 福建 泉州 362021)



双调和映照的单叶性与线性连结性

黄心中, 占龙俊

(华侨大学 数学科学学院, 福建 泉州 362021)

摘要：假设F(z)=|z|2g(z)+h(z)为单位圆盘D={z||z|<1}上的双调和映照,其中，0

关键词：双调和映照; 凸映照; 线性连结性; 单叶性

1预备知识

在单连通区域Ω上,连续可微函数f(z)定义为

对于单连通区域Ω上的4阶连续可微复值函数F(z)=U(z)+iV(z),双调和映照的充分必要条件是ΔF是Ω上的调和映照,即Δ2(F(z))=Δ(ΔF(z))=0,对任意z=x+iy∈Ω都成立.由文献[2]可知：F(z)是单连通区域Ω上的双调和映照，当且仅当 F(z)=|z|2g(z)+h(z),其中，h(z)和g(z)是Ω上的复值调和映照.

对于单连通区域Ω,任意两点w1, w2∈Ω, 存在Ω上可求长曲线γ, 使得γ的弧长 l(γ)满足l(γ)≤M|w1-w2|.其中，M∈[1,∞),称Ω为M线性连结区域.

文献[4]对文献[3]所得的结论作进一步推广,得到参数化的成果,即定理B.

陈少林等[8]证明了定理C.

在上述基础上,文中研究双调和映照的单叶性与线性连结性的关系.对于双调和映照函数F(z)=

对于w1,w2∈h(D),γ1⊂h(D),其中，γ1为连结w1和w2的可求长曲线,由于h(D)是M1-线性连结区域,则有h(γ1)≤M1|w1-w2|.

对映照h-1(h(z))=z分别求微分,有

则有

接下来，证明F(D)是M2线性连结区域.令Γ1=H(γ1),有

因此

证明首先,要证明h(z)是单叶映照. 对于ξ=F(z)∈F(D), z=F-1(ξ)， 考虑到映照G(ξ)=h(F-1(ξ))=ξ-|F-1(ξ)|2g(F-1(ξ)),则只要证明G(ξ)是单叶映照.

对于ξ1,ξ2∈F(D),γ2⊂F(D),其中，γ2为连结点ξ1和ξ2的可求长曲线,由于F(D)是M3-线性连结区域,因此，l(γ2)≤M3|ξ2-ξ1|.

分别对映照F-1F(z))=z两边取微分得

由此推导出

综上所述，有

接下来，证明h(D)是线性连结区域.令Γ2=G(γ2),有

由此可得

证明易证F(z)是单叶调和映照且F(D)是9/7-线性连结区域.由定理2可知：h(z)是单叶调和映照且h(D)是9-线性连结区域.显然，h(z)为单叶的是凸映照.由此，定理2的结论是成立的.

参考文献：

[1]LEWYH.Onthenon-vanishingoftheJacobianincertainone-to-onemappings[J].BullAmerMathSoc,1936,42(10):689-698.

[2]ABDULHADIZ,MUHANNAY,KHURIS.Onunivalentsolutionsofthebiharmonicequations[J].InequalAppl,2005(5)：469-478.

[3]CHUAQUIM,HERNNDEZR.Univalentharmonicmappingsandlinearlyconnecteddomains[J].JMathAnalAppl,2007，33(2)：1189-1194.

[4]HUANGXinzhong.Locallyunivalentharmonicmappingswithlinearlyconnectedimagedomains[J].ChineseAnnMathSerA,2010,31(A5):625-630.

[5]王其文,黄心中.某些调和函数的系数估计与像区域的近于凸性质[J].华侨大学学报(自然科学版),2013,34(2):225-229.

[6]石擎天,黄心中.调和映照与其剪切函数的单叶性[J].华侨大学学报(自然科学版),2013,34(3):334-338.

[7]POMMERENKEC.Boundarybehaviourofconformalmaps[M],Berlin:Springer-Verlag,1992:106-107.

[8]CHENShaolin,PONNUSAMYS,RASILAAetal.Linearconnectivity,Schwarz-Picklemmaandunivalencycriteriaforplanarharmonicmappings[EB/OL].[2015-01-05]http://arxiv.org/abs/1404.4155.

[9]HERNNDEZR,MARTNMJ.Stablegeometricproperitiesofanalyticandharmonicfunctions[J].MathProcCambPhilSoc,2013,155(2):343-359.

[10]HUANG Xinzhong.Harmonic quasiconformal mappings on the upper half-plane[J].Complex Variables and Elliptic Equations,2013,58(7):1005-1011.

[11]夏小青,黄心中.一类双调和映照的单叶半径估计[J].华侨大学学报(自然科学版),2011,32(2):218-221.

[12]占龙俊,黄心中.调和映照与像域为线性连结的剪切函数的关系[J].华侨大学学报(自然科学版),2015,36(5):603-608.

(责任编辑： 陈志贤 英文审校： 黄心中)

Univalence and Linear Connetivity of Biharmonic Mappings

HUANG Xinzhong, ZHAN Longjun

(School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China)

Abstract：Suppose that F(z)=|z|2g(z)+h(z) is a biharmonic mapping on the unit disk D={z||z|<1}, and 0

Keywords：biharmonic mapping; covex mapping; linear connectivity; univalence

中图分类号：O 174.51; O 174.55

文献标志码：A

基金项目：国家自然科学基金资助项目(11471128)； 华侨大学中青年教师科研提升资助计划(ZQN-YX110)

通信作者：黄心中(1957-)，男，教授，博士，主要从事函数论的研究.E-mail:huangxz@hqu.edu.cn.

收稿日期：2015-10-28

doi:10.11830/ISSN.1000-5013.2016.03.0375

文章编号：1000-5013(2016)03-0375-05