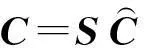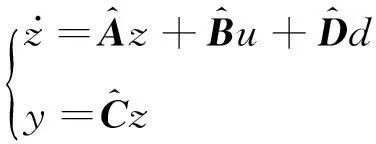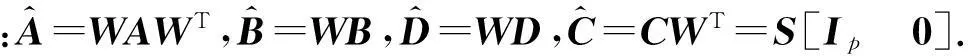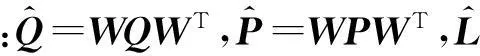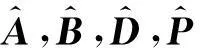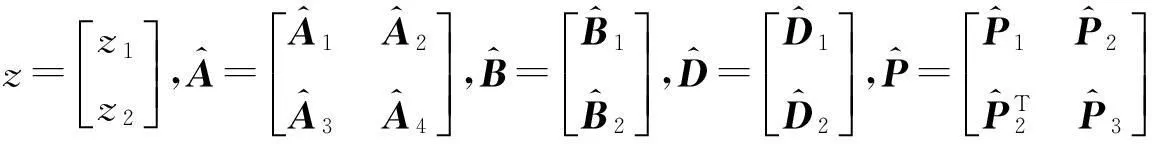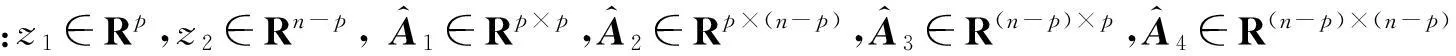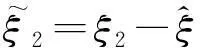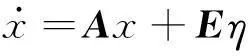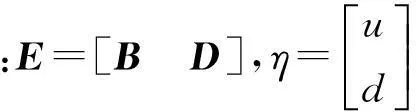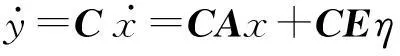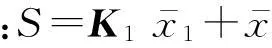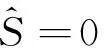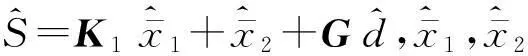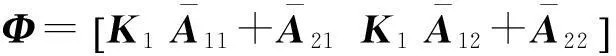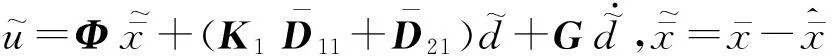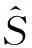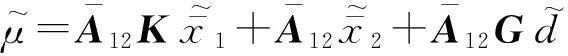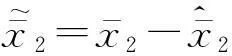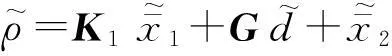基于观测器的不匹配未知输入系统的滑模控制

朱芳来， 于胜志， 张建成

(同济大学 电子与信息工程学院，上海 201804)



基于观测器的不匹配未知输入系统的滑模控制

朱芳来， 于胜志， 张建成

(同济大学 电子与信息工程学院，上海 201804)

摘要：对具有不匹配时变未知输入的线性系统，研究了基于观测器的滑模控制器设计方法.首先，设计了一种与控制输入无关、能直接抵消未知输入影响的降维观测器.通过该观测器估计系统状态，并提出了一种未知输入代数重构方法，进而利用高增益滑模观测器给出了未知输入一阶微分的渐近估计方法.最后，提出了一种基于系统状态估计、未知输入重构及未知输入一阶微分估计滑模控制器新的设计方法，并通过仿真分析，论证了该方法的可行性和正确性.

关键词：降维观测器；滑模控制器；未知输入重构；未知输入微分估计；高增益观测器

在控制系统的设计中，设计者们往往需要处理一些不确定因素，例如建模的非精确性所导致的部分模型参数的不确定性、模型参数扰动，外部未知输入的影响，执行器故障的发生等.从广义上来讲，这些不确定性都可以看成是系统的输入，由于它们都是未知的，所以可以统称之为系统的未知输入.由于在实际系统中，这些未知的因素普遍存在，所以，在控制系统的设计中，无论是控制器设计，还是观测器设计，如何处理好未知输入对设计的不良影响，成为设计者们的主要考虑问题之一，而这样的设计，通常称之为鲁棒设计.

滑模控制器由于有着对参数和外部扰动的不敏感性，使得它成为处理具有不确定性，非线性项及有界外部未知输入系统最为有效的鲁棒控制方法之一[1].滑模控制在处理匹配未知输入方面，可以直接抵消未知输入的影响，而达到平衡状态的渐近收敛稳定.而对于绝大多数的实际系统，未知输入往往与控制输入具有不同通道，这样的未知输入称之为不匹配未知输入.针对不匹配未知输入抑制的研究，成为鲁棒控制的研究热点之一[2-8].文献[8]提出了基于高阶滑模观测器的滑模控制设计方法，其主要优点是把时变未知输入估计引入到控制器，然而其设计的高阶滑模观测器结构太过复杂.

对观测器设计而言，未知输入观测器(UIO)是鲁棒观测器设计的一类方法，受到了国内外学者们的极大关注，早期的研究主要是在输入未知的情况下也能够估计系统状态的观测器[9]，后来发展到能对系统状态和未知输入同时估计的观测器设计[10].现在应用比较广泛的是高增益观测器和高阶滑模观测器，它们能够精确估计系统状态和未知输入[11-12].例如文献[12]提出了一种利用高增益滑模观测器来估计系统状态和重构其未知输入的方法,并提出了用高阶滑模观测器来估计系统输出微分信息的方法.

在文献[8]的提示下，本文针对具有不匹配时变未知输入的系统，提出了一种新的基于系统状态估计、未知输入重构及其一阶微分估计的滑模控制器的设计方法.本文创新点在于①提出了一种与控制输入无关，且能直接消去未知输入影响的鲁棒降维观测器设计方法，为基于观测器的滑模控制器设计带来便利；②使用了一种未知输入代数重构方法，并基于未知输入的重构，结合二阶高增益滑模观测器的基础上，提出了未知输入一阶微分渐近收敛的估计方法；③通过纳入状态估计，未知输入重构及其未知输入一阶微分估计的信息，提出了一种处理时变不匹配未知输入的鲁棒滑模控制器设计方法.

1系统描述及背景知识

考虑具有未知输入的线性时不变系统

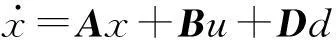
y=Cx

(1)

式中：x∈Rn为状态向量；y∈Rp(1≤p

假设1：(A,B)可控的.

假设2：rank(C[BD])=rank([BD])=m+q.本文针对具有此类属性的特定系统设计降维观测器，并给出了未知输入重构的方法.

注1：对于系统(1)，由于输入矩阵B和未知输入矩阵D线性无关，所以系统(1)称之为不匹配未知输入系统.对具有不匹配干扰或者未知输入系统进行鲁棒控制设计，是目前鲁棒控制研究的热点之一.

(2)

(3)

假设5：rank([A12D11])=rank(A12)，即为了补偿式(2)中未知输入.

本文的主要目的是设计基于状态估计和未知输入重构及未知输入微分估计的滑模控制器，使得一部分状态渐近收敛稳定，而另一部分状态是邻域收敛稳定.为此，设计了降维观测器来估计系统的状态，并在此基础上提出了未知输入重构方法，然后利用高增益滑模观测器给出了未知输入的一阶微分的渐近收敛估计.

2系统状态的估计

提出一种降维观测器设计方法来估计系统的状态.

引理1[12]：假设2和假设3成立的充分必要条件是：对任意的对称正定矩阵Q∈Rn×n,如下的矩阵方程

(4)

关于正定矩阵P∈Rn×n，矩阵H∈R(q+m)×p和L∈Rn×p有解.

(5)

(6)

对系统状态作如下变换

(7)

其中ξ1∈Rp,ξ2∈Rn-p.所以,式(5)转化为

(8)

定理1:在假设2～假设4的情况下，如下系统

(9)

注2：由式(9)所确定的降维观测器，具有这样的特点：一是跟控制输入无关，这给基于观测器的滑模控制器设计带来便利，这使得控制器设计和观测器设计具有独立性.同时，降维观测器的误差动态方程不受未知输入的影响，这表明降维观测器对未知输入具有极强的鲁棒性.

3未知输入的重构

系统状态方程(1)可以改成

(10)

由假设2可知，矩阵CE的广义逆矩阵为(CE)+=[(CE)T(CE)]-1(CE)T.所以可得

由上式，可以得到η的重构方法

(11)

如下的二阶高增益滑模观测器，提供了有界光滑信号r的一阶微分在有限时间内的精确估计[13]

(12)

4基于观测器的控制器设计

(13)

基于系统状态估计，未知输入重构及未知输入微分估计，提出滑模控制器设计如

(14)

定理2:由式(14)定义的滑模控制器，可以使系统的动态特性在有限时间内达到观测滑模面式(13)上.

证明：对S求导则有

(15)

将式(14)代入式(15)，整理之后有

(16)

另一方面式(2)可以等价地写为

(17)

将式(16)代入式(17)，整理之后得到

(18)

综上所述，系统的具体流程框如图(1)所示.

图1　系统的流程框图

5系统仿真

考虑如下的系统：

对于本例，取未知输入为d=sin(3t).由降维观测器所给出的系统状态估计见图2，系统未知输入的重构及未知输入的一阶微分估计效果如图3所示.图4给出了滑模控制信号曲线.状态控制效果如图5～图6所示，由图5可以看出控制器能将系统状态x1,x2控制渐近收敛到0，而图6表明闭环系统状态x3有界.

图2　系统状态及其估计值

图3　未知输入d重构及一阶微分估计

图4　控制器u的输出

图5　引入控制器后的系统状态x1,x2及其估计值

Fig.5The system statex1,x2and their estimations after the introduction of the controller

图6　引入控制器后的系统状态x3及其估计值

Fig.6The system statex3and its estimation after the introduction of the controller

6结论

针对具有不匹配时变未知输入的系统，研究了基于观测器的滑模控制器设计方法.所提出的降维观测器跟控制输入信号无关，使得控制器设计和观测器设计能独立实施.控制器设计，通过引入状态的估计，未知输入重构及其未知输入一阶微分的估计，提出了能处理时变不匹配未知输入的滑模控制器设计方法.为此，提出了基于未知输入重构去渐近收敛估计未知输入一阶微分的思想和方法.如何将结论上升到非线性系统，是值得进一步考虑的研究内容.

参考文献:

[1]Man Z H, Paplinski A P, Wu H R. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators[J].IEEE Transactions on Automatic Control,1994,39(12): 2464.

[2]Kim K S,Park Y,Oh S H. Designing robust sliding hyperplanes for parametric uncertain systems: a Riccati approach[J].Automatica,2000,36(7):1041.

[3]Silva J M A, Edwards C, Spurgeon S K. Sliding-mode output-feedback control based on LMIs for plants with mismatched uncertainties[J].IEEE Transactions on Industrial Electronics, 2009,56(9):3675.

[5]Gao Z, Liao X Z. Integral sliding mode control for fractional-order systems with mismatched uncertainties[J]. Nonlinear Dynamics, 2013, 72(1): 27.

[6]Mondal S, Mahanta C. Chattering free adaptive multivariable sliding mode controller for systems with matched and mismatched uncertainty[J]. ISA Transactions, 2013, 52(3): 335.

[7]Yang J, Li S H, Yu X H. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer[J]. IEEE Transactions on Industrial Electronics,2013, 60(1): 160.

[8]de Loza A F, Bejarano F J, Fridman L. Unmatched uncertainties compensation based on high-order sliding mode observation[J].International Journal of Robust and Nonlinear Control 2013,23:754.

[9]韩冬，朱芳来.一类未知输入系统的降维观测器设计[J].上海交通大学学报，2012,46(11): 1779.

HAN Dong,ZHU Fanglai. Reduced-order observer design for system with unknown inputs[J].Journal of Shanghai Jiaotong University, 2012,46(11):1779.

[10]Yang J Q, Zhu F L, Sun X J. State estimation and simultaneous unknown input and measurement noise reconstruction based on associated observers[J]. International Journal of Adaptive Control and Signal Processing, 2011,27(10): 846.

[11]de Loza A F, Punta E, Fridman L,etal. Nested backward compensation of unmatched perturbations via HOSM observation[J].Journal of the Franklin Institute—Engineering and Applied Mathematics,2014, 351(5): 2397.

[12]Zhu F L. State estimation and unknown input reconstruction via both reduced-order and high-order sliding mode observers[J]. Process Control, 2012,22(1): 296.

[13]Levant A.High-order sliding modes: differentiation and output feed-back control[J]. International Journal of Control, 2003,76: 924.

[14]Edwards C,Spurgeon S K.Sliding mode control[M].London: Taylor and Francis,1998.

Observer-based Sliding Mode Control for System with Mismatched Unknown Input

ZHU Fanglai, YU Shengzhi, ZHANG Jiancheng

(College of Electronics and Information Engineering, Tongji University, Shanghai 201804, China)

Abstract：An investigation was made into the sliding mode control design method for a class of linear system with unmatched time-varying unknown inputs. A reduced-order observer was developed to be independent of the control inputs and able to overcome the influence of the unknown inputs. Moreover, an algebraic unknown input reconstruction method based on state estimation was developed. Besides, an estimation method of the first-order derivatives of the unknown inputs was proposed by means of a high-gain sliding mode observer. Finally, based on the estimation of the system states, the reconstruction of the unknown input and the first derivative estimation, a novel sliding mode controller was constructed，and a simulation analysis validated the effectiveness of the proposed method.

Key words：reduced-order observer; sliding mode controller; unknown input reconstruction; unknown input differential estimation; high-gain sliding mode observer

文献标志码：A

中图分类号：TP15

基金项目：国家自然科学基金(61074009)

收稿日期：2015—06—02

第一作者： 朱芳来(1965—)，男，教授，博士生导师，工学博士，主要从事研究方向为观测器设计，滑模控制等.

E-mail：zhufanglai@tongji.edu.cn