超高层建筑结构组合调谐风振控制系统

赵　昕, 王立林， 郑毅敏

(1. 同济大学 土木工程学院， 上海 200092； 2. 同济大学建筑设计研究院(集团)有限公司， 上海 200092)



超高层建筑结构组合调谐风振控制系统

赵昕1,2, 王立林1， 郑毅敏1,2

(1. 同济大学 土木工程学院， 上海 200092； 2. 同济大学建筑设计研究院(集团)有限公司， 上海 200092)

摘要：为充分利用调谐液体阻尼器(TLCD)的经济性和调谐质量阻尼器(TMD)的高效性，提出一种TLCD与TMD相结合的组合调谐阻尼器(CTD)，从理论上说明CTD的合理性，推导其运动方程，引入协同损失因子评价其减振性能，并与TLCD和TMD的减振效果进行对比分析.研究表明：CTD不同参数配置时，协同损失因子不同，可达35%；相同参数配置下，CTD减振效果介于TMD和TLCD之间.综合经济和效率因素，CTD是一种很有竞争力的减振手段，具有广阔的工程应用前景.

关键词：超高层建筑； 组合调谐阻尼器； 风振控制； 协同损失因子； 调谐质量阻尼器； 调频液柱阻尼器

超高层建筑结构的自振周期接近风荷载的卓越周期，在脉动风荷载作用下的风致振动(抖振)除造成结构疲劳损伤外，还会引起居住者不舒适感.为了改善超高层建筑结构的风振舒适度性能，工程中常需安装振动控制装置，常用的包括调谐质量阻尼器(TMD)和调谐液体阻尼器(TLCD)[1].传统的工程案例通常采用单一类型的阻尼器，这种做法存在一定局限性：采用TMD时，所需质量块体积大，占用空间多，造价高；采用TLCD时，除拟需的消防水箱还必须额外配置水箱，占用大量空间.为了降低阻尼器造价，实际工程中也有采用水箱充当TMD质量块的案例：澳大利亚的悉尼电视塔上安装了两个TMD来减小电视塔的第一、二振型风振反应，用于控制第一振型响应的TMD是悬吊在塔楼顶部重达180 t 的水箱，这是第一个用水箱来代替质量块的尝试.也有学者对TMD与TLCD的结合使用进行了研究.XU[2]等提出了调谐液柱/质量阻尼器(tuned liquid column mass damper, TLCMD)装置，该装置中TLCD除发挥减振作用外，其U型水箱及其所储液体还作为TMD的运动质量.周福霖、黄东阳[3]等在XU研究的基础上，借鉴兰文武[4]提出的混合水箱装置(multiple tuned liquid column dampers, MTLDs)的设计方法，提出了充分利用TLCMD凹部空间的新型混合调频类阻尼器.为了充分利用TLCD的经济性和TMD的高效性，提出了一种TLCD和TMD结合使用的CTD，并研究了其减振性能.

1组合调谐阻尼器

1.1组合控制系统减振原理

TLCMD是建立在TLCD充当TMD的减振质量进而降低阻尼器造价的思想基础上的.当忽略液体的晃动效应时(水箱满装)，TMD保持运动特性；当液体的晃动效应不能忽略时(水箱不装满)，TLCD会对TMD的运动产生影响，整个装置可等效为受控的TMD.该方案中TLCD与TMD的运动是相互耦联的，结构受振时引起TMD运动进而引起TLCD运动，当二者运动不同步时，液柱的晃动可能对阻尼器系统起抑制作用[2].为了克服该局限性，提出组合调谐阻尼器(CTD)，如图1所示.1代表结构，2代表阻尼器装置，其中TLCD由消防水箱充当，位置根据消防要求和结构特点确定；TMD和TLCD直接设置在结构上，二者的运动是相互独立的，均直接控制结构的振动，减振原理如图2所示.2a为将超高层建筑简化后得到的质点串模型，记为“结构1”;图2b为在“结构1”上仅布置TMD，此时整体体系亦可视为质点串模型，记为“结构2”;图2c为在“结构1”上仅布置TLCD，此时整体体系亦可视为质点串模型，记为“结构3”;图2d有两种含义：一是表示在“结构2”上仅布置TLCD，此时整体体系亦可视为质点串模型，记为“结构4”，二是表示在“结构3”上仅布置TMD，此时整体体系亦可视为质点串模型，记为“结构4”.可以看出，借助“中间结构”的概念能够解释CTD-结构系统的合理性.需注意的是，CTD在实际工程中发挥作用时，其所包含的TMD和TLCD是同步、独立工作的，不存在先后之分.图中，mi,ki,ci(i=1,2,…,n)，分别为各质点质量、刚度和阻尼.

aCTD控制系统示意图bTLCD示意图

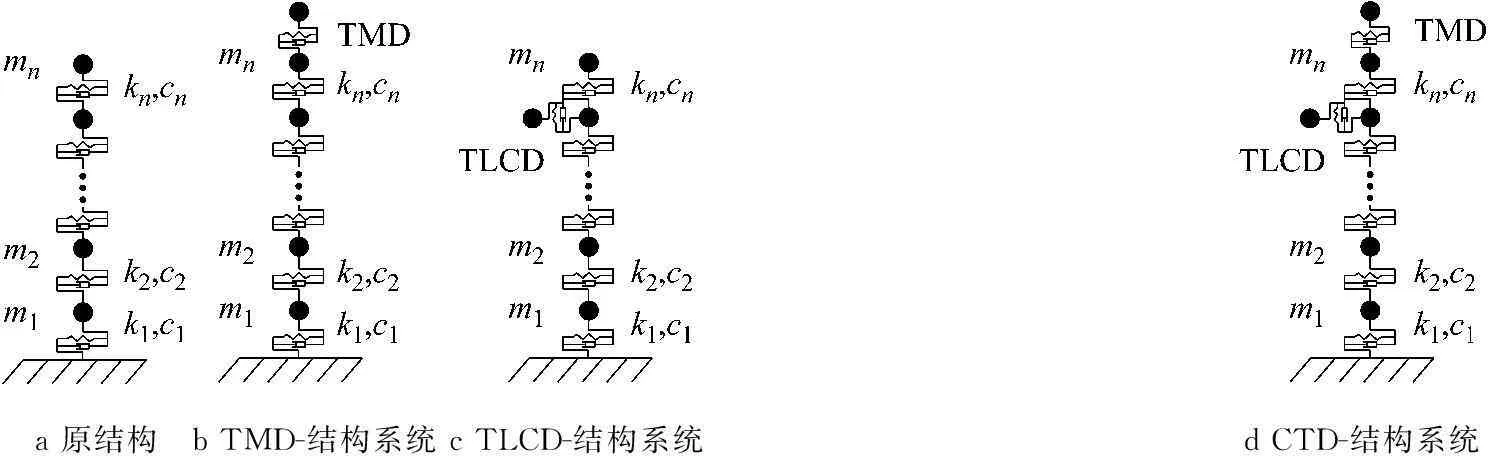
图1　组合调谐控制系统

图2CTD原理示意图

Fig.2Theory of combined tuned damper

1.2组合控制系统运动方程

CTD-结构体系的运动方程可得

TMD组员运动方程为

(1)

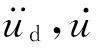
TLCD运动方程为

(2)

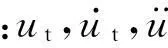
结构运动方程为

(3)

综合式(1)—式(3) 则可获得结构—CTD体系的综合控制方程,即

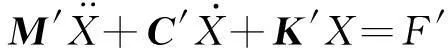
(4)

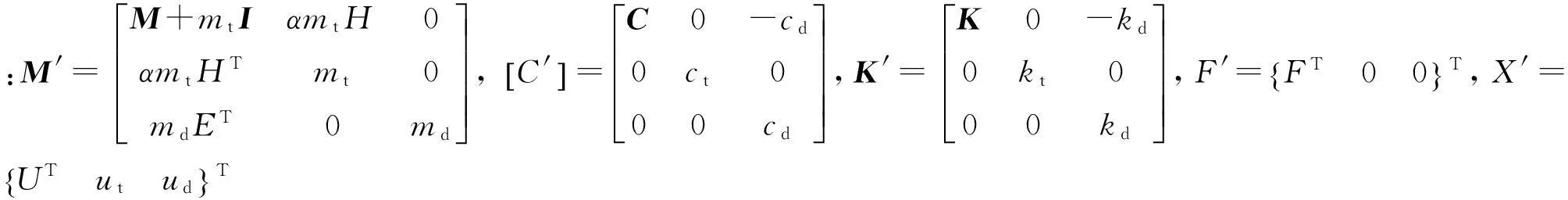
2CTD减振效果研究

2.1CTD—结构系统

方便起见，以一个单质点案例对CTD的性能进行探究，如图3所示.图中：D为结构直径；Z为高度；m,c,k分别为质量，阻尼和刚度.对其运动方程分析如下：

(5)

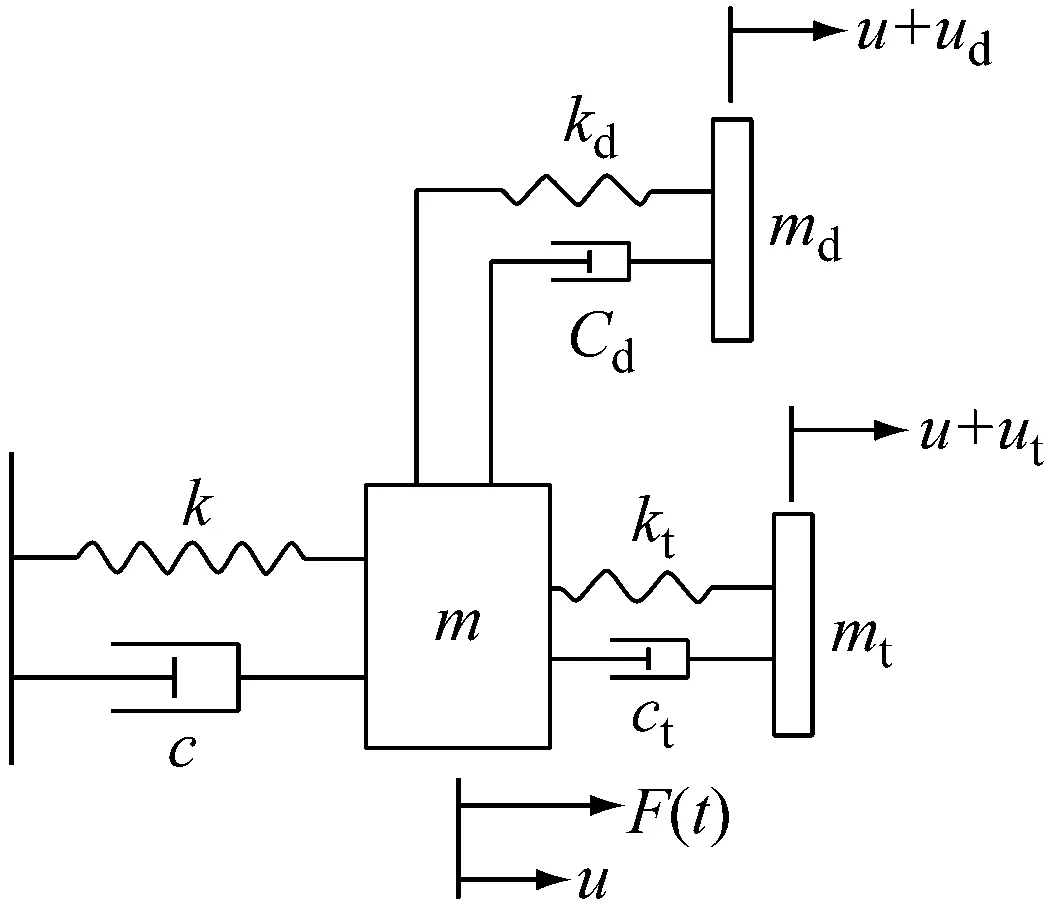
图3　单自由度结构-CTD系统示意图

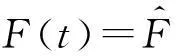
(6)

(7)

求解式(7)并将结果平方可得到频率响应函数，即

(8)

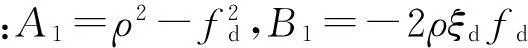
风荷载采用Davenport谱，功率谱密度如下：

(9)

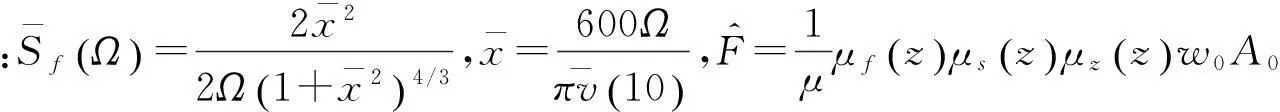
(10)

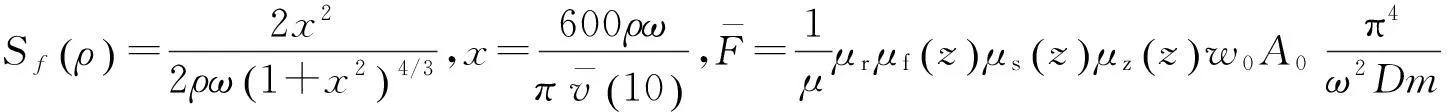
(11)

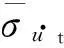
2.2阻尼器参数分析

2.2.1CTD参数敏感性分析

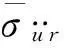
(12)

(13)

根据文献[5]的建议，顶部装有大质量块的塔体结构基频周期可表示为

(14)

而框架结构的基频周期可表示为

(15)

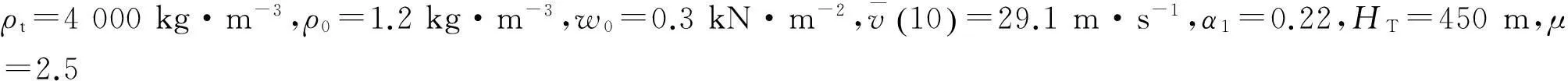
(16)

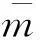
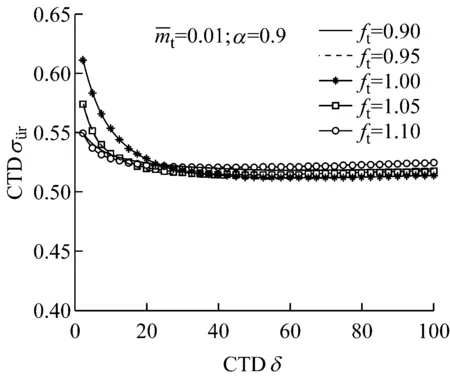
图4　不同频率比下水头损失系数对加速度减振影响

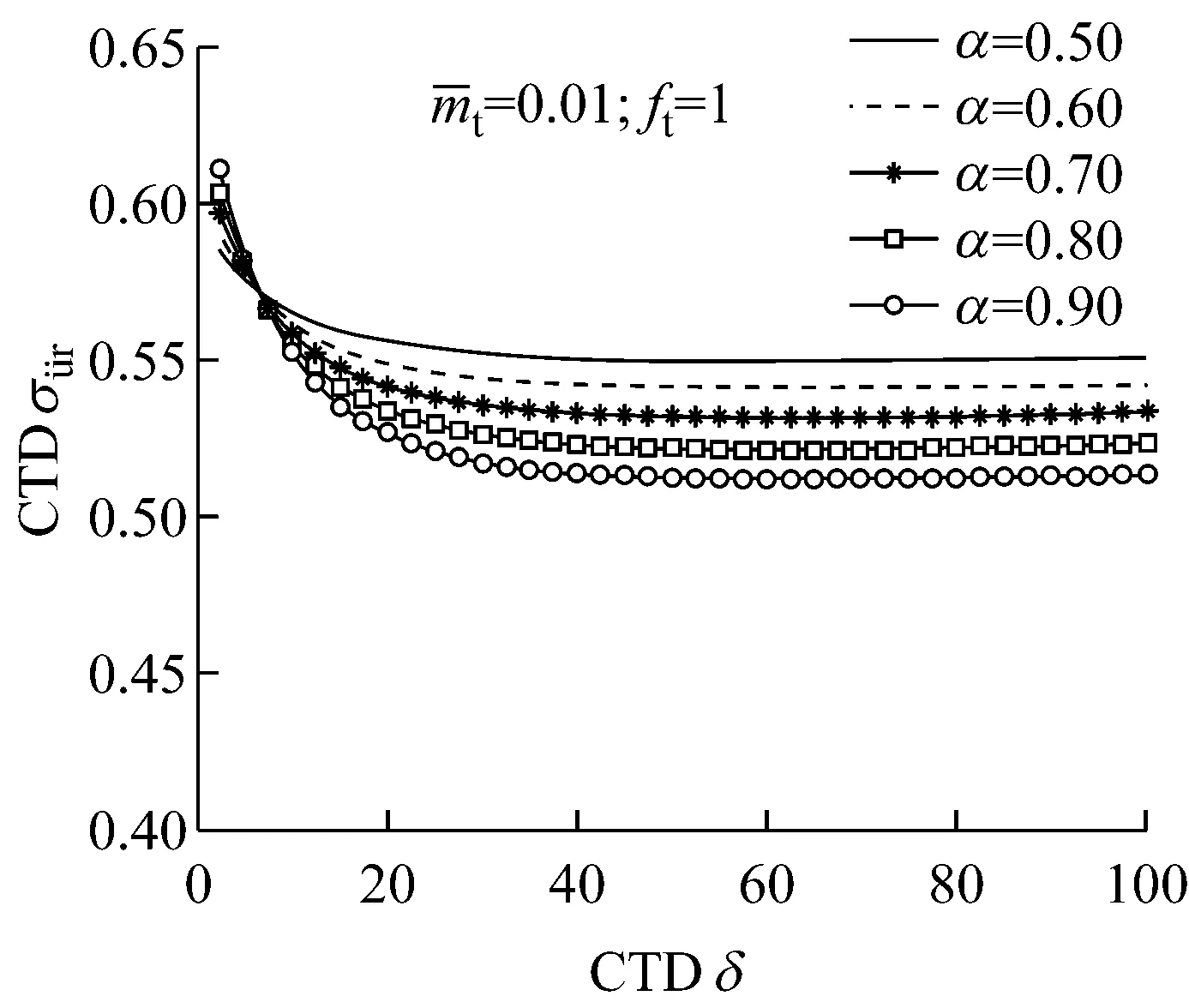
图5　不同长度系数下水头损失系数对加速度减振影响

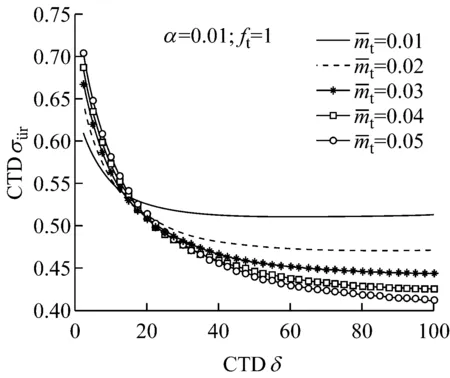
图6　不同质量比下水头损失系数对加速度减振影响

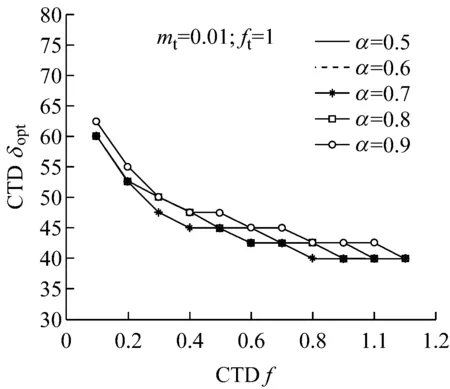
图7　加速度减振最优水头损失系数 (ft=1, mt=0.01)

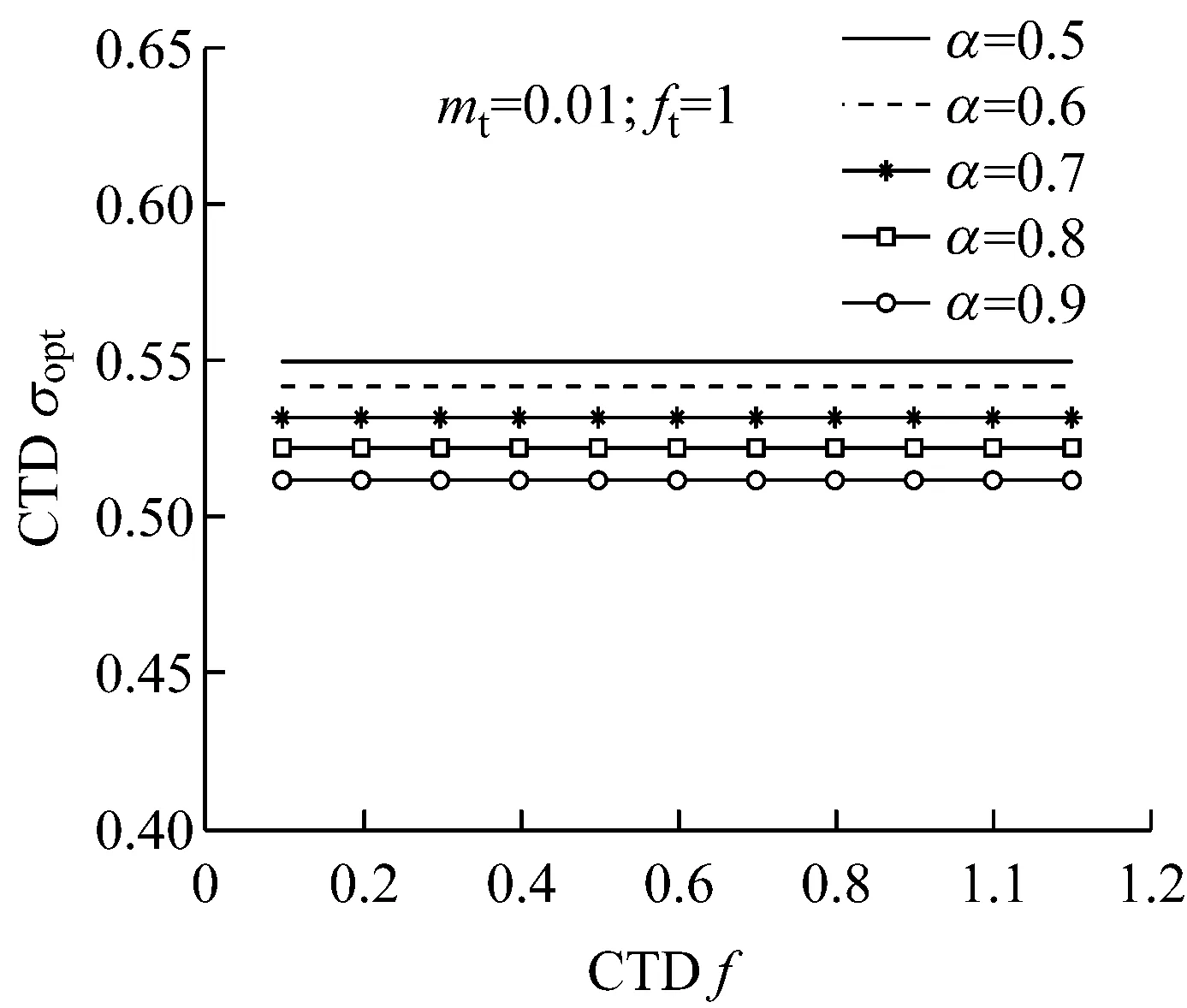
图8　最优水头损失下加速度减振效果

Fig.8Reduction in acceleration corresponding to the optimal head loss forft=1 andmt=0.01

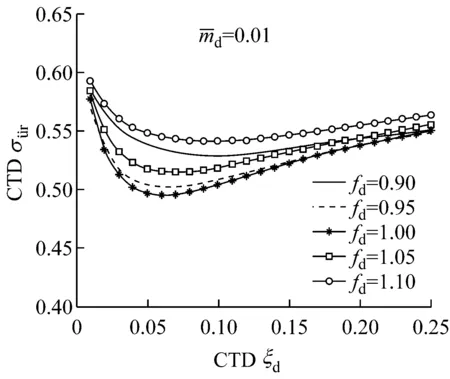
图9　不同频率比下阻尼比对加速度减振影响

Fig.9Influence of the damping ratio of the TMD on the reduction in acceleration with differentfd

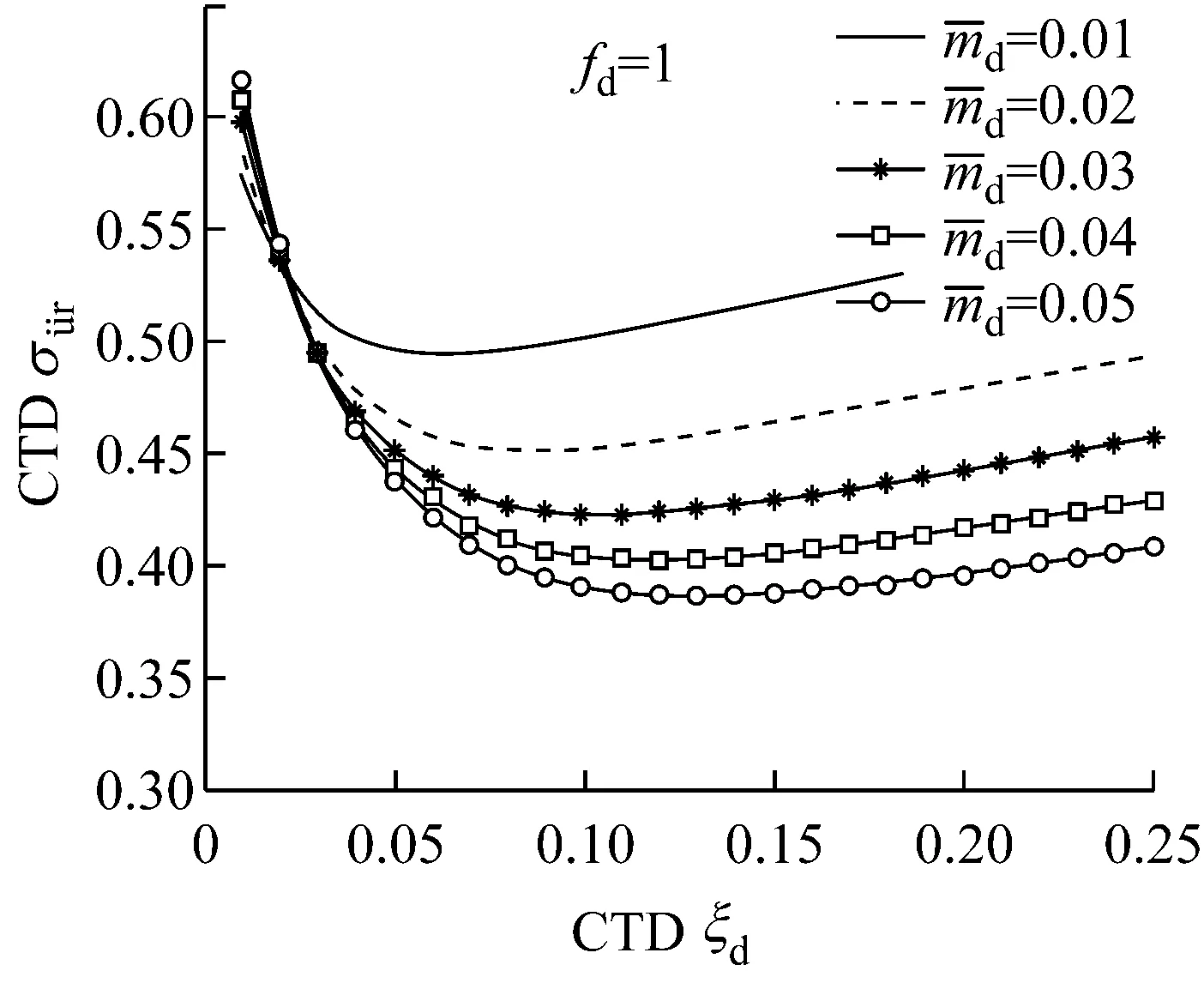
图10　不同质量比下阻尼比对加速度减振影响

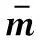
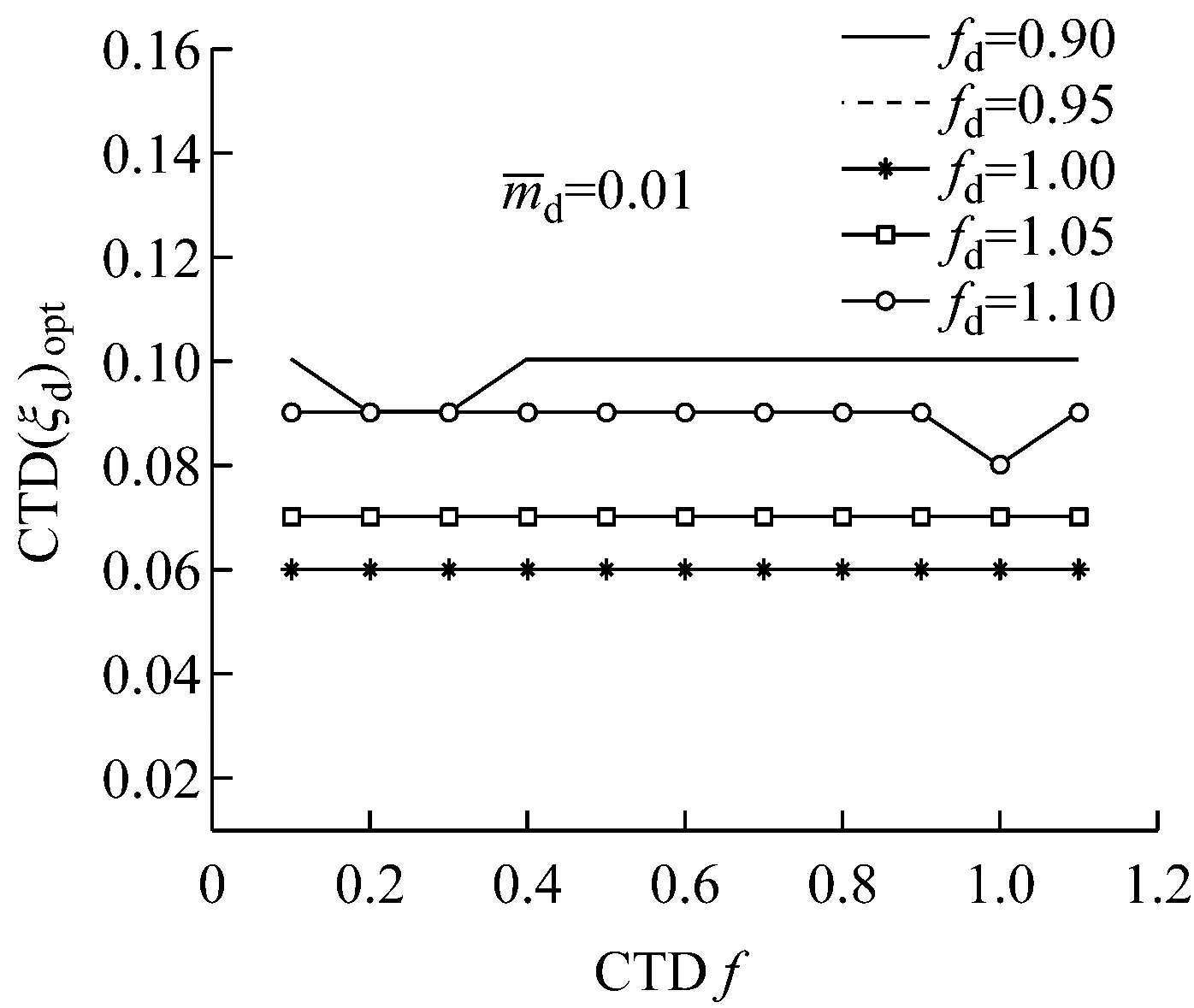
图11　加速度减振最优阻尼比

Fig.11Optimal damping ratio of the TMD for the maximum reduction in accelearation formd=0.01

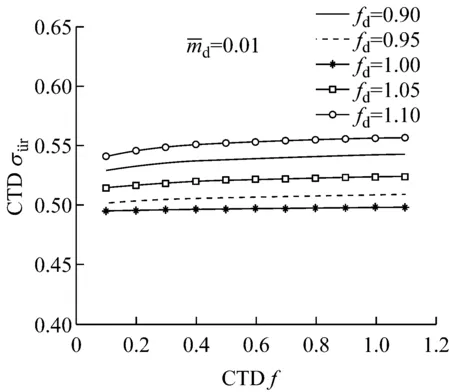
图12　最优阻尼比下加速度减振效果

2.2.2CTD与TMD/TLCD作用效果对比

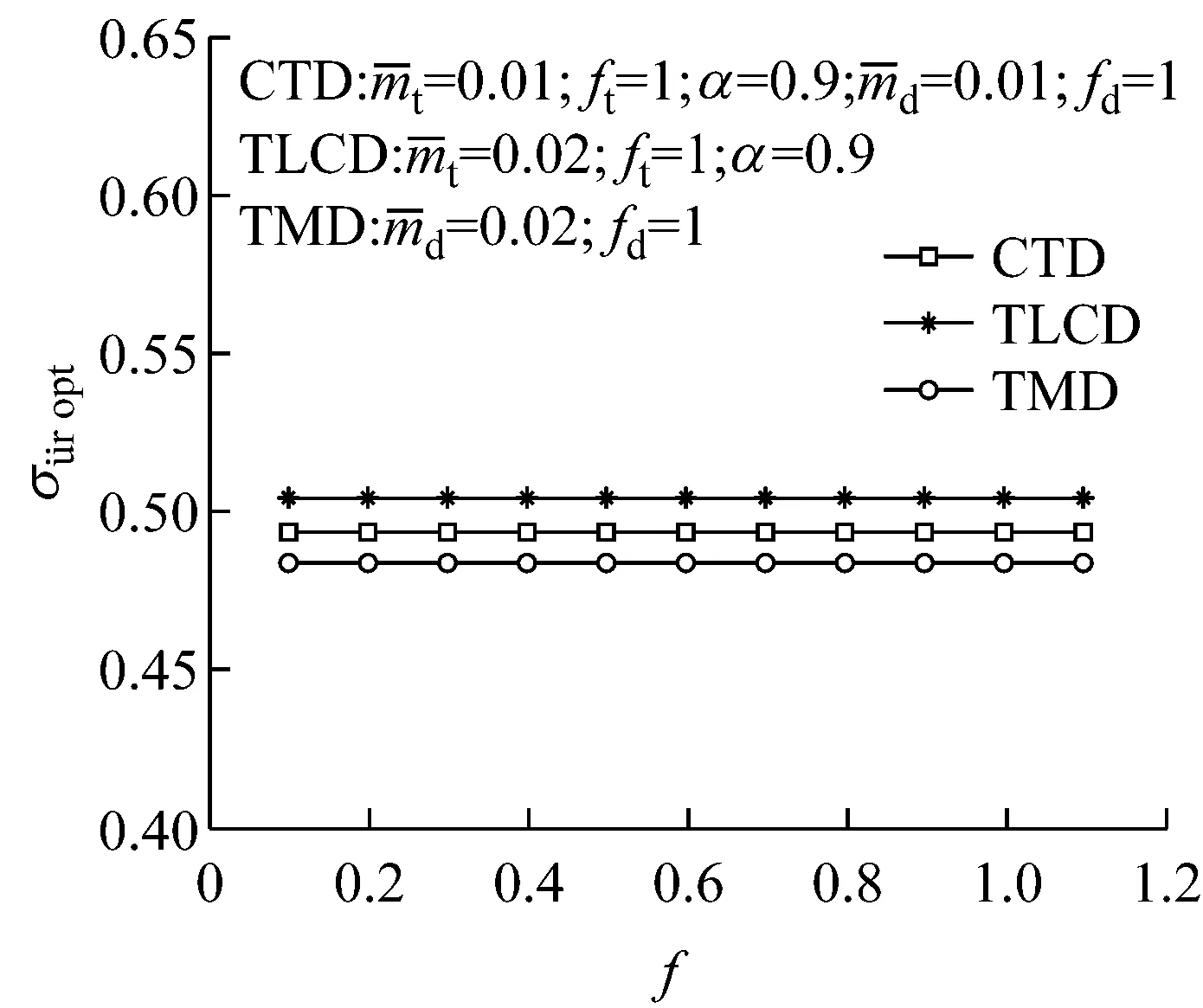
图13　最优参数下加速度减振效果对比

2.3CTD协同损失分析

从CTD的工作原理可知其包括的TMD和TLCD均直接控制结构的振动，二者相互独立，并不藕联，但因二者同时对主体结构起作用，主体结构振动状态的改变，会引起二者减振效率的降低.因此，虽然CTD中TMD和TLCD相互独立，却因二者同时作用于同一结构而产生相互影响(如图14示意).为便于分析，将这种由结构的受控引起的CTD减振效率的损失定义协同损失因子：

(17)

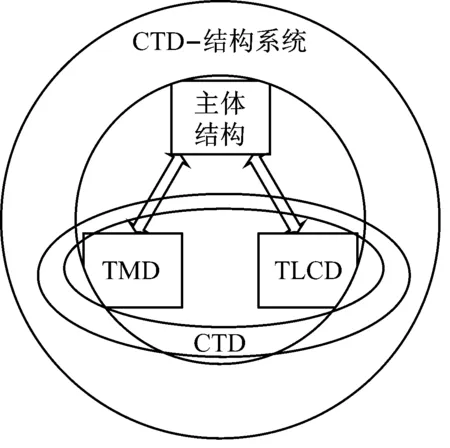
图14　CTD-结构系统相互关系

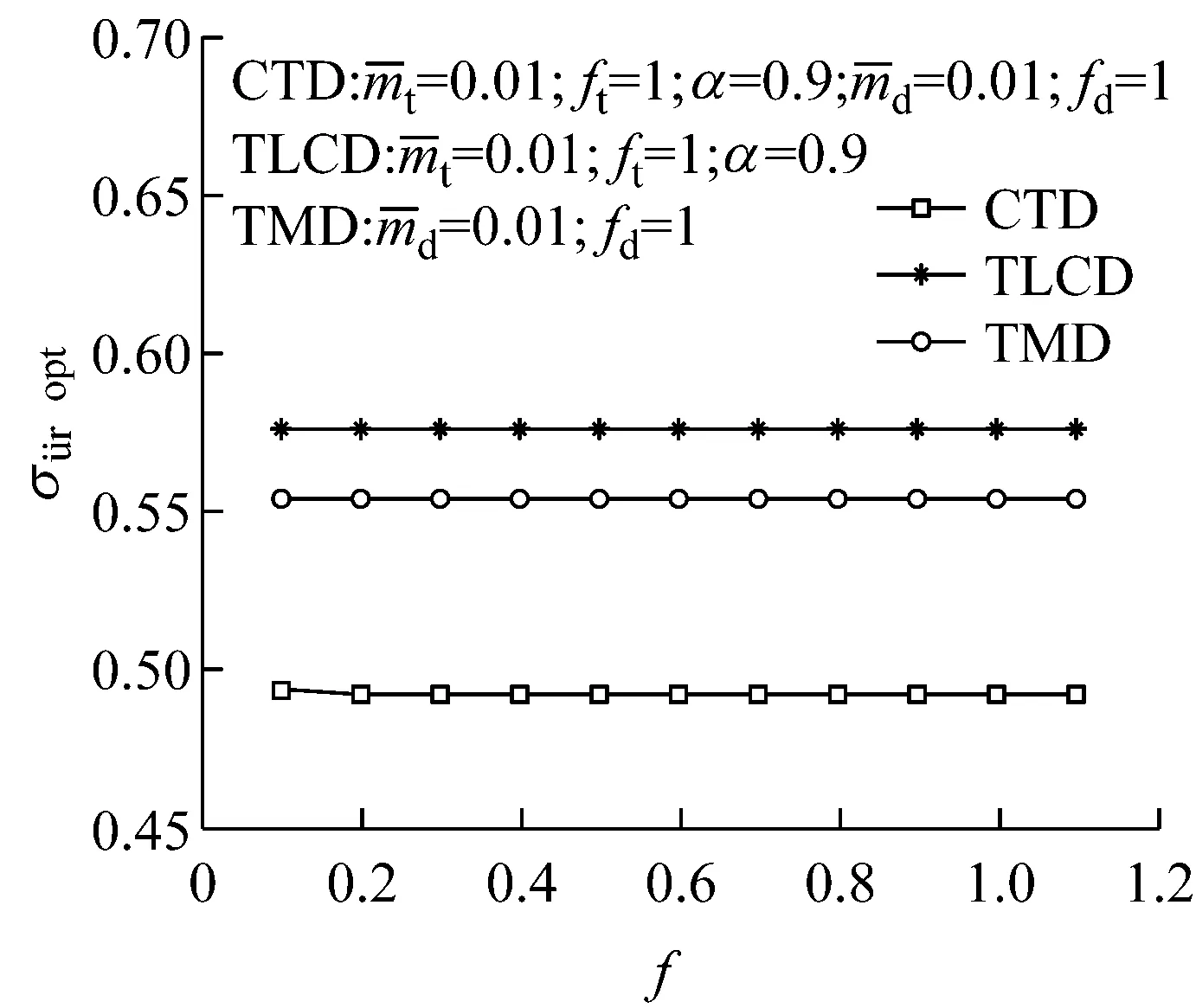
图15　CTD及其组员TLCD/TMD加速度减振效果

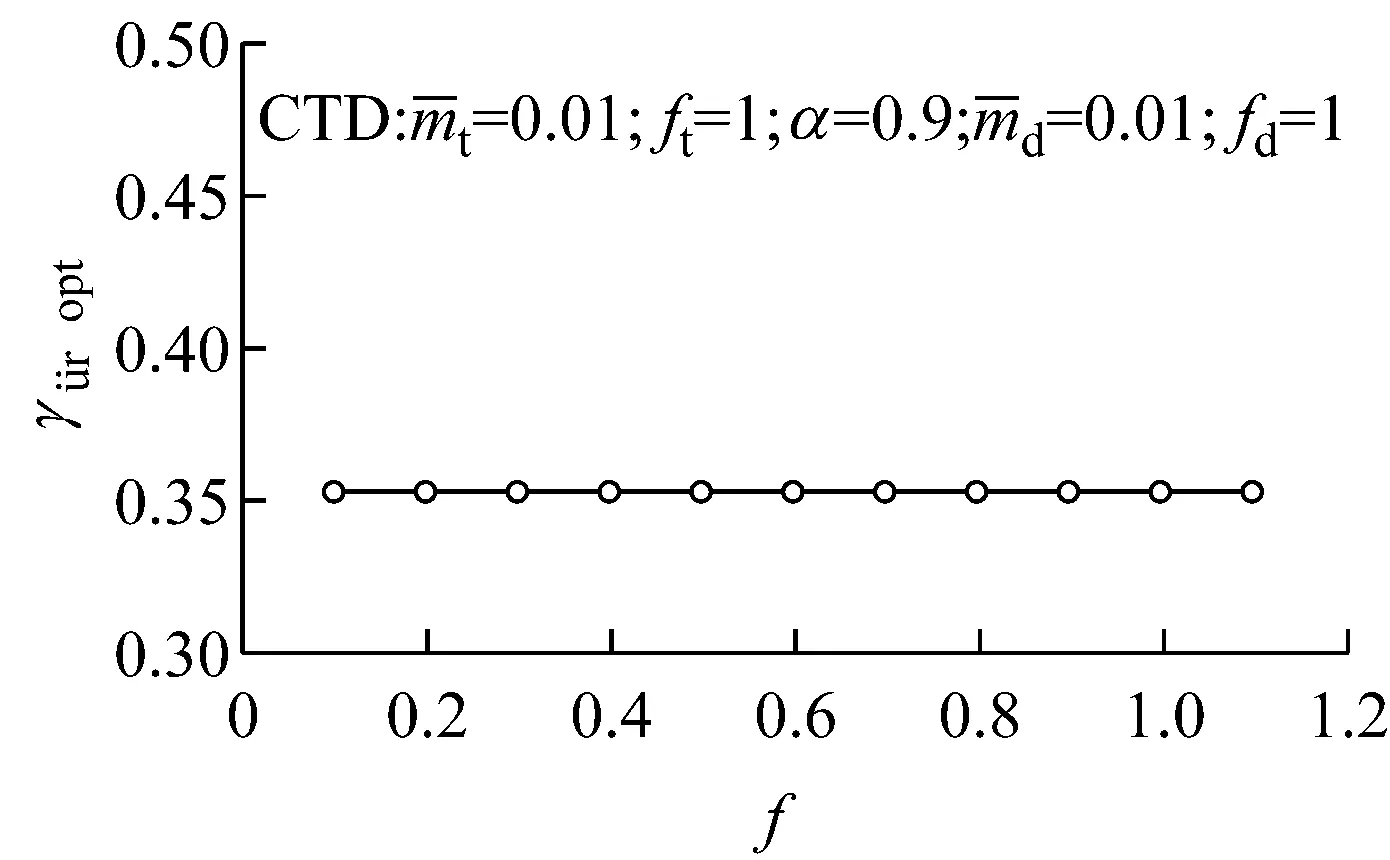
图16　CTD加速度协同损失因子

2.3CTD设置方法

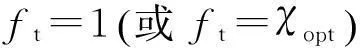
3结构风荷载随机响应计算

由于风荷载的随机过程特性，结构在风荷载下的响应可以利用其响应功率谱密度来描述，通过荷载的功率谱经过频响函数等方法求得.而对于可能存在的振型密集或具有非线性阻尼的随机振动分析，可采用虚拟激励法[6]计算.

结构顺风向振动是由脉动风引起的.一般可将脉动风用具有零均值的高斯平稳随机过程来表达.结构顺风向风荷载功率谱密度通常可采用Davenport谱和Harris谱等，考虑脉动风的相关性可获得结构顺风向风荷载谱.通过随机振动结果分析，便可获得结构响应的功率密度谱，进而可求得结构顺风向的均方差.随着建筑结构物高度不断增加，结构的横风向效应愈加明显，甚至会超过顺风向风载成为结构抗风设计的控制荷载[7].目前广泛采用基底高频测力天平进行相关研究，基于结构一阶振型为线性的假定求得结构的横风向气动力谱[7].同济大学全涌、顾明等采用高频测力天平技术拟合出了4种不同风场、15种不同外形的超高层建筑横风向力谱，并给出了闭合公式[8].与顺风向同理可得到横风向响应的均方差.对于某些外形变化较大的建筑在风载作用下还会产生扭转振动、结构的扭转振动是由于迎风和背风面及侧面风压的不对称所致，与紊流及尾流激励有关.当结构质点和刚度中心偏离时，弯曲振型与扭转振型出现耦合，结构响应与单一方向的响应有很大差别，表现为复杂的空间运动形式.因此这类建筑已考虑结构扭转效应的影响，其计算方法可参考文献[9].

采用CTD对超高层的风振进行控制时，由于CTD系统和主结构的耦合作用，结构动力方程中质量及刚度矩阵为非对称矩阵，阻尼矩阵也为非经典正交阻尼矩阵.对于这种问题，可采用文献[6]提出的虚拟激励法等进行解决.

4算例

某141层建筑功能为集商业、办公以及酒店为一体的综合性超高层建筑，结构高度为600 m，截面尺寸B=D=69 m，可根据文献[10]所示方法对原结构进行简化，原结构、简化后的质点串模型及相应的振动控制方案简图如图17所示.结构的阻尼比取为2%，当地的风环境为：C类地貌，10年一遇的基本风压w0为0.30 kPa.拟对结构舒适度性能进行评估，并对上文提及的三种阻尼器减振效果进行比较.

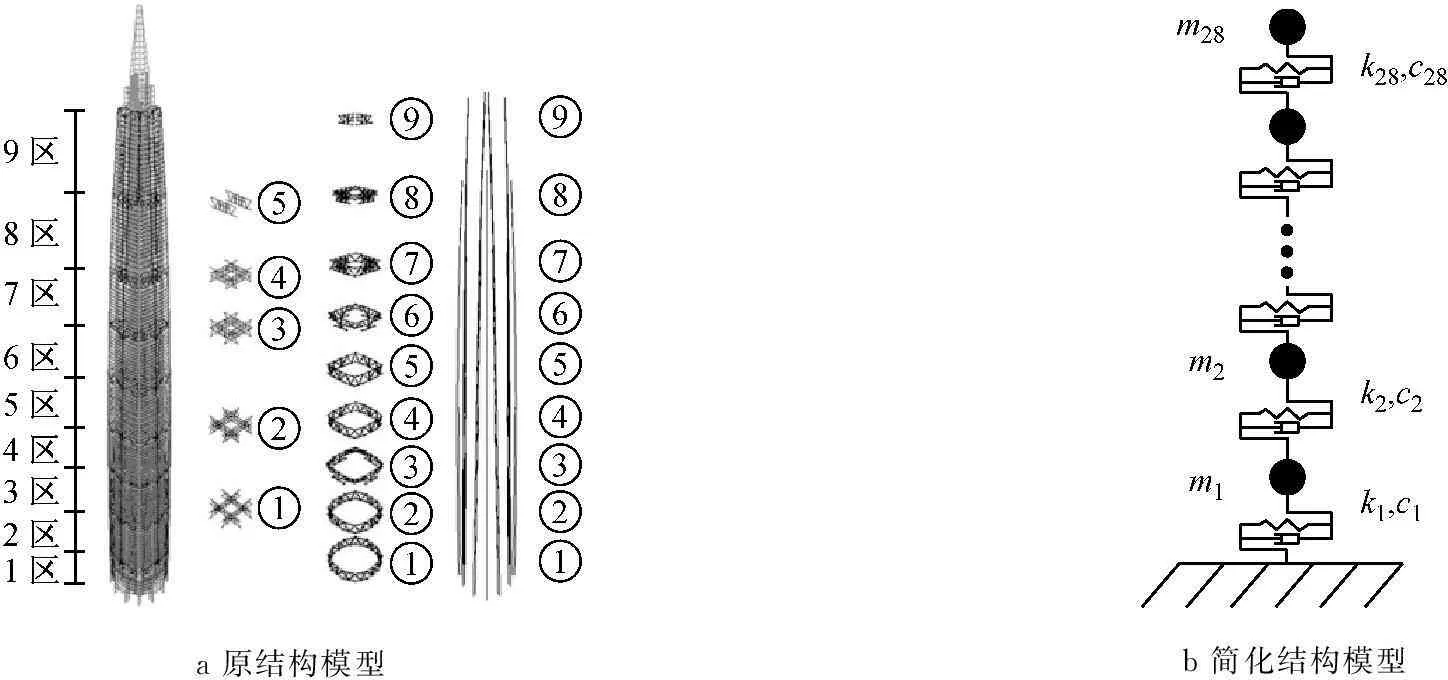
a原结构模型b简化结构模型

图17某超高层结构模型

Fig.17The model of a super tall building

4.1风载作用下结构响应求解

以10年一遇的基本风压0.3 kPa为例，其所对应的基本风速为21.91 ms-1.运用虚拟激励法求解结构响应，结构各质点的加速度响应标准差如图18～图19所示，可以看出，主体结构在横风向的响应要大于其顺风向响应.需要指出的是，在计算横风向结构响应时，由于采用的是基底高频测力天平的相关结果，其是基于建筑物1阶振型近似为线性的假设，得到作用在建筑物上的广义1阶力谱，因此其结构响应为在竖向上也表现为近似线性.而在顺风向计算时，考虑了所有参振振型，结构的1阶振型呈弯剪型.

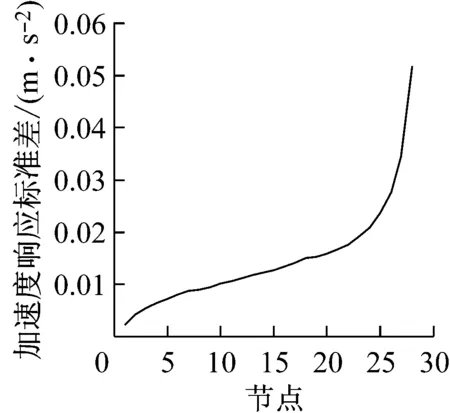
图18　结构顺风向加速度响应均方差

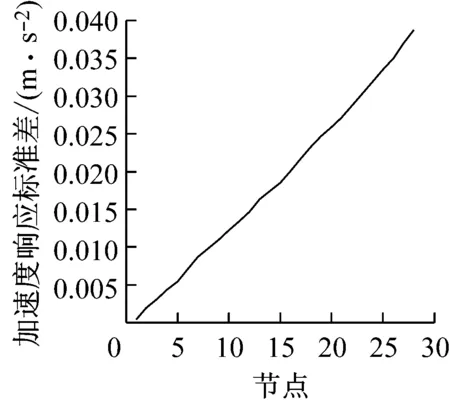
图19　结构横风向加速度响应均方差

4.2TMD和TLCD减振效果分析

合理布置阻尼器能够有效降低结构的响应加速度，进而提高结构的舒适度，阻尼器的作用效果可以通过减振系数表示.定义结构加速度响应均方差的减振系数η，如下：

(18)

由于该结构受横风向荷载控制，利用虚拟激励法求解结构在横风作用下的加速度响应，并进行数据处理得到TMD和TLCD的减振系数与参数的关系，如图20和图21所示.

4.3TMD,TLCD与CTD减振效果比较

设置各阻尼器的质量比均为0.01，具体参数为

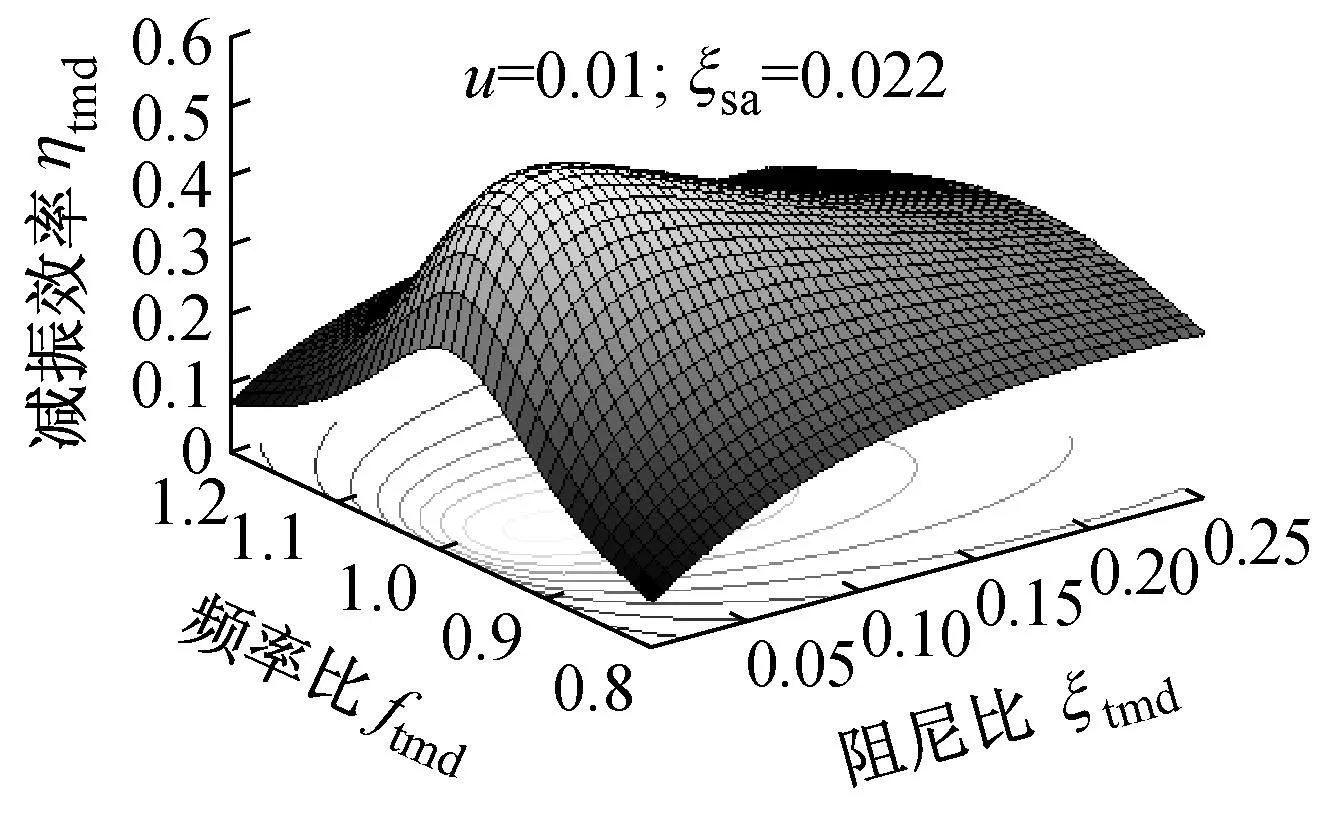
图20　TMD减振效率与频率比、阻尼比的关系

Fig.20Relationship amongst frequency ratio, damping ratio and vibration control efficiency of TMD

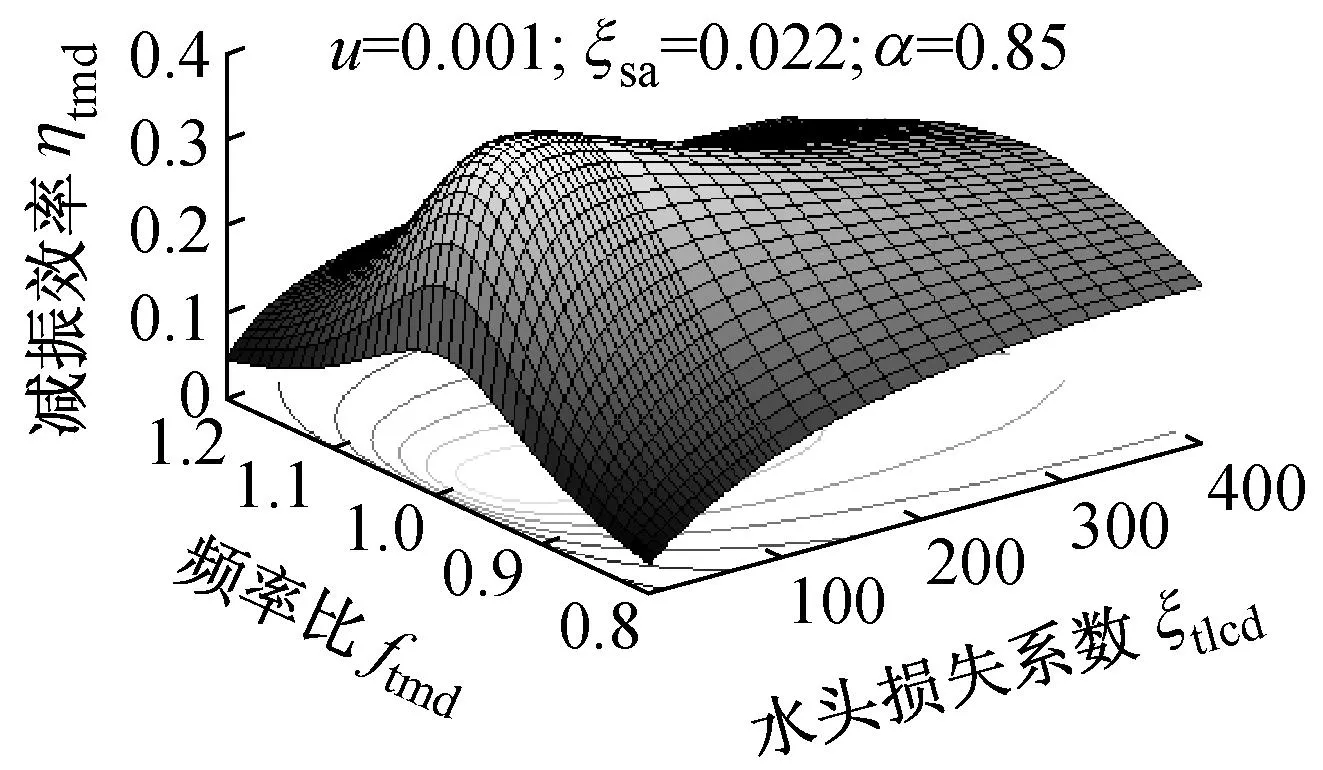
图21　TLCD减振效率与频率比、水头损失系数的关系

Fig.21Relationship amongst head loss coefficent, frequency ratio and vibration control efficiency of TLCD

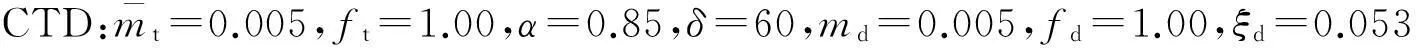
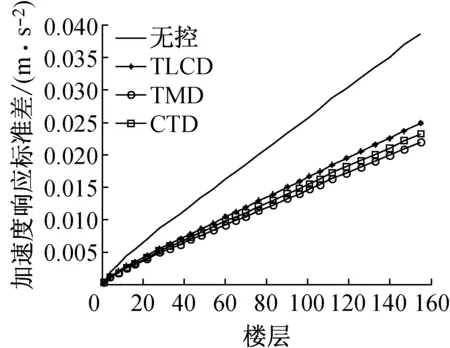
图22　结构各节点加速度响应标准差

5结论

通过对CTD的减振思想、工作原理及减振效率的分析，可得到以下结论：

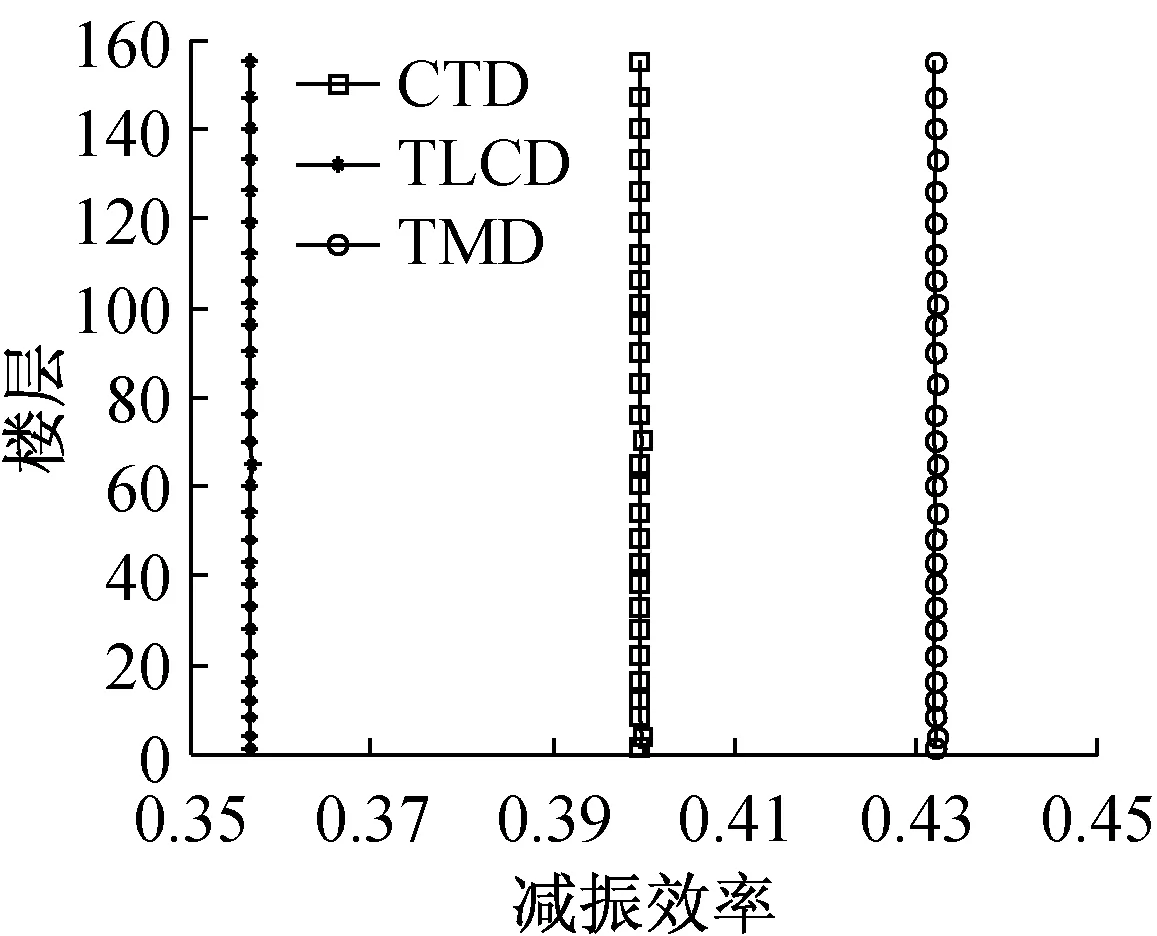
图23　CTD，TMD和TLCD减振效率比较

(1)CTD建立在充分结合利用TMD的高效性与TLCD的经济性的基础上；单质点案例最优参数配置下，质量比为0.02的CTD减振效率高达50%；超高层案例最优参数配置下，质量比为0.01的CTD减振效率可达40%；CTD的减振效率介于相同参数配置的TMD和TLCD之间，是一种极具竞争力的减振手段；

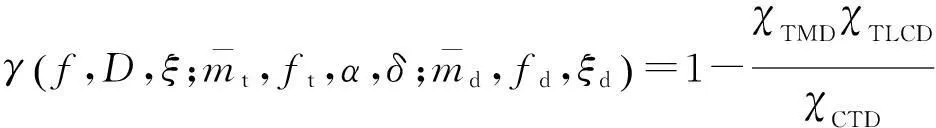
(3)CTD的参数设置应根据结构特点和舒适度目标要求进行，提出了CTD配置的一般方法.

参考文献:

[1]Soto M G, Adeli H. Tuned mass dampers[J]. Archives Computational Methods in Engineering, 2013， 20:419.

[2]Xu Y L, Samali B, Kwok K C S. Control of along-wind response of structures by mass and liquid dampers[J]. ASCE Journal of Engineering Mechanics, 1992, 118(1): 20.

[3]黄东阳.调谐类阻尼器的性能改良研究[D]. 哈尔滨：哈尔滨工业大学，2010.

HUANG Dongyang. Research on performance improvement of tuned typed dampers[D]. Harbin: Harbin Institute of Technology, 2010.

[4]兰文武.调频液体阻尼器对高层建筑结构地震反应控制效果的研究[D]. 广州：华南理工大学,1995.

LAN Wenwu. Study of earthquake-induced vibration control for tall buildings by tuned liquid damper[D]. Guangzhou: South China University of Technology, 1995.

[5]Balendra T, Wang C M, Cheong H F. Effectiveness of tuned liquid column dampers for vibration control of towers[J]. Engineering Structures, 1995, 17(9):668.

[6]林家浩, 张亚辉. 随机振动的虚拟激励法[M]. 北京：科学出版社，2004.

LIN Jiahao, ZHANG Yahui. Pseudo-excitation method for random vibration[M]. Beijing: Science Press, 2004.

[7]全涌, 曹会兰, 顾明. 高层建筑横风向风效应研究综述[J]. 同济大学学报: 自然科学版, 2010, 38(6): 810.

QUAN Yong, CAO Huilan, GU Ming. Cross-wind effect of high-rise buildings: state of art[J]. Journal of Tongji University: Natural Science, 2010, 38(6): 810.

[8]全涌, 顾明. 超高层建筑横风向气动力谱[J]. 同济大学学报: 自然科学版, 2002, 30(5): 627.

QUAN Yong, GU Ming. Power spectra of across-wind loads on super high-rise buildings[J]. Journal of Tongji University: Natural Science, 2002, 30(5): 627.

[9]唐意, 顾明, 金新阳. 偏心超高层建筑的风振研究[J]. 同济大学学报: 自然科学版, 2010, 38(2): 178.

TANG Yi, GU Ming, JIN Xinyang. Research on wind-induced response of structurally asymmetric tall buildings[J]. Journal of Tongji University: Natural Science, 2010, 38(2): 178.

[10]刘彬, 丁桦, 时忠民. 基于柔度修正的局部刚体化结构动力模型简化方法[J]. 工程力学, 2007, 24(10): 25.

LIU Bin, DING Hua, SHI Zhongmin. A model reduction method for dynamic analysis based on quasi-rigid-body mode and flexibility modification[J]. Engineering Mechanics, 2007, 24(10): 25.

[11]瞿伟廉, 陶牟华. 五种被动动力减振器对高层建筑脉动风振反应控制的实用设计方法[J]. 建筑结构学报，2004, 22(2): 29.

QU Weilian, TAO Muhua. Practical design method for effect of five kinds of passive dynamic absorbers on fluctuation wind-induced vibration response control of tall buildings[J]. Journal of Building Structures, 2004, 22(2): 29.

Combined Tuned Damper-based Wind-induced Vibration Control for Super Tall Buildings

ZHAO Xin1,2， WANG Lilin1, ZHENG Yimin1,2

(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. Tongji Architectural Design (Group) Co. Ltd., Shanghai 200092, China)

Abstract：To fully utilize the high efficiency of the tuned mass damper (TMD) and the economic advantage of the tuned liquid column damper (TLCD), a combined tuned damper (CTD) was proposed, and the wind-induced vibration mitigation effects of super tall buildings with such a combined tuned damper, were investigated. A kinematic equation was derived, which verified the feasibility of CTD theoretically. The collaborative loss coefficient was proposed to evaluate the performance loss due to the direct connection of TMD and TLCD to the structure of CTD. A comparative study was made of the vibration control efficiency of CTD with those of TMD and TLCD. The results show that the CTD with different parameters performs differently in vibration control and leads to different collaborative loss coefficients. The maximum collaborative loss coefficient can be up to 35%. With the same parameters, the vibration control of CTD is between those of TLCD and TMD, which makes CTD a competitive vibration control option.

Key words：super tall buildings; combined tuned damper; wind-induced vibration control; collaborative loss coefficient; tuned mass damper (TMD); tuned liquid column damper (TLCD)

文献标志码：A

中图分类号：TU973

基金项目：上海市优秀技术带头人计划(14XD1423900)； 上海市科技攻关计划(09dz1207704)

收稿日期：2014—12—17

第一作者： 赵昕(1975—)，男，高级工程师，工学博士，硕士生导师，主要研究方向为超高层建筑基于性能的优化设计.

E-mail:22zx@tjadri.com