弹形变化对超音速下弹丸气动特性的影响
2016-05-28沈思颖陈川琳吴志林
沈思颖,陈川琳,吴志林
(南京理工大学 机械工程学院,南京 210094)
弹形变化对超音速下弹丸气动特性的影响
沈思颖,陈川琳,吴志林
(南京理工大学 机械工程学院,南京210094)
摘要:通过建立小口径弹丸三维模型,采用混合网格划分方法,运用工程流体软件进行了弹丸外流场数值仿真,并对仿真计算的准确性进行了验证。以某5.8 mm枪弹为基础,改变弹丸外形,弧形部和尾锥部尺寸,计算得到弹丸超音速飞行状态下不同气动力参数,研究弹形变化对其气动特性的影响规律,结果表明:弹形各部分尺寸变化对气动力影响不同,弧形部较尾锥部影响更加明显,而尾锥长度比尾锥角的影响更大。
关键词:弹丸;混合网格;弹形变化;气动特性
对于弹箭空气动力特性的研究,随着计算机的发展,采用数值模拟方法结合风洞试验,优势明显,现已广泛应用于流体计算领域的各行各业。网格划分是数值仿真中的关键,合理选择网格对于节约计算时间、提高计算精度事半功倍。本文采用了特点鲜明、运用成熟的混合网格划分方法[1-2],并通过已有弹种的仿真计算与有关文献[3]数据进行了对比验证,证实该方法可适用于弹丸无旋状态的流场模拟。
枪弹方案设计中最重要的是外形设计,不同的外形尺寸对气动力特性、弹道性能、飞行稳定性以及射击精度的影响各不相同。郭玉洁等研究了偏转头弹箭的流场特性[3],认为其主要表现为头部激波变化;张国伟等则对某钝头子弹的气动特性进行研究[4];吴振宇、崔新军分析了某超音速火炮弹丸尾部和底部流动,提出了确定最佳尾锥角的计算方法[5-6];王乐等仿真计算了底部凹陷对气动特性的影响[7]。然而相关研究中,对小口径枪弹领域涉及甚少。Paul Weinacht,Sidra I.Silton等通过仿真计算研究了具有表面膛线刻痕的小口径弹丸在不同飞行状态下气动特性,得出了刻痕对气动力影响很小等结论[8-9]。本文在混合网格划分的基础上,针对国内某5.8 mm小口径枪弹,提出合理假设,改变弹丸外形,主要是弧形部及尾锥部尺寸的改变,通过FLUENT对弹丸外流场进行数值仿真,获取其无旋状态飞行的空气动力参数,研究超音速下气动特性随弹形的变化规律。
1数值模拟方法
1.1网格划分
本文采用GAMBIT软件生成弹丸表面网格,TGRID软件生成混合网格。
图1为静态弹丸附近流场的计算网格示意图。为了更好捕捉壁面湍流细节,本研究采用棱柱网格构成边界层。取壁面y+值为1,第一层边界层厚度约为4×10-7m,边界层层数为20。流场其他区域由非结构网格填充,边界层网格沿壁面法向增长率为1.15,实现流场内网格尺寸的平滑过渡。整个流场为长600 mm,半径150 mm的计算域,网格数量约为290万。

图1 静态网格示意图
1.2控制方程
计算采用三维可压流的雷诺平均N-S方程[10]
其中:V为控制体;S为控制边界;W为守恒变量;F(W)为对流通量;Fv为黏性通量。
1.3求解方法
选择Realizablek-ε湍流模型,在壁面附近区域采用增强型壁面方法处理[11],其模拟结果更符合真实情况。对于高速可压缩理想气体,选用密度基有限体积、二阶迎风格式的离散方法、三系数Sutherland定律计算黏性,对流通量采用Roe-FDS通量差分方法。
1.4边界条件
无限远处采用压力远场边界条件。弹体采用Stationary Wall固定壁面边界。
2计算验证
选取国外5.56 mm M193弹丸进行计算验证,计算了弹丸在4个马赫数、2个攻角下的气动力系数。图2为各气动力系数随马赫数变化的情况。
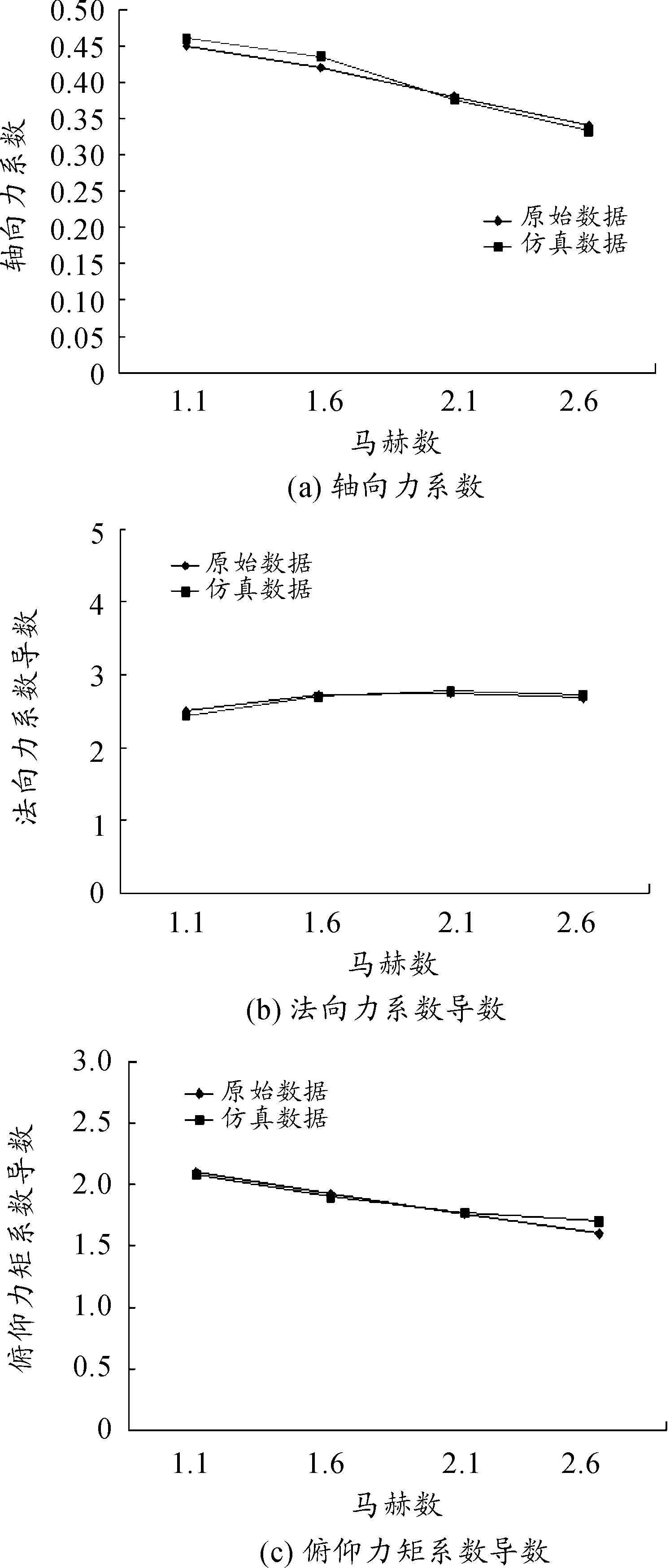
图2 气动力系数随马赫数变化的情况
计算结果表明,各气动力系数与文献[3]中结果误差均在10%以内甚至更小,满足误差要求范围,其变化趋势与文献[3]一致,表明该计算方法是准确合理的。
3弹形变化对气动特性的影响
选取国内某5.8 mm口径枪弹为对象(图3),来流为2.2马赫数,弹丸攻角为0°和2°。计算阻力、升力和静力距3个气动力系数,研究弹形变化对超音速下弹丸气动特性的影响。

图3 弹丸外形示意图
3.1基本假设
本研究提出弹丸外形改动的3个基本假设:
1) 弹药设计基本原则:弹丸全长是在弹丸质量确定后确定的,即弹长不变;
2) 控制变量原则:研究单一变量尺寸时,其他尺寸保持不变。质心位置始终不变;
3) 合理性原则:尺寸变化在弹丸外形设计的合理范围内。
另外,现有设计经验认为圆柱部主要起到弹丸在膛内运动的导引作用,保证膛内稳定,其导引性对弹丸出膛口的初始扰动密切相关,对弹丸气动特性影响不大,因此不考虑其他变量引起的圆柱部长度变化对气动的影响;对于该弹丸,尖部过渡圆角半径随圆弧的变化很小,影响很小,故未作考虑。
3.2结果分析
由于各气动系数量级不同,将改变尺寸后各弹形的计算结果与标准弹形的结果比较,得出各气动系数随尺寸的变化率。
3.2.1弧形部尺寸变化的影响
图4给出了气动系数随弧形部长度变化的计算结果。随着弧形部长度增加,各力和力矩系数减小,其中俯仰力矩系数的变化幅度最为明显。
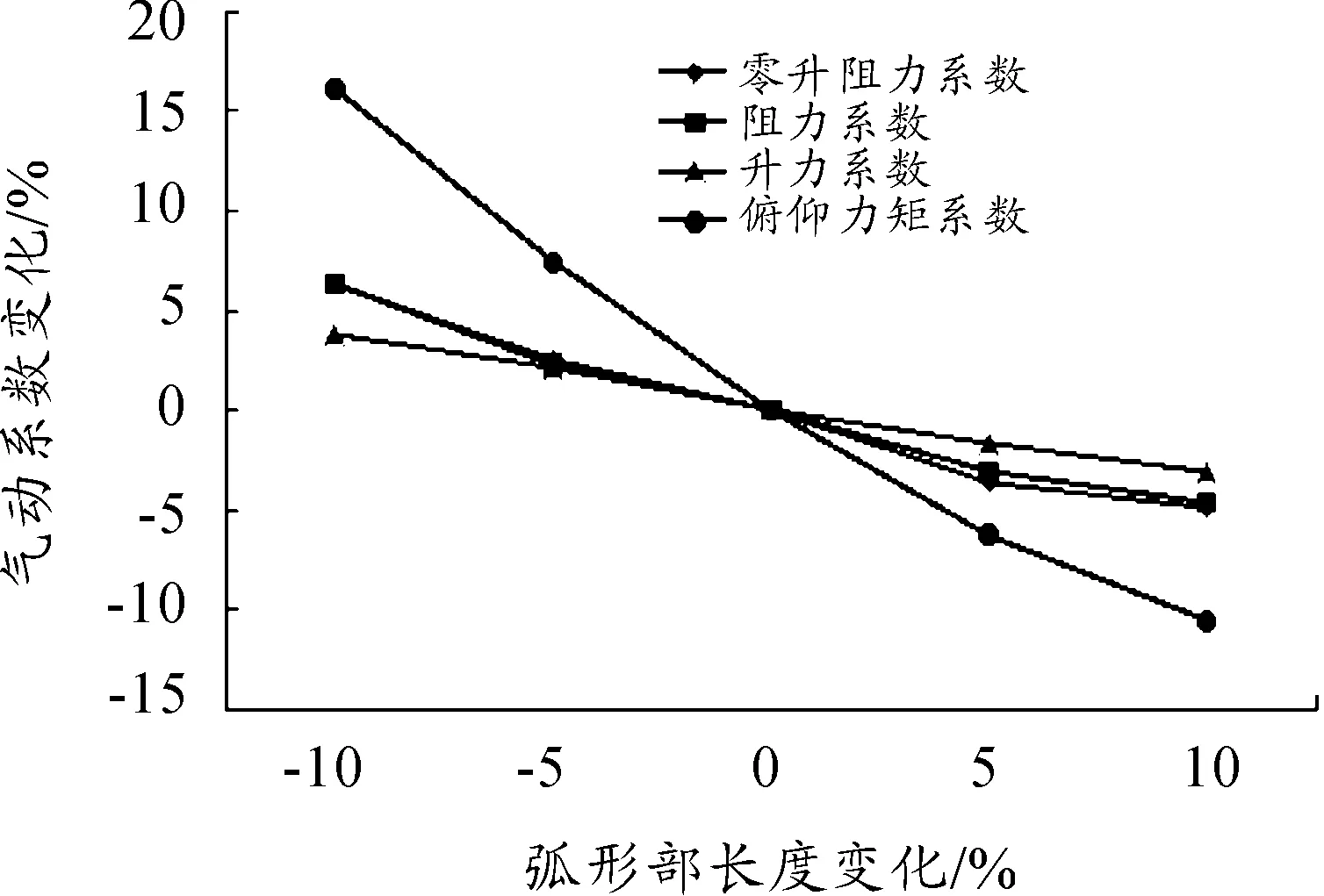
图4 气动系数随弧形部长度变化的情况
图5为0°攻角时不同弧形部长度的两弹丸剖面压力云图与叠加情况。从图5看出,由于弹尖部尺寸没变,弧形部长的弹丸更尖锐,弧形更平缓,弹头波越往后越弯曲,激波角变小,激波强度减小,波阻减小。同时,气流改变了速度大小和方向,此处相当于攻角减小,升力将减小,升力系数减小;反之弧形变陡,升力系数增大。尾部压力轮廓线几乎重叠,弹尾波相同。
图6比较了有攻角时长短不同的两个弧形部剖面压力云图。可看出弧形部短的弹头下方压力明显高于弧形部长的弹头。
升力系数减小,其绕质心的力矩减小,导致俯仰力矩系数减小。根据高巴尔经验公式,弧形部变长,压心后移,压心质心距变短,俯仰力矩减小。
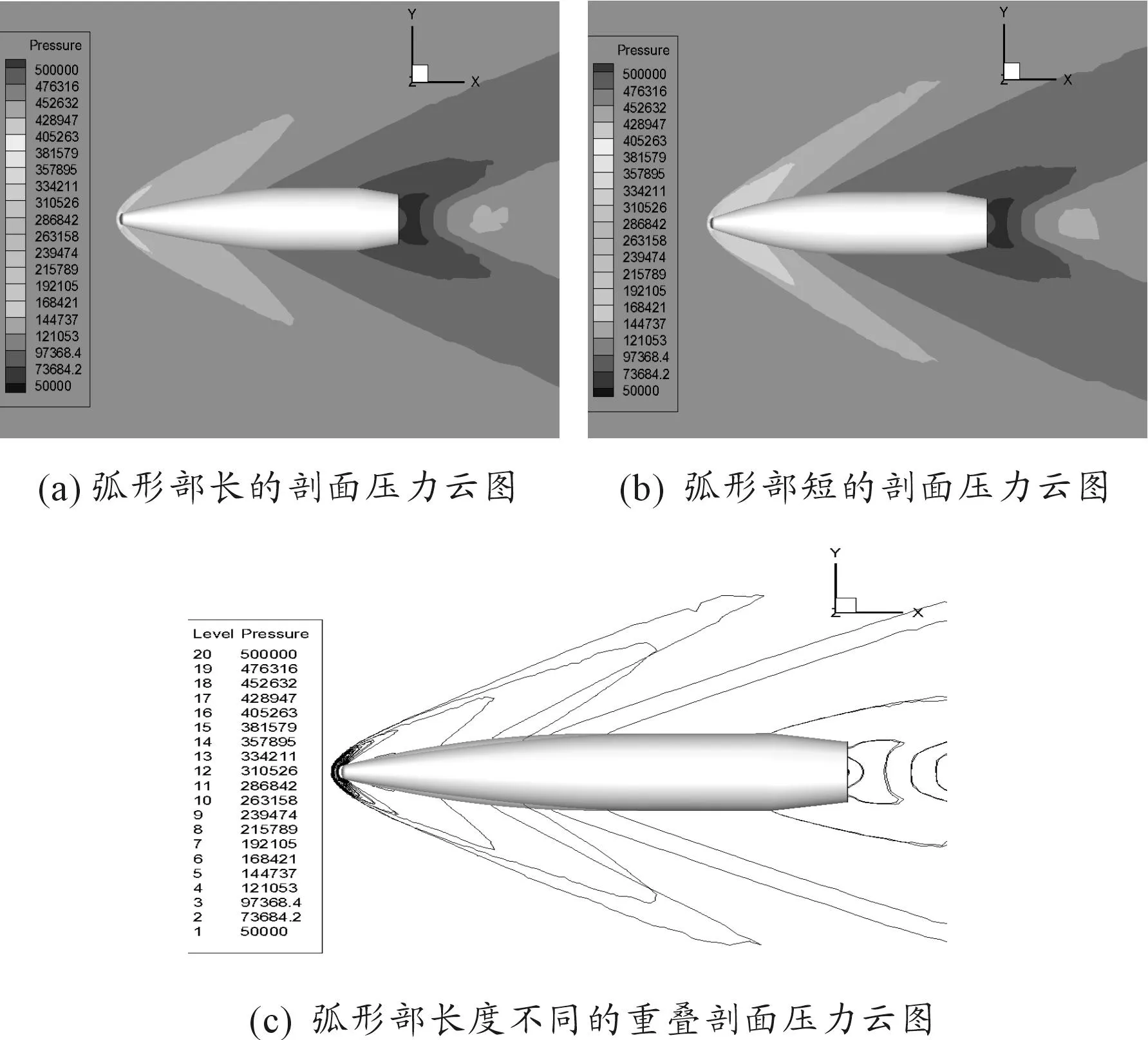
图5 0°攻角时不同弧形部长度的剖面压力云图
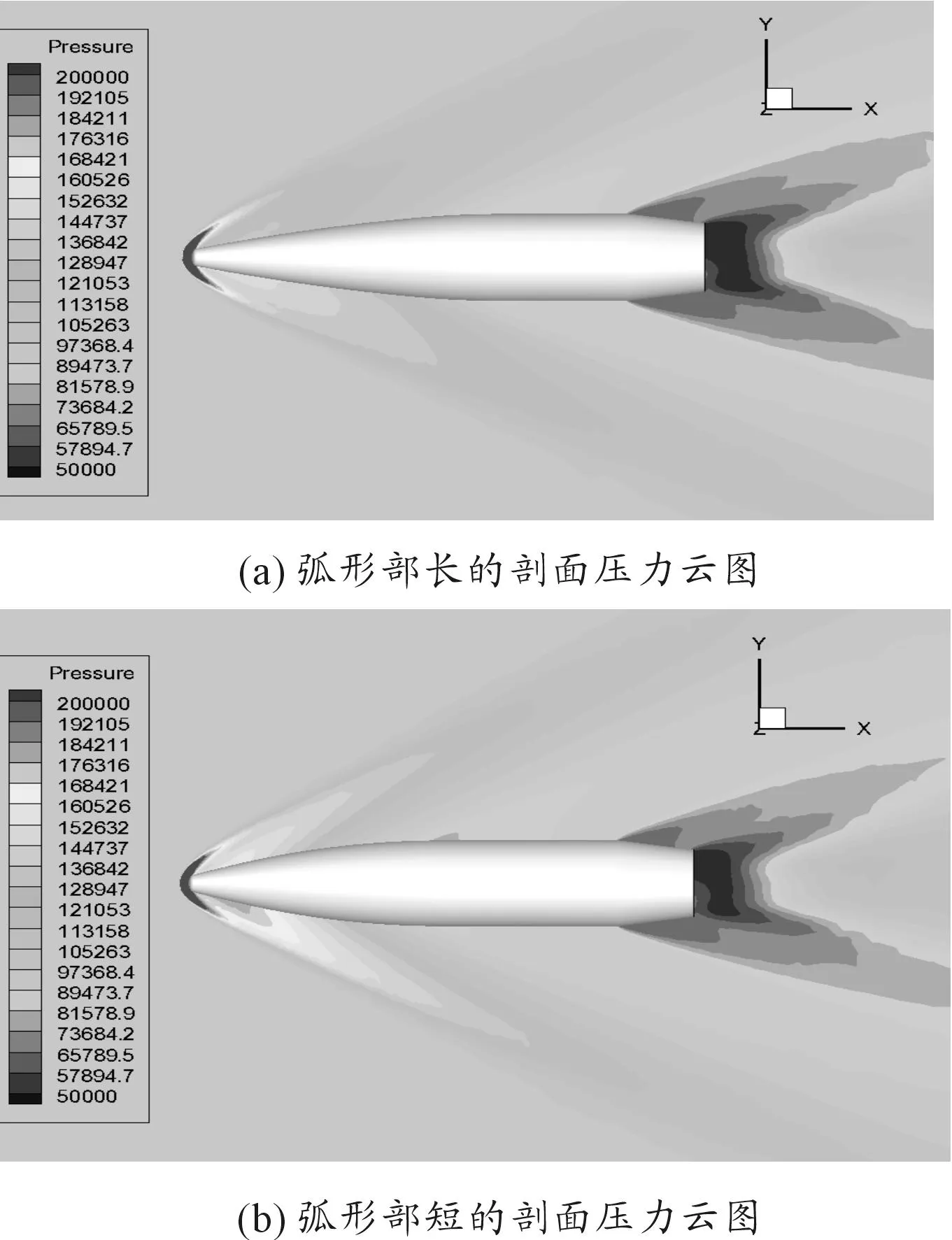
图6 2°攻角时不同弧形部长度的剖面压力云图
通过改变弧形部母线半径和尖部尺寸,使弹头变得钝化或尖锐。图7为气动系数随弧形部母线半径变化的计算结果。表明母线半径越小,弹头越锐,阻力系数越小,升力系数呈增大趋势;而俯仰力矩系数减小更加明显。

图7 气动系数随弧形部母线半径变化的情况
图8为0°攻角时两不同母线弹丸的剖面云图及叠加情况。由图可看出弹头变钝,激波角增大,激波面更宽,对空气扰动增强,弹头激波增强,消耗动能多,波阻增大,总的阻力系数增大;反之波阻减小,总的阻力系数减小。尾部压力轮廓线几乎重叠,弹尾波相同。而图9则比较了有攻角时不同母线的弹丸压力云图。由图可看出弹头锐的弹丸,激波锥角小,越贴近弹头表面,下方的高压区也越贴近表面,容易造成上下压差增大,升力增加,升力系数增大。

图8 0°攻角时不同弧形母线的剖面压力云图
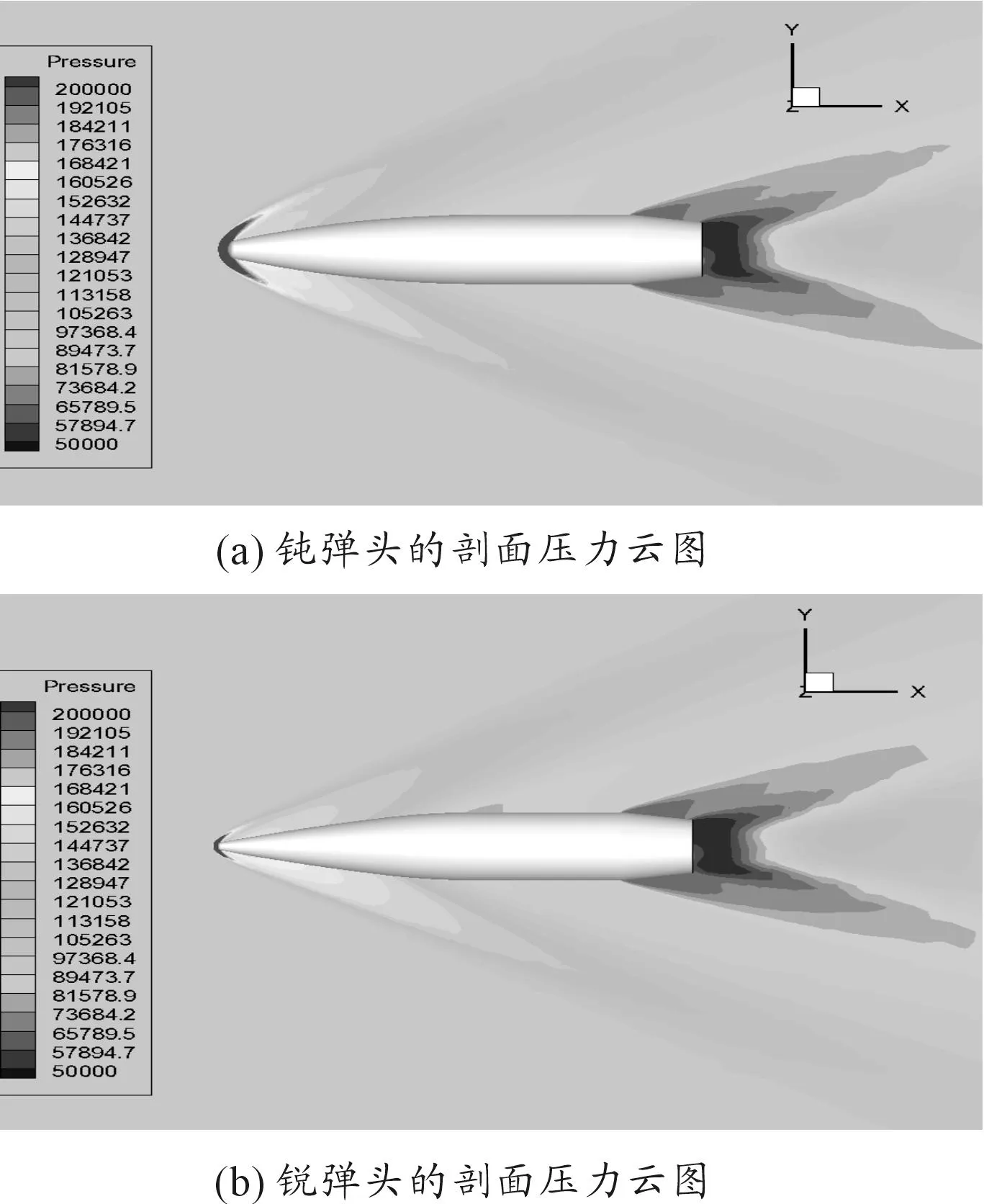
图9 2°攻角时不同弧形母线的剖面压力云图
弹尖空气流动平缓,附面层未分离,不易产生低压区,也就没有产生新的压差,所以弹头变钝后升力系数没什么变化;如果弹头变尖锐超过一定程度后,弹尖处背风面附面层容易出现一定程度的分离,压力降低形成低压区,上下表面产生新的压力差,升力增加,俯仰力矩增大。弹头钝,压心前移,升力增大,所以俯仰力矩增大;弹头锐,压心后移,翻转力臂减小,升力增大。表1为压心及压心后移距离计算结果。

表1 压心位置变化及计算结果
从结果可知,压心质心距缩短10.13%,较图7中升力系数增加(约5%)幅度大,所以俯仰力矩系数减小。可见弧形部母线曲率半径的改变对压心位置影响明显。
3.2.2尾锥部尺寸变化的影响
图10为气动系数随尾锥长度变化的情况。随着尾锥变长,阻力系数变小,升力系数变小,俯仰力矩系数变大。其原因是:尾锥越长,导致弹底直径越小,底面积减小,底部低压区变小,底阻减小,弹丸阻力系数减小。图11比较了不同尾锥长度的剖面压力云图,也可发现两个弹丸底部压力颜色明显不同。
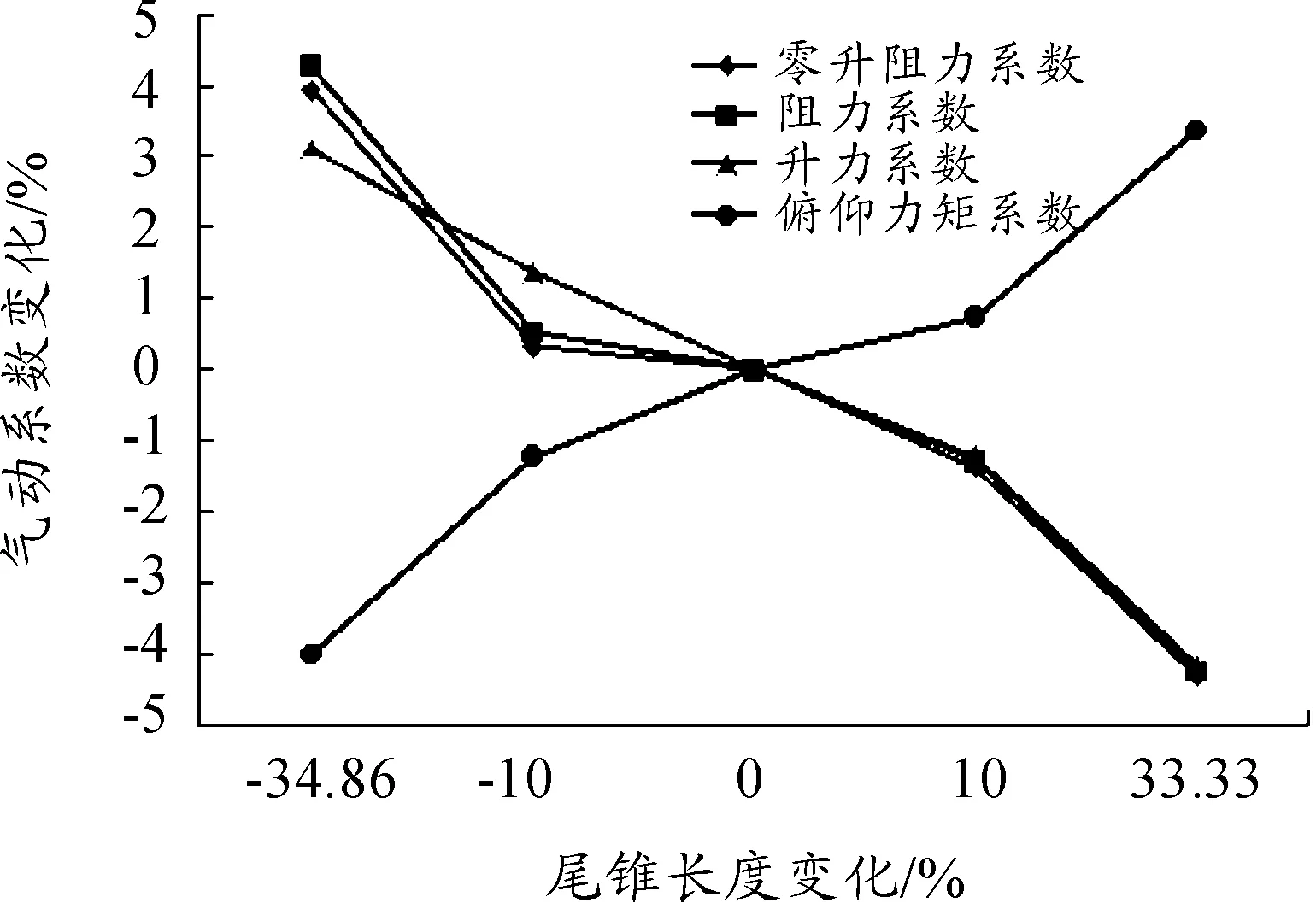
图10 气动系数随尾锥长度变化的情况
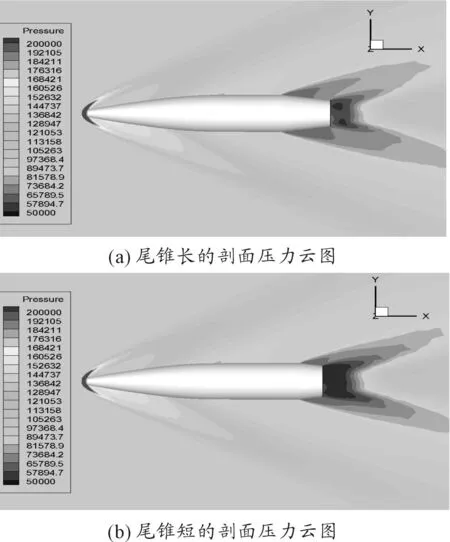
图11 2°攻角时不同尾锥长度的剖面压力云图
尾锥变长,弹尾部总体受力面积变大,向下的压力增大,所以总升力系数减小。而尾锥向下的压力增大,其绕质心的力矩使弹轴向增大攻角的方向转动,总的俯仰力矩增大。反之减小。
图12为锥角变化引起的气动系数变化结果。随着尾锥角变大,阻力系数先下降,到最低点后升高;升力系数减小,俯仰力矩系数增大。从图13不同锥角的压力云图比较看出,尾锥角变大,导致弹底直径减小,底面积减小,底部低压区变小,底阻减小,同时尾锥角变大引起尾部拐角处的初始膨胀角增大,膨胀波增强,波阻增大,此时,底阻和尾部波阻共同影响阻力大小,存在一个最佳尾锥角使阻力最小。数据显示该弹的最佳尾锥角应该就在增幅10%的角度附近。

图12 气动系数随尾锥角变化的情况

图13 2°攻角时不同尾锥角的剖面压力云图
尾锥角变大,弹尾部总体受力面积变大,向下的压力增大,升力系数减小,俯仰力矩系数增大;反之升力系数增大,俯仰力矩系数减小。综合前文尾锥长度变化影响的分析,可得出规律:尾锥部分引起的俯仰力矩系数变化必然与升力系数变化相反。
表2为底部直径相同情况下的气动系数对比数据。可知底部直径相同时,尾锥角大的阻力大,尾锥长的阻力小。由于波阻主要与尾锥角大小相关,因此尾锥角大的,波阻较大,阻力系数较大;而尾锥长的,锥角相对较小,波阻较小,阻力系数较小;同理,尾锥短的阻力系数大,尾锥角小的阻力系数小。又根据前文尾锥形状尺寸与升力系数的影响分析,尾锥长的,尾锥角较小,升力系数较小,俯仰力矩系数较大;尾锥角大的,尾锥较短,升力系数较大,俯仰力矩系数较小。

表2 底部直径相同的气动系数对比 %
4结论
本研究采用混合网格划分方法,用FLUENT软件模拟了弹丸流场,通过已有数据计算验证,计算结果误差满足要求,表明该数值模拟方法准确合理,可运用于常规枪弹仿真。采用该方法,计算了国内某5.8mm小口径枪弹的静态各气动力参数,研究了弹形变化对超音速下弹丸气动特性的影响,分析产生原因。通过本文研究,得到了如下结论:弧形部尺寸对阻力和升力系数影响较大,对力矩系数的影响比对力系数的影响大;尾锥尺寸对气动系数的影响较小,其中长度的影响比锥角的影响大;弧形部尺寸对整个气动系数的影响大于尾锥部尺寸的影响。该研究有助于枪弹外形的理论设计,具有一定参考价值。
参考文献:
[1]郑冠男,邓守春,韩同来,等.基于混合网格Navier-Stokes方程的并行隐式计算方法研究[J].应用力学学报,2011,28(3):211-219.
[2]曹建.适应复杂外形粘性流动模拟的混合网格生成算法[D].杭州:浙江大学,2013.
[3]SIDRA I S,PAUL W.Effect of Rifling Grooves on the Performance of Small-Caliber Ammunition[Z].ADM002187,
2008.
[4]郭玉洁,陈志华,刘志明.偏转头弹箭流场特性研究[J].四川兵工学报,2013,34(4):29-32.
[5]张国伟,张宇,梁永直.钝头子弹气动特性分析[J].弹箭与制导学报,2006,26(2):91-93.
[6]吴振宇,崔新军.超音速弹丸最佳尾锥角的确定[J].弹道学报,1996,8(2):23-27.
[7]吴振宇,崔新军.弹丸初步设计中尾锥角的选取方法[J].兵工学报,1998,19(1):90-92.
[8]王乐,宋卫东,杨晓霖.底部凹陷对弹丸气动特性的影响[J].计算机仿真,2013,30(1):70-73.
[9]PAUL W.Validation and prediction of the Effect of Rifling Grooves on Small-Caliber Ammunition Performance[Z].AIAA-2006-6010,2006.
[10]SIDRA I S,DAVID W W.Experimental Determination of the Effect of Rifling Grooves on the Aerodynamics of Small Caliber Projectiles[Z].AIAA-2006-6009,2006.
[11]蒋胜矩,刘玉琴,党明利.基于定常NS方程的飞行器滚转阻尼力矩系数导数计算方法[J].弹箭与制导学报,2008,28(1):180-182.
[12]王福军.计算流体动力学分析—CFD软件原理与应用[M].北京:清华大学出版社,2004.
[13]舒敬荣, 张继春, 常思江. 空气动力非对称弹丸大攻角旋转共振运动研究及应用[J].兵工学报,2014(4):441-447.
(责任编辑周江川)
本文引用格式:沈思颖,陈川琳,吴志林.弹形变化对超音速下弹丸气动特性的影响[J].兵器装备工程学报,2016(4):15-19.
Citation format:SHEN Si-ying, CHEN Chuan-lin, WU Zhi-lin.Bullet-Shape Change on Effect of Aerodynamic Characteristics of Supersonic Projectile[J].Journal of Ordnance Equipment Engineering,2016(4):15-19.
Bullet-Shape Change on Effect of Aerodynamic Characteristics of Supersonic Projectile
SHEN Si-ying, CHEN Chuan-lin, WU Zhi-lin
(School of Mechanical Engineering, Nanjing University of Science & Technology, Nanjing 210094, China)
Abstract:The projectile exterior flow field was simulated by fluid software through the establishment of three dimensional models of small caliber projectile and the hybrid grid method, and the accuracy of simulation was verified. Based on a 5.8 mm bullet, the projectile shape including arc and tail cone size were changed, and the different aerodynamic parameters of projectile flying in supersonic irrotational condition were got. Some effect laws about aerodynamic characteristics caused by bullet-shape change were studied. The results show that the effects of bullet size change on the aerodynamic are different, and the effect of arc is more obvious than that of tail cone and the effect of tail cone length is greater than that of tail cone angle.
Key words:projectile; hybrid grid; bullet-shape change; aerodynamic characteristic
文章编号:1006-0707(2016)04-0015-06
中图分类号:TJ011.+2
文献标识码:A
doi:10.11809/scbgxb2016.04.005
作者简介:沈思颖(1991—),男,硕士研究生,主要从事空气动力学研究。
收稿日期:2015-10-15;修回日期:2015-11-16
【装备理论与装备技术】
