稀疏线性预测字典在语音压缩感知中的应用

游寒旭, 李　为, 李　昕, 朱　杰

(上海交通大学 电子信息与电气工程学院,上海 200240)



稀疏线性预测字典在语音压缩感知中的应用

游寒旭, 李为, 李昕, 朱杰

(上海交通大学 电子信息与电气工程学院,上海 200240)

摘要:压缩感知理论框架可以同时实现信号的采样和压缩,将压缩感知应用于语音信号处理是近年来的研究热点之一.本文根据语音信号的特点,采用K-SVD算法获得稀疏线性预测字典,作为语音信号的稀疏变换矩阵.高斯随机矩阵用于原语音信号的采样从而实现信号的压缩,最后通过正交匹配追踪算法(OMP)和采样压缩匹配追踪算法(CoSaMP)将已采样压缩的语音信号进行信号重构.实验考察了待处理语音信号帧的长度、压缩比,稀疏变换字典以及压缩感知重构算法等因素对语音压缩感知重构性能的影响,结果表明,基于数据集训练的稀疏线性预测字典相比传统解析构造的离散余弦变换字典,对语音的重构性能具有0.6 dB左右的提升.

关键词:压缩感知; 语音信号处理; K-SVD; 稀疏线性预测字典

0引言

Nyquist采样定理要求传统语音信号处理系统的采样率至少是原始信号频率的2倍或以上以保证不失真地重构原始信号.对于传统语音压缩来说,语音首先经过高速采样,然后再采用传统的压缩算法对语音进行压缩处理,这一过程占据了大量的中间采样和存储资源.压缩感知(CS)理论由Donoho、Candes和Tao等[1-3]提出,旨在改变先采样后压缩的传统处理框架,让系统同时完成信号的采样和压缩.CS理论指出,当信号具有稀疏性或可压缩性时,可以通过最少的观测数来采样信号以保证信号的准确重构.这样一方面节约了采样和压缩成本,另一方面又达到了信号的采样和压缩同时完成的目的.CS理论“采样即压缩”的特性使得其应用研究涉及到了国内外语音信号处理的众多领域,如语音编码、语音识别、说话人识别、语音增强、音乐检索等等[4].

信号的稀疏性或可压缩性是CS理论的前提和必要条件,信号的稀疏性保证了仅仅利用少量的观测值就可以实现信号的准确重构而不丢失原信号的主要信息.CS理论指出,信号在稀疏基(字典)下的表示系数越稀疏则信号的重构质量越好,而语音信号稀疏分解算法将直接影响信号的稀疏性.Kassim等[5]把CS理论应用于低比特率语音编码,采用FFT,DCT和小波变换分别对语音信号进行稀疏分解;Zhang等[6]采用了DCT结合小波包的方式(DCWPT)来完成语音信号的稀疏分解,并对信号进行压缩感知处理和重构.DCT变换、FFT变换以及小波变换都是基于传统的解析方法,这类变换字典构造简单,但其原子不够丰富,而通过训练语音数据集学习来的过完备字典与解析构造的字典相比,原子的种类和数量更多,对待处理信号进行稀疏分解更有针对性.诸如MOD算法、K-SVD算法、ADMM算法等字典学习算法作为主流的学习算法[7],是稀疏分解领域重要的研究方向.Giacobell等[8]将预测系数求解从最小均方误差约束条件改为稀疏性约束条件,进而提出利用语音帧的线性预测信号与原信号之间残差的稀疏性来实现信号的稀疏分解.孙林慧等[9]则采用稀疏线性预测系数来构造线性预测字典,通过大量训练集并结合LBG聚类算法,构造更符合实用要求的过完备字典.李洋等[10]则采用K-SVD算法作为语音稀疏字典的学习算法,并结合压缩感知技术将之应用于语声恢复领域.

本文作者主要考察通过语音训练集来构造稀疏分解字典,从稀疏线性预测系数出发,采用K-SVD算法对语音训练集进行学习,构造稀疏线性预测字典(SLPD),用于语音信号的稀疏分解.首先通过分析语音线性预测系数的原理,利用语音信号帧的帧间相关性及预测残差的稀疏性,得到初始化线性预测字典,然后将之用于K-SVD算法的训练学习.另一方面,K-SVD算法字典的更新策略在字典训练过程中逐步地替换掉不符合要求的原子,直到字典能够达到误差和稀疏性要求为止,保证了语音信号稀疏分解的性能.与传统方法相比,本文作者构造的稀疏线性预测矩阵对语音信号更具有针对性.随着K-SVD算法不断的改进,本文作者提出的联合线性预测系数和K-SVD算法构造的稀疏分解字典也具有一定可扩展性.

文章内容安排如下:第1节首先介绍了CS理论的基本理论框架;第2节研究了采用K-SVD学习算法构造SLPD的方法;第3节通过实验来分析CS技术在语音信号处理的应用并分析了各因素对语音压缩感知性能的影响;最后对全文进行了总结,给出了结论.

1CS理论

为了缓解信号处理过程中由Nyquist采样率带来的采样和存储压力,Donoho等人提出了基于信号稀疏性的CS理论.这是一种新的信号描述和处理的理论框架,CS理论用远低于Nyquist采样定理要求的速率采样信号并完成压缩,信号的稀疏性和相应的重构算法保证了重构信号的准确性而不损失重要信息.

1.1基本原理

考虑信号x∈N×1表示一个N×1维列向量x=[x1,x2,…,xN]T,稀疏字典用D=[d1,d2,…,dL]表示,其中di=[d1,d2,…dN]T(i=1,2,…,L)为字典中的原子,L是字典长度.信号x可以用字典D中原子的线性组合来表示,即:

(1)

如果信号x是K稀疏的,那么根据压缩感知理论,采用一个与D不相关的观测矩阵Φ∈M×L对信号进行观测采样,其中K≤M≪N,得到一个M×1维的被观测信号y∈M×1,即:

(2)

其中Θ=ΦD.这里,采样过程是非自适应的,也就是说,Φ无须根据信号s而变化,观测不再是信号的点采样而是更一般的K线性泛函.由于M≪N,这就使得采样的同时也达到了压缩的目的,压缩比为M/N.

1.2信号重构

信号的重构就是从压缩观测信号y中恢复出原信号x.由于M远小于N,求解式(2)就成了一个解欠定方程组的问题.考虑到有限等距性质(RIP)保证了观测矩阵不会把两个不同的K稀疏信号映射到同一个集合中(保证原空间到稀疏空间的一一映射关系),CS理论证明[1],当Θ满足RIP并且s是稀疏的,那么s的求解可以转化为一个L1范数优化问题,它与L0范数优化问题具有同等的解,且是唯一解.即

(3)

L1范数优化问题是一个凸优化问题,可以方便地化简为线性规划问题.目前针对信号的重构,国内外学者已提出许多重构算法[11],主要包括贪婪追踪类算法,凸松弛算法,还有要求对原始信号具有少量先验知识的基于统计性算法.采用正交匹配追踪(OMP)算法和压缩采样匹配追踪(CoSaMP)算法来对语音信号进行重构.

2稀疏线性预测字典

如上所述,用于信号稀疏分解的字典通常分为两种:基于解析方法构造的字典以及基于训练样本的字典.孙林慧在文献[9]中指出,常用的基于解析方法构造的字典如DCT或DWT在低压缩比的情况下,语音信号的重构效果不够好.本文作者利用语音信号的线性预测信号与原信号的误差的冗余性,通过线性预测系数(LPC)来构造稀疏字典,提高语音信号帧的稀疏性.

2.1线性预测系数矩阵

语音信号处理理论证明,语音信号帧的各个值在某种准则条件下(如MMSE)可以由过去的若干值线性表示.假设一个长度为N的语音帧为x=[x1,x2,…,xN]T,则语音值xn(n=1,2,…,N)的p阶线性预测值为:

(4)

其中p是预测阶数,ai是线性预测系数.原信号与预测信号的误差称为稀疏冗余,由下式给出:

(5)

其中a0=1.式(5)的矩阵形式可以表示为:s=A-1x,其中s=[s1,s2,…,sN]T,A-1是线性预测系数矩阵:

(6)

信号x可以表示为线性预测系数矩阵与冗余信号的乘积,即x=As,s称为x的线性预测稀疏表示.

2.2K-SVD算法

考虑x=Ds,s的稀疏性通过下式保证:

(7)

ε是最大误差.在D与s未知的情况下,式(7)可以等价地变形为:

(8)

图1　基于K-SVD算法和稀疏分解稀疏矩阵的稀疏线性预测字典训练示意图

稀疏字典D的初始化对于训练的结果具有影响,如前所说,采用线性预测矩阵初始化稀疏字典,而训练字典的长度(原子个数)设置4倍于语音帧长度N,即L=4N.需要注意的是K-SVD算法更新字典不是对整个字典一次性更新,而是每次只更新字典的一个原子,通过L次迭代或者达到收敛后完成字典学习[7].

3实验结果与分析

3.1基本实验设置

本节通过设计实验并分析实验结果来验证本文作者提出的SLPD在语音压缩感知重构中的有效性.实验语料采用NOIZEUS语料库[13],包含了干净语音和含噪语音.没有考察语音压缩感知的降噪性能,所以只用到了语料库中的干净语音部分.所有干净语音由30条短句组成,6个说话人,3男3女,每人5句,其中编号1～10和21～25由是男声,其余是女声.语音采样率8 kHz,2字节(16 bit)单通道.采用其中的20条作为训练用语音集,其余10条作为测试集.每个说话人随机选取3句作为训练样本,剩下的2句用于测试.总体实验框架分为3部分:SLPD训练、语音压缩感知处理和客观评价,实验的流程图如图2所示.

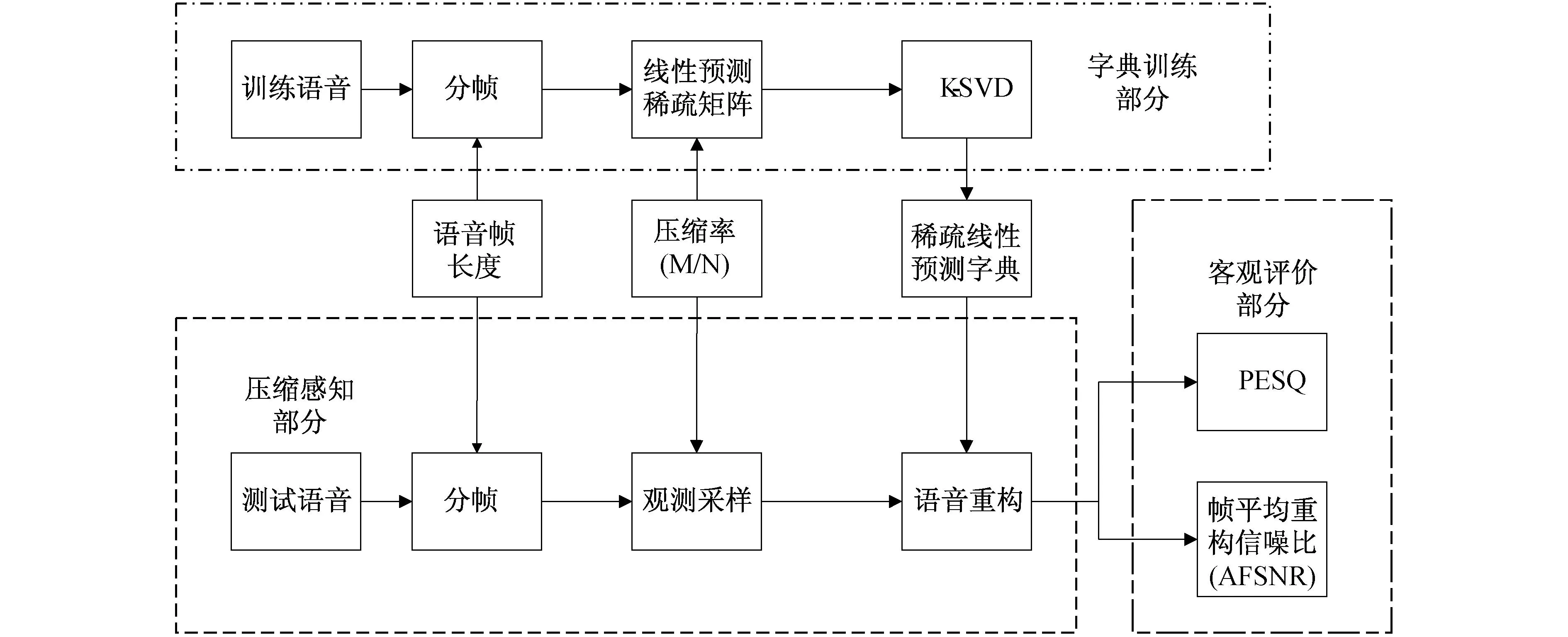
图2　基于稀疏线性预测字典的语音压缩感知实验流程图

从待处理语音信号帧的长度、压缩比、稀疏变换矩阵以及重构算法等因素从发,通过多个实验分析各参数对于压缩感知性能的影响.表1设置了本实验中涉及到参数.

表1　全局实验参数

帧平均信噪比(AFSNR)的定义如下:

经过数十年的外科技术发展，多种手术方式被应用于半椎体畸形的治疗中，包括前后联合入路内固定技术、凹侧松解前后联合入路矫形内固定技术、前后联合入路半椎体切除术以及单纯后路半椎体切除术等。在成人和儿童患者中，后路椎弓根螺钉的安全性和有效性均被证实［10-11］，但对颈椎半椎体畸形的固定效果尚无定论。2005年，Ruf等［1］提出，由于颈椎区域解剖结构的复杂性，应采取前后联合入路半椎体完全切除以获得最大程度的矫形效果。本例患者亦采取前后联合入路半椎体完全切除的方式，并进行了长节段的融合固定，以防止患者在术后出现脊柱整体失衡或局部代偿弯形成，术前对椎动脉位置也作了充分评估，减少了手术误伤。

(9)

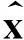
3.2实验结果与分析

实验一将SLPD和OMP重构算法用于语音压缩感知框架,验证SLPD在压缩感知重构中的有效性.图3所示是语音压缩感知重构效果图,压缩比为0.3,SLPD的字典大小为256×1024.(a)表示原语音;(b)是原语音区间1000到6120的放大部分,以显示更多的重构细节;(c)和(d)是相应的重构语音段.实验表明,将SLPD作为稀疏字典可以准确地恢复出原始语音信号而不丢失主要信息.

图3　语音压缩感知重构效果图(SLPD+OMP)

为了考察压缩比和语音帧长度对重构性能的影响,不改变实验一中的稀疏字典类型和重构算法,实验二分别对3类语音帧长度和5个压缩比进行了表1中的设置,采用AFSNR作为评价语音重构的性能指标,单位为dB.实验结果如表2所示.一方面,从表2的行来看,固定语音帧长度和字典大小,随着压缩比的增大,重构语音的AFSNR也增大;另一方面,从表2中每列的角度来看,固定压缩比,字典的大小也对重构性能有影响.字典越大,重构性能越好,AFSNR越大.

表2　SLPD联合OMP的语音压缩感知重构AFSNR

表3是采用CoSaMP重构算法重复实验二得到的重构语音信号的AFSNR.从表3可以看出,两种不同的算法的性能在语音压缩感知的应用方面相差无几,当压缩比为0.4和0.5时,OMP算法的重构效果略优于CoSaMP算法;当压缩比较小时,CoSaMP算法的重构性能则略优于OMP算法.

表3　SLPD联合CoSaMP的语音压缩感知重构AFSNR

图4　基于不同稀疏字典的压缩感知重构比较图

为了比较稀疏线性预测字典与传统解析字典在语音压缩感知重构中的性能,实验三分别采用了不同的稀疏字典用于语音信号的压缩感知重构,如表1所述,解析字典采用DCT字典,语音帧的长度为512,字典大小为(512,2048),重构效果比较图如图4所示.

图4中的4条曲线分别表示正交匹配追踪算法结合稀疏线性预测字典(OMP+SLPD,星号实线)、正交匹配追踪算法结合离散余弦变换字典(OMP+DCT,菱形虚线)、压缩采样匹配追踪算法结合稀疏线性预测字典(CoSaMP+SLPD,乘号实线)以及压缩采样匹配追踪算法结合离散余弦变换字典(CoSaMP+DCT,方形虚线).即虚线表示的是稀疏方式采用DCT字典,而实线则是表示采用SLPD.从图4中可以看出,采用SLPD的重构效果要高于DCT字典,效果提升约为0.6 dB左右.OMP+SLPD在压缩比为0.4和0.5时候效果优于CoSaMP+SLPD,而OMP+DCT在压缩比为0.4和0.5时候效果优于CoSaMP+DCT.

4结论

本文作者首先介绍了压缩感知的基本原理,并将压缩感知理论应用于语音信号的采样和压缩.重点研究了语音信号的稀疏性,从稀疏线性预测系数出发,采用K-SVD算法对语音训练集进行学习,构造稀疏线性预测字典,用于语音信号的稀疏分解.最后通过OMP和CoSaMP算法将已采样压缩的语音信号进行了逐帧重构,采用AFSNR作为语音重构的评价标准.在实验阶段考察了待处理语音信号帧的长度、压缩比、稀疏变换矩阵以及压缩感知重构算法等因素对压缩感知性能的影响,得出结论:(1)在相同压缩比条件下,重构效果随着稀疏字典大小(即语音帧长度)的增大而提高;(2)在字典大小相同的条件下,压缩比越大,重构效果越好;(3)相同重构算法情况下,采用SLPD作为稀疏字典的重构性能与采用DCT字典相比,SLPD能提高大约0.6 dB的重构AFSNR.初步研究了通过训练信号或数据集学习来的过完备字典在压缩感知中的应用,提高了传统的基于解析构造的字典的压缩感知性能,后续应该对压缩感知框架中重构算法的重构效率和观测矩阵与稀疏矩阵的RIP性质进行更深入的研究.

参考文献:

[1]Donoho D L.Compressed Sensing [J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[2]Candès E J,Romberg J K,Tao T.Stable signal recovery from incomplete and inaccurate measurements [J].Communications on Pure & Applied Mathematics,2006,59(8):1207-1223.

[3]Baraniuk R G.Compressive Sensing [Lecture Notes] [J].IEEE Signal Processing Magazine,2007,24(4):118-121.

[4]Christensen M G,Stergaard J,Jensen S H.On compressed sensing and its application to speech and audio signals[C]//IEEE.Signals,Systems and Computers,2009 Conference Record of the Forty-Third Asilomar Conference on,2009:356-360.

[5]Kassim L A,Gunawan T S,Khalifa O O,et al.Development of Low Bit Rate Speech Encoder based on Vector Quantization and Compressive Sensing [J].Journal of Applied Sciences,2013,13(1):49-59.

[6]Zhang C Q,Chen Y P,Tan W.Discrete Cosine Wavelet Packet Transform and Its Application in Compressed Sensing for Speech Signal[C]//IEEE.2012 Fourth International Symposium on Information Science & Engineering.Shanghai:IEEE,2012.

[7]Lian Q S,Shi B S,Chen S Z.Research Advances on Dictionary Learning Models,Algorithms and Applications [J].Acta Automatica Sinica,2015,41(2):240-260.

[8]Giacobello D,Christensen M G,Murthi M N,et al.Retrieving Sparse Patterns Using a Compressed Sensing Framework:Applications to Speech Coding Based on Sparse Linear Prediction [J].Signal Processing Letters IEEE,2010,17(1):103-106.

[9]Sun L H,Yang Z,Ji Y Y,et al.Reconstruction of compressed speech sensing based on overcomplete linear prediction dictionary [J].Chinese Journal of Scientific Instrument,2012,33(4):743-749.

[10]Li Y,Li S T.Speech Recovery Model and Algorithm over Sparse Representation based on Compressive Sensing [J].Journal of Signal Processing,2014(8):914-923.

[11]Shi G M,Liu D H,Gao D H.Advances in Theory and Application of Compressed Sensing [J].ACTA Electronica Sinica,2009,37(5):1070-1081.

[12]Rubinstein R,Faktor T,Elad M.K-SVD dictionary-learning for the analysis sparse model[C]//IEEE.Acoustics,Speech and Signal Processing (ICASSP),2012 IEEE International Conference on.Kyoto:IEEE,2012.

[13]Hu Y,Loizou P C.Subjective comparison and evaluation of speech enhancement algorithms [J].Speech Communication,2007,49(49):588-601.

(责任编辑：包震宇)

The application of sparse linear prediction dictionary tocompressive sensing in speech signals

YOU Hanxu, LI Wei, LI Xin, ZHU Jie

(School of Electronic Information and Electrical Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Abstract:Appling compressive sensing (CS),which theoretically guarantees that signal sampling and signal compression can be achieved simultaneously,into audio and speech signal processing is one of the most popular research topics in recent years.In this paper,K-SVD algorithm was employed to learn a sparse linear prediction dictionary regarding as the sparse basis of underlying speech signals.Compressed signals was obtained by applying random Gaussian matrix to sample original speech frames.Orthogonal matching pursuit (OMP) and compressive sampling matching pursuit (CoSaMP) were adopted to recovery original signals from compressed one.Numbers of experiments were carried out to investigate the impact of speech frames length,compression ratios,sparse basis and reconstruction algorithms on CS performance.Results show that sparse linear prediction dictionary can advance the performance of speech signals reconstruction compared with discrete cosine transform (DCT) matrix.

Key words:compressive sensing; audio and speech signal processing; K-SVD; spare linear prediction dictionary

中图分类号:TN 912

文献标志码:A

文章编号:1000-5137(2016)02-0223-07

通信作者:朱杰,中国上海市闵行区东川路800号,上海交通大学电子信息与电气工程学院,邮编:200240,E-mail:zhujie@sjtu.edu.cn

基金项目:国家自然科学基金(61271349,61371147,11433002);上海交通大学医工合作基金(YG2012ZD04)

收稿日期:2016-02-29