基于测距的定位系统中位置解算研究

刘中令, 徐超杰, 俞　晖

(上海交通大学 电子信息与电气工程学院,上海 200240)



基于测距的定位系统中位置解算研究

刘中令, 徐超杰, 俞晖

(上海交通大学 电子信息与电气工程学院,上海 200240)

摘要:在现有的基于测距的位置解算算法中,定位精度受测距误差的影响较大.为了提高定位精度,提出了一种基于根心的位置解算算法.该算法中,首先根据位置未知的节点(Target节点)与每三个位置已知的节点(Anchor节点)之间的距离测量值,计算出对应的根心坐标;在根心集合中,滤除误差较大的部分根心;根据剩余根心的坐标及其权重值,计算平均值作为解算结果.仿真结果表明,在相同的误差下,提出的位置解算算法相比于现有的基于测距的位置解算算法有效地降低了解算误差,提高了定位精度.

关键词:位置解算算法; 根心; Anchor节点; Target节点

0概述

随着GPS系统、北斗系统以及伽利略系统等卫星系统基本解决室外定位的问题,越来越多的人开始关注室内定位.但是,由于卫星信号在室内衰减非常严重,同时室内环境复杂,对卫星信号有很大的干扰,所以通过卫星信号定位的方法不适于室内情况.然而随着通信技术、互联网技术的高速发展,国内外的研究者提出了很多基于短距离无线通信技术的定位方法,比如:WiFi[1]、蓝牙[2]、Zigbee[3]、超宽带[4](UWB)等,并且精度也在日渐提高.

在众多室内定位方法中,位置解算算法主要分为两种算法:Range-free和Range-based.Range-free算法通过测量信号的Received Signal Strength Indication(RSSI)来估计被测物体位置,以基于WiFi的定位方法为代表.虽然定位精度无法很高,但使用WiFi的设备十分普遍,所以这种方法很受欢迎.Range-based算法是测量位置已知的节点和位置未知的节点之间的距离、角度或距离差,计算位置未知的节点相对位置已知的节点的坐标,从而得到位置未知的节点的位置信息.近几年,随着UWB技术被引入室内定位,测量的距离的精度可以达到分米级甚至厘米级,Range-based算法的定位精度已经可以做到很高,同时由于算法容易编程实现,所以Range-based算法也十分受青睐,不过,Range-based算法对硬件设备的要求比Range-free算法更高.

本文作者将介绍一种基于根心的Range-based算法,并通过Matlab仿真实验,将本文作者提出的算法与已有的Range-based定位解算算法进行对比,观察算法性能.

1基本算法介绍

1.1经典算法介绍

设位置已知的节点(Anchor节点)坐标分别为(x1,y1)、(x2,y2)、…、(xn,yn),测量的位置未知的节点(Target节点)到各个位置已知的节点的距离分别为d1、d2、…、dn.两种经典的算法如下.

1.1.1三边测量法

选取3个Anchor节点,其坐标为(x1,y1)、(x2,y2)、(x3,y3),测量的Target节点到这3个Anchor节点之间的距离分别为d1、d2、d3,设Target节点坐标为(x,y),可以得到表达式:

(1)

将式(1)化简,可得:

(2)

求解式(2),即可得到三边测量法的定位解算结果.

1.1.2极大似然估计法

选取n个Anchor节点,可以得到表达式:

(3)

将式(3)化简,可得:

(4)

将式(4)写成矩阵的形式,即AX=b,其中:

极大似然估计法的解算结果为:

(5)

1.2根心介绍

1.2.1根心定理

定义1点对圆的幂:平面上一点P(x,y)对一个圆心为O(x0,y0),半径为r的圆的幂为:

定义2根轴:对平面式2个不同心的圆等幂的点集称为根轴.

根据上述定义,可以计算出2个不同心的圆的根轴.设2个不同心的圆的圆心分别为(x1,y1)、(x2,y2),半径分别为r1、r2,这2个圆的根轴的表达式为:

定理1根心定理(蒙日定理):平面上任意3个圆,若这3个圆圆心不共线,则3条根轴相交于一点,这个点叫它们的根心;若3圆圆心共线,则3条根轴互相平行.

1.2.2计算根心

设3个两两不同心的圆的圆心分别为(x1,y1)、(x2,y2)、(x3,y3),半径分别为r1、r2、r3,根据定义2可以得到3条根轴的表达式:

(6)

假设3条根轴两两相交,根据定理1,则3条根轴必相交于一点,所以,选取式(1)中的前两个方程,可得:

(7)

根据克莱姆法则,可以计算出根心坐标:

(8)

2算法改进

2.1算法模型

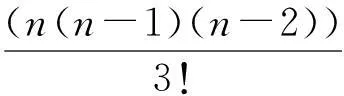
2.2选取根心坐标

设3个圆心不共线的圆,其圆心分别为O1、O2、O3,半径分别为r1、r2、r3,这3个圆在平面上的相交情况有以下几种情况:

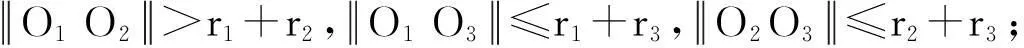
如图1所示.

图1　平面上3个圆相交的情况示意图

根据根心定理,由于3个圆的圆心不共线,可知以上4种情况,根心都必定存在,以图1(1)为例,根心如图2所示.

图2　根心示意图

设计算出的根心为P(xp,yp),圆Oi(圆心为Oi(xi,yi),半径为ri,i=1,2,3)与射线OiP相交于点Qi,可以得到Qi的坐标为:

(9)

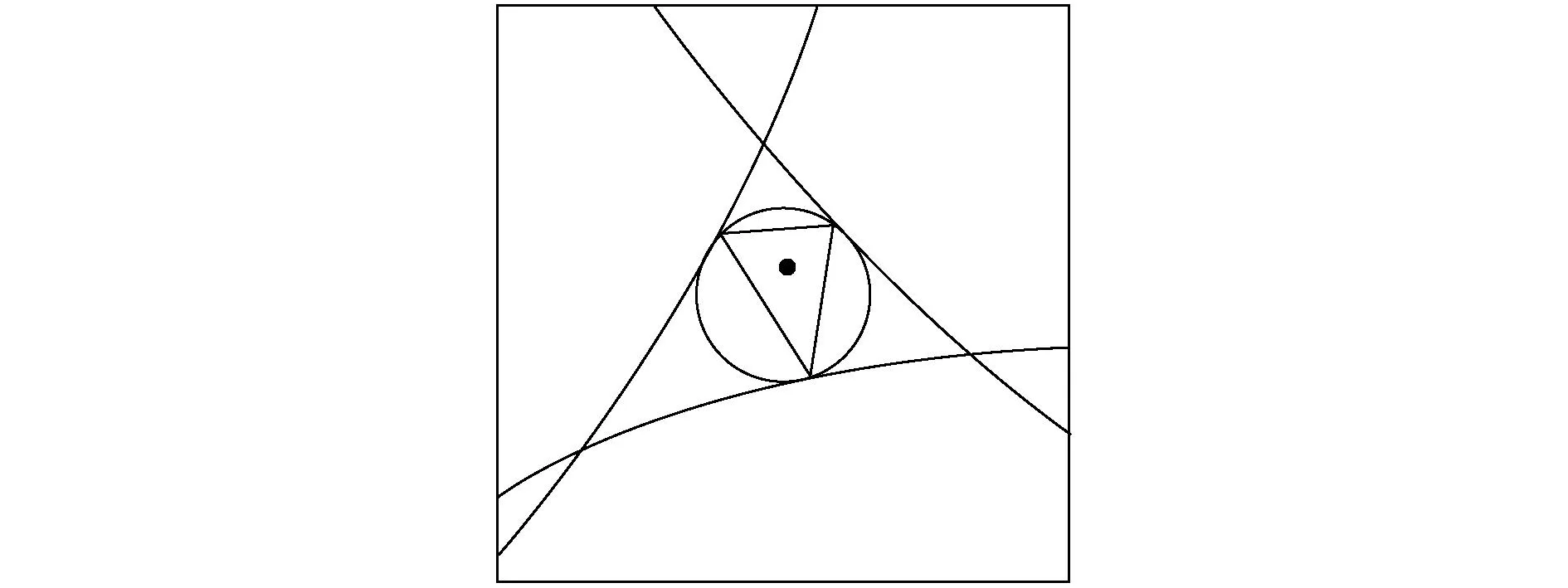
图3　交点构成的三角形及其外接圆示意图

由3个圆的圆心坐标和半径可以算出3个交点坐标,再根据这3个交点坐标,可以得到一个以这3个交点为顶点的三角形以及三角形的外接圆,如图3所示.

在定位算法中,圆心坐标为Anchor节点的坐标,圆的半径为测距值,可以由式(8)得到根心坐标,由式(9)得到3个交点的坐标.经过仿真实验,3个交点构成的三角形面积与三角形外接圆半径之比和定位解算精度成正相关,所以,认为交点构成的三角形面积与三角形外接圆半径之比越大,所对应的根心坐标误差越小.

2.3算法流程

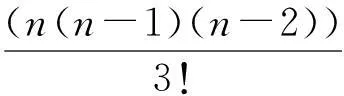
第二步:根据式(9)计算出以Anchor节点为圆心Oi(xi,yi)、Anchor节点与Target节点间的测距值为半径ri的圆与射线OiP的交点Qi(xQi,yQi).

第三步:由3个交点Q1、Q2、Q3可以围成一个三角形和三角形的外接圆,计算三角形面积S和外接圆半径r.

3仿真结果及分析

3.1仿真实验

本文作者提出了一种基于根心的位置解算算法,为了评估算法性能,采用Matlab进行实验仿真,并与其他几种算法进行对比,观察提出的算法的优化幅度.从文献[5]中可知,在视距情况下,测距误差的分布呈高斯分布,所以仿真实验中所加噪声为高斯噪声.仿真实验的相关参数如下:假设定位范围是20m×20m,Anchor节点的总数量为10个,Anchor节点彼此之间都可以通信并且不存在3个共线的Anchor节点,Target节点的数量为1个,Target节点与Anchor节点之间的距离加上高斯噪声作为测量值,通过更改测距误差最大值观察算法性能.

评估算法性能使用如下的定位误差公式:

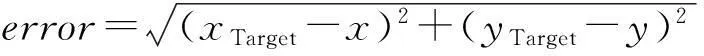
(10)

其中,(xTarget,yTarget)为Target节点的实际坐标,(x,y)为解算坐标.式(10)表示的是解算出的坐标与Target节点实际坐标之间的距离.

仿真实验中使用的算法包括:极大似然估计法[6]:使用10个Anchor节点的坐标和10个Anchor节点与Target节点之间的测距值,由式(5)计算出解算坐标;文献[7]中的基于根心的位置解算算法(以下简称根心法);优化算法:保留较大的10%的W值对应的根心坐标,求其加权平均值作为解算结果.

3.2实验结果分析

基于3.1中的仿真环境,本实验对上述3种算法:极大似然估计法、根心法以及优化算法进行仿真,结果如图4所示.

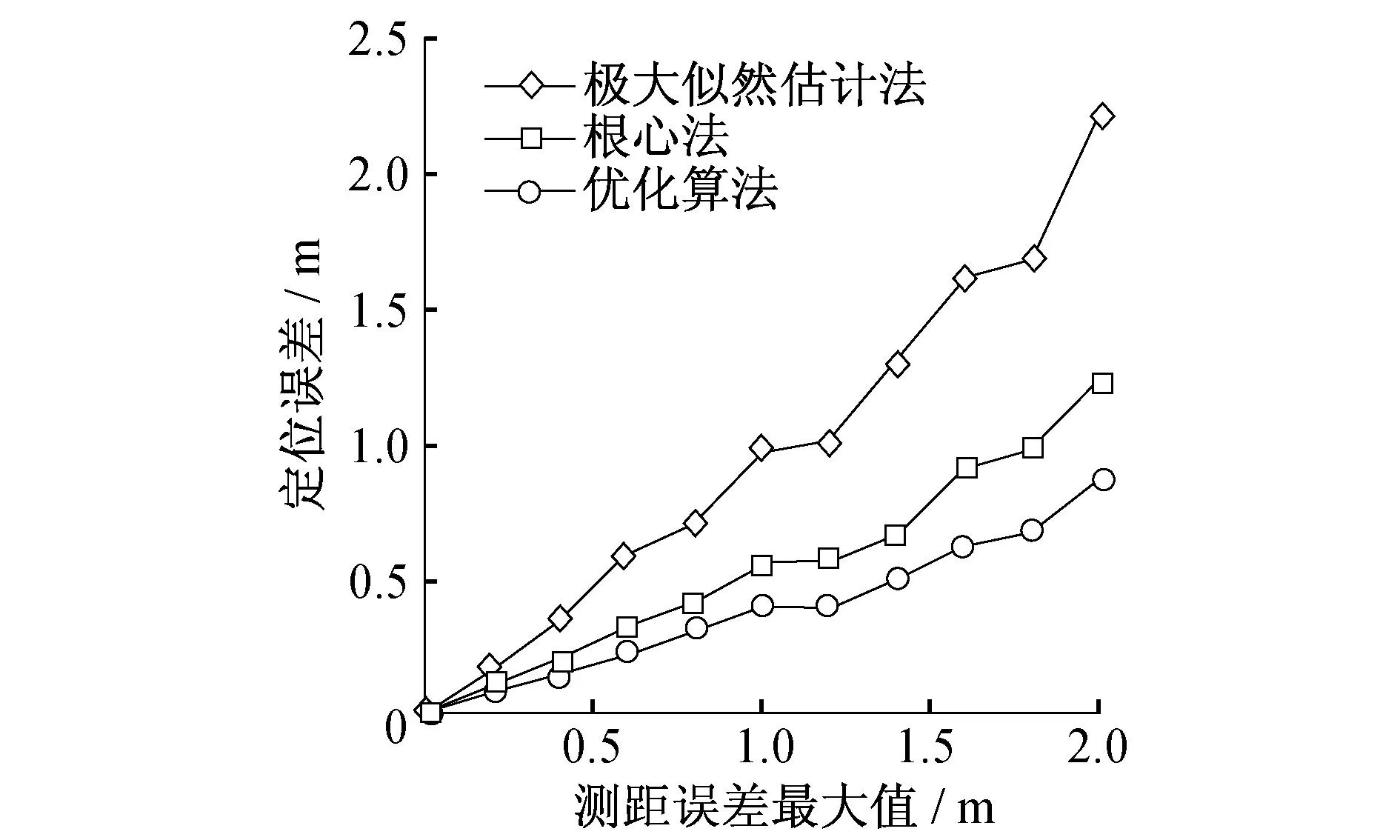
图4　仿真结果

如图4仿真结果所示,测距误差最大值由0 m增大至2 m.从图4中可以看出,优化算法相比极大似然估计法有了显著提高,通过计算,定位精度提高了60%;相比根心法,优化算法也有明显提高,通过计算,定位精度提高了28%.同时,是仿真实验中,优化算法的定位误差始终小于1 m,定位精度可以达到分米级,可见优化算法的改进幅度很大.

4结束语

本文作者研究了一种基于根心的位置解算算法:将Anchor节点每三个一组,计算出对应的根心坐标;计算3个圆心到根心的射线与圆的交点,可以得到一个以3个交点为顶点的三角形以及三角形的外接圆;计算三角形面积与外接圆半径之比,将其作为权值;保留较大权值对应的根心坐标,求其平均值作为解算结果.通过仿真实验,本文作者将优化算法与极大似然估计法、文献[7]中的根心法进行对比,实验结果表明,优化算法相比上述两种算法有了很大改善,定位精度有显著提高.

参考文献:

[1]Niu J W,Wang B W,Cheng L,et al.WicLoc:an indoor localization system based on WiFi fingerprints and crowdsourcing [C]//IEEE.2015 IEEE International Conference on Communications(ICC).London:IEEE,2015.

[2]Oksar I.A Bluetooth signal strength based indoor localization method [C]//IEEE.2014 International Conference on Systems,Signals and Image Processing(IWSSIP).Dubrovnik:IEEE,2014.

[3]Hu X,Cheng L L,Zhang G C.A Zigbee-based localization algorithm for indoor environments [C]//IEEE.2011 International Conference on Computer Science and Network Technology(ICCSNT).Harbin:IEEE,2011.

[4]Irahhauten Z,Nikookar H,Klepper M.A joint ToA/DoA technique for 2D/3D UWB localization in indoor multipath environment [C]//IEEE.2012 IEEE International Conference on Communications(ICC).Ottawa:IEEE,2012.

[5]Chehri A,Fortier P,Tardif P M.UWB-based sensor networks for localization in mining environments [J].Ad Hoc Networks,2009,7(5):987-1000.

[6]Huang Y F,Jheng Y T,Chen H C.Performance of an MMSE based indoor localization with wireless sensor networks [C]//IEEE.2010 Sixth International Conference on Networked Computing and Advanced Information Management(NCM).Seoul:IEEE,2010.

[7]Chen Y S,Chin C C,Deng D J.Efficient localization algorithm in wireless ad hoc sensor networks by utilizing radical centers [C]//IEEE.2012 IEEE International Conference on Communications(ICC).Ottawa:IEEE,2012.

(责任编辑：顾浩然)

Study on position computing in range-based localization system

LIU Zhongling, XU Chaojie, YU Hui

(School of Electronic Information and Electrical Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Abstract:In the existing range-based position computing algorithm,the localization accuracy is greatly influenced by the error of measured distance.In order to improve the localization accuracy,this paper presents an optimized indoor localization algorithm based on radical center.In the algorithm,firstly,calculating the radical center bases on the measured distance between every three anchor nodes and the target node.Then,percentage of the radical centers in the set which have large localization error are filtered out.Finally,computing the average of the remaining radical centers′ coordinates as the result bases on their weight.The result of simulation showed that compared with the existing range-based position computing algorithm,the presented position computing algorithm reduces the localization error and improves the localization accuracy effectively.

Key words:position computing algorithm; radical center; anchor node; target node

中图分类号:TN 929.5

文献标志码:A

文章编号:1000-5137(2016)02-0209-06

通信作者:俞晖,中国上海市闵行区东川路800号,上海交通大学电子信息与电气工程学院,邮编:200240,E-mail:yuhui@sjtu.edu.cn.

收稿日期:2016-03-04